Time, Speed, Distance and concept of proportionality: Questions, Examples

In the realm of physics and mathematics, understanding the concepts of Time, Speed, and Distance is fundamental. These concepts are not only essential for solving academic problems but also have practical applications in daily life, such as travelling, athletics, and planning. We will also explore the introduction to time management, which is crucial for effectively organizing and planning tasks to optimize productivity. Additionally, we will touch on the introduction to time series analysis and the introduction to time series data, which are vital in analyzing and forecasting data points collected or recorded at specific time intervals. This article will delve into these core concepts, ‘introduction to speed distance time’, ‘what is the relationship between speed distance and time’, illustrating their interrelationships, units of measurement, and practical applications.

Speed, Distance, and Time: Concept

Definition

• Distance: The total path covered by an object during motion.

• Time: The duration taken to cover a certain distance.

• Speed: The rate at which an object covers distance.

Example

Suppose a car is travelling from City A to City B, which is 60 kilometres apart. If the car travels at 60 km/hr speed, then it will take 1 hour to cover this distance.

Illustration

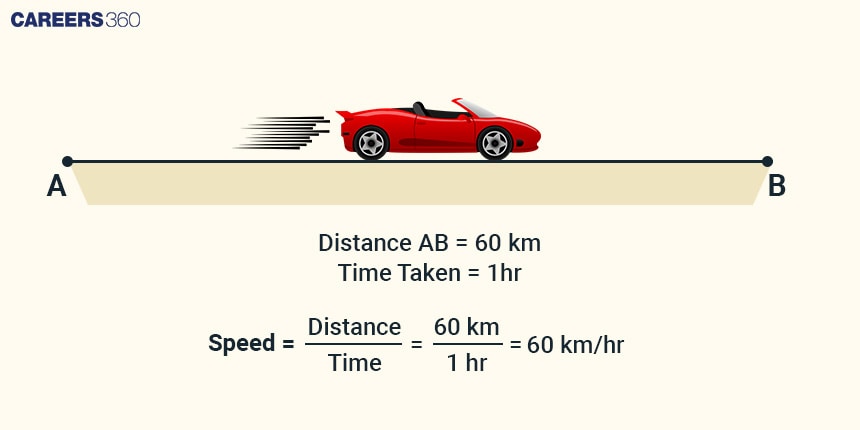Relation between Speed, Distance, and Time

The relationship between speed, distance, and time is crucial for solving problems. These relationships can be expressed using the following formulas:

Any basic problems related to Time, Speed, and Distance can be solved by using these formulas. However, the correct usage of units is also an important thing to consider while using formulas.

Units of Speed, distance, and time

Conversion from km/hr to m/s

To convert km/hr to m/s, we need to convert the kilometre to metre and hour to seconds.

1 km/hr = $\frac{\text{1 km}}{\text{1 hr}}$ = $\frac{\text{1000 m}}{\text{3600 s}}$ = $\frac{5}{18}$ m/s

We can also write it as, 1 km/hr = $\frac{1}{3.6}$ m/s

Conversion from m/s to km/hr

To convert m/s to km/hr, we need to convert the metre to kilometre and to second to hour.

1 m/s = $\frac{\text{1 m}}{\text{1 s}}$ = $\frac{\frac{1}{1000} km}{\frac{1}{36000} hr}$ = $\frac{18}{5}$ km/hr

We can also write it as, 1 m/s = 3.6 km/hr

Concept of proportionality:

Proportionality helps us understand how one quantity changes with respect to another. In the context of time, speed, and distance we often deal with direct and inverse variations.

Direct Variation of Distance with Speed

When time is constant, the distance travelled is directly proportional to the speed.

So, Distance ∝ Speed (when Time is constant)

Example: A car covers a distance of 100 km at some time at 25 km/hr speed.

Now at 50 km/hr, the car will cover (100 × 2) = 200 km at the same time.

Therefore, if we increase the speed at the same time, we can cover more distance.

Direct Variation of Distance with Time

When the speed is constant, the distance travelled is directly proportional to time.

So, Distance ∝ Time (when Speed is constant)

Example: A car covers a distance of 100 km in 2 hours at a constant speed.

Now in 4 hours, the car will cover (100 × 2) = 200 km at the same speed.

Therefore, if we increase the time at the same speed, we can cover more distance.

Indirect Variation of Speed with Time

When the distance is constant, the speed is inversely proportional to the time taken.

So, Speed ∝ $\frac{1}{\text{Time}}$

Example: A journey of some certain distance takes 3 hours at a speed of 40 km/hr. If we need to reduce the time to 2 hours, then the speed will have to $\frac{40×3}{2}$ = 60 km/hr.

Therefore, if we decrease the time for the same distance, then the speed will increase.

Tips and Tricks

• Understand the basic formulas of time, speed and distance and their interrelation.

• Always convert all units to a consistent set before solving a problem. For instance, if the distance is in kilometres and time is in hours, ensure the speed is in km/hr.

• The formula for average speed when travelling different distances at different speeds is:

Average speed = $\frac{\text{Total distance}}{\text{Total time}}$.

• When two objects are moving in the same direction, the relative speed is the difference in their speeds.

• When two objects are moving in opposite directions, the relative speed is the sum of their speeds.

• For more information on the concept of Average speed and Relative speed click here.

• For more information on the application of Time, speed, and distance in problems on trains click here.

• For more information on the application of Time, speed, and distance in the problems of boat and stream click here.

Practice Questions/Solved Examples

Q.1.

A man travels $\frac{3}{4}$th of the distance of his journey by bus, $\frac{1}{6}$th by rickshaw, and the remaining 2 km on foot. The total distance travelled by the man is:

1. 12 km

2. 18 km

3. 20 km

4. 24 km

Hint: Let the total distance be $x$ km. Find the remaining distance and equate it with 2 km.

Solution:

Given: A man travelled by bus $\frac{3}{4}$th of the total distance.

The man travelled by rickshaw $\frac{1}{6}$th of the total distance.

The man travelled on foot = 2 km

Let the total distance to be $x$ km.

So, the remaining distance $=x-\frac{3x}{4}-\frac{x}{6}$

According to the question,

$x-\frac{3x}{4}-\frac{x}{6} = 2$

$⇒\frac{12x-9x-2x}{12}=2$

$⇒\frac{x}{12}=2$

$\therefore x=24$

Hence, the correct answer is option (4).

Q.2.

To cover a certain distance at a speed of 60 km/hr, a train takes 15 hours. If it covers the same distance in 12 hours, what will its speed be?

1. 65 km/hr

2. 70 km/hr

3. 75 km/hr

4. 80 km/hr

Hint: Use the formula of Distance = Speed × Time.

Solution:

Given: A train takes 15 hours to cover a certain distance at a speed of 60 km/hr.

Distance = Speed × Time = 15 × 60 = 900 km

$\therefore$ Required speed to cover this distance in 12 hours = $\frac{900}{12}$ = 75 km/hr

Hence, the correct answer is option (3).

Q.3.

Sound travels at 330 metres per second. The distance (in kilometres) of a thundercloud when it’s sound follows the flash after 10 seconds is:

1. 0.33 km

2. 3.3 km

3. 33 km

4. 33.3 km

Hint: Use the formula below to solve it.

Distance = Speed × Time

Solution:

Given: The speed of sound is 330 metres/second.

We know,

Distance = Speed × Time

= (330 × 10) metres

= 3300 metres

= 3.3 km

Hence, the correct answer is option (2).

Q.4.

At an average speed of 80 km/hr, the Shatabdi Express reaches Ranchi from Kolkata in 7 hours. The distance between Kolkata and Ranchi is:

1. 506 km

2. 560 km

3. 506 m

4. 650 m

Hint: Use this formula: Distance = Average speed × Time

Solution:

Given:

The average speed = 80 km/hr

Time = 7 hours

Distance = Average speed × Time = 80 × 7 = 560 km

Hence, the correct answer is option (2).

Q.5.

A truck covers a distance of 550 metres in one minute whereas a bus covers a distance of 33 km in $\frac{3}{4}$ hour. Then the ratio of their speeds is:

1. $1:2$

2. $2:3$

3. $3:4$

4. $4:5$

Hint: Use the formula: Speed = $\frac{\text{Distance}}{\text{Time}}$

Solution:

Given:

The truck covers a distance of 550 metres in one minute.

The bus covers a distance of 33 km in $\frac{3}{4}$ hour.

Speed of the truck in metres per second = $\frac{550}{1×60}$ = $\frac{55}{6}$

Speed of the bus in metres per second = $\frac{33×1000}{\frac{3}{4}×60×60}$ = $\frac{33×1000}{45×60}$ = $\frac{110}{9}$

Required ratio = $\frac{\text{Speed of truck}}{\text{Speed of bus}}$

= $\frac{\frac{55}{6}}{\frac{110}{9}}$

= $\frac{55}{6}×\frac{9}{110}$

= $\frac{3}{4}$

= $3:4$

Hence, the correct answer is option (3).

Q.6.

Rameshwar goes on a trip on his motorcycle and rides for 405 kilometres. If he rides for 6 hours at a speed of 45 km/hr, find at what speed he travels for the remaining 3 hours of the journey.

1. 55 km/hr

2. 52 km/hr

3. 45 km/hr

4. 40 km/hr

Hint: Use the formula: $\text{Speed} = \frac{\text{Distance}}{\text{Time}}$

Solution:

Given: Total distance covered = 405 km

He rides for 6 hours at a speed of 45 km/hr.

Distance covered in 6 hours = 6 × 45 = 270 km

Distance left = 405 – 270 = 135 km

So, his speed for the remaining 3 hours of the journey = $\frac{135}{3}$ = 45 km/hr

Hence, the correct answer is option (3).

Q.7.

If a train maintains an average speed of 42 km/hr, it arrives at its destination at the right time. If however, the average speed is 40 km/hr, it arrives 15 minutes late. Find the distance of the journey.

1. 210 km

2. 209 km

3. 205 km

4. 200 km

Hint: Use this formula:

Distance = Speed × Time

Solution:

Let the time be $x$ hours when the train moves at a speed of 42 km/hr.

So, time will be $(x+\frac{1}{4})$ hours when the train moves at a speed of 40 km/hr.

(15 minutes = $\frac{1}{4}$ hour)

Distance = Speed × Time

$⇒42×x = 40 × (x+\frac{1}{4})$

$⇒2x=10$

$\therefore x=5$

Total distance = 42 × 5 = 210 km

Hence, the correct answer is option (1).

Q.8.

The speeds of the three cars are in the ratio of $1:3:5$. The ratio of the time taken by these cars to travel the same distance is _____.

1. $3:5:15$

2. $15:3:5$

3. $15:5:3$

4. $5:3:1$

Hint: Time is inversely proportional to the speed.

$\text{Time} \propto \frac{1}{\text{Speed}}$

Solution:

We know, $\text{Time} \propto \frac{1}{\text{Speed}}$

Required ratio of time = $1:\frac{1}{3}:\frac{1}{5}$

L.C.M. of 1, 3, and 5 is 15.

= $1 × 15:\frac{1}{3}×15:\frac{1}{5}×15$

= $15:5:3$

Hence, the correct answer is option (3).

Q.9.

Anuj and Anup have to travel from place A to place B in their respective cars. Anuj is driving at 70 km/hr and takes 3 halts of 10 minutes each, while Anup is driving at 80 km/hr and takes 4 halts of 15 minutes each. The time taken by Anup to reach place B, if Anuj takes 8.5 hours, is:

1. 8 hours

2. 7 hours

3. 4 hours

4. 6 hours

Hint: Use this formula:

$\text{Speed} = \frac{\text{Distance}}{\text{Time}}$

Solution:

Given: Time spent by Anuj on halts = (10 × 3 = 30) minutes = 0.5 hours

Anuj's speed = 70 km/hr.

He travels for 8.5 – 0.5 = 8 hours

$\text{Speed} = \frac{\text{Distance}}{\text{Time}}$

So, place B's distance from A = 70 × 8 = 560 km

Time spent by Anup on halts = (15 × 4 = 60) mins = 1 hour

Anup's speed = 80 km/hr

Time taken to travel 560 km = $\frac{560}{80}$ = 7 hours

$\therefore$ The total time Anup takes is 7 + 1 = 8 hours

Hence, the correct answer is option (1).

Q.10.

Raghav covers a distance of 3300 m in 45 minutes. What is his speed (in km/hr)?

1. 5

2. 4.4

3. 3.75

4. 2.25

Hint: Use this formula:

$\text{Speed} = \frac{\text{Distance}}{\text{Time}}$

Solution:

Given:

Distance covered = 3300 m = $\frac{3300}{1000}$ = 3.3 km

Time taken = 45 minutes = $\frac{45}{60}$ = 0.75 hours

Speed = $\frac{\text{Distance}}{\text{Time}}$ = $\frac{3.3}{0.75}$ = 4.4 km/hr

Hence, the correct answer is option (2).