COS Full Form

In Mathematics, “Cos” refers to “Cosine”. In this article, You will get to learn about the theory and also its functionalities in trigonometry.

As such, you are acquainted with the “right-angled triangle” where you have the “mathematical terms” like hypotenuse, base, and height. Isn’t it right? We will take the help of a right-angled triangle to define cos but can apply the function of cos to any triangle for sure. Let us enter into the article to explore further.

What Is Trigonometry?

Trigonometry denotes the interesting branch of mathematics that focuses on the right-angled triangle to introduce and define the trigonometric terms and various associated components in its own domain.

What Are The Elements Of A Right-Angled Triangle?

The essential elements of trigonometry are defined as follows, taking the reference to the right-angled triangle.

The side that completes the right-angled triangle lying opposite to the right angle is named the hypotenuse.

Now, we know that a triangle has three angles. In a right-angled triangle, one angle is right angle and thus, the other two angles are acute-angled. To define the other two sides, we choose one of these angles as the reference angle.

The side of the right-angled triangle that encloses the reference angle along with the hypotenuse is designated as the base or the adjacent side.

The other side of the right-angled triangle opposite to the reference angle is called the perpendicular or the height or the opposite side. It is actually perpendicular drawn to the base of the right-angled triangle at its vertex.

What Is The Full Form Of “Cos”?

The full form of cos is the trigonometric term ‘cosine’. It is defined as the ratio of the base to the hypotenuse in the right-angled triangle. As such the base and the height can be interchangeably referred to which depends on our reference angle as we have discussed above.

Some Important Trigonometric Values In Cos Form

As such, you can find the value of cos of any angle defined in the equations, inequalities, identities, etc.

Here are some important trigonometric values in cos form.

• The value of cos 0 degrees is 1.

• The cos 30 degrees yields the value of 0.866.

• The estimate of cos 45 degrees is 0.707.

• The numerical value of cos 60 degrees equals 0.50

• The cos 90 degrees is equal to 0.

Some Worth Mentioning Points Of Trigonometry

Note the following important points in trigonometry.

• The trigonometric functions of cosine (cos) and sine (sin) are equal for angles complementary to each other.

• The other mutually complementary trigonometric functions are tangent (tan) and cotangent (cot); and secant and cosecant.

• There exist several trigonometric identities which hold good for every geometric shape where you can use the trigonometric functions as applicable or allowable.

Examples Of Trigonometric Function Cos

The following are examples where the trigonometric function cos is involved.

• The mathematical expressions \[2{{\cos }^{3}}\theta +a,\ \ {{\cos }^{2}}\frac{\pi }{2}+3\] 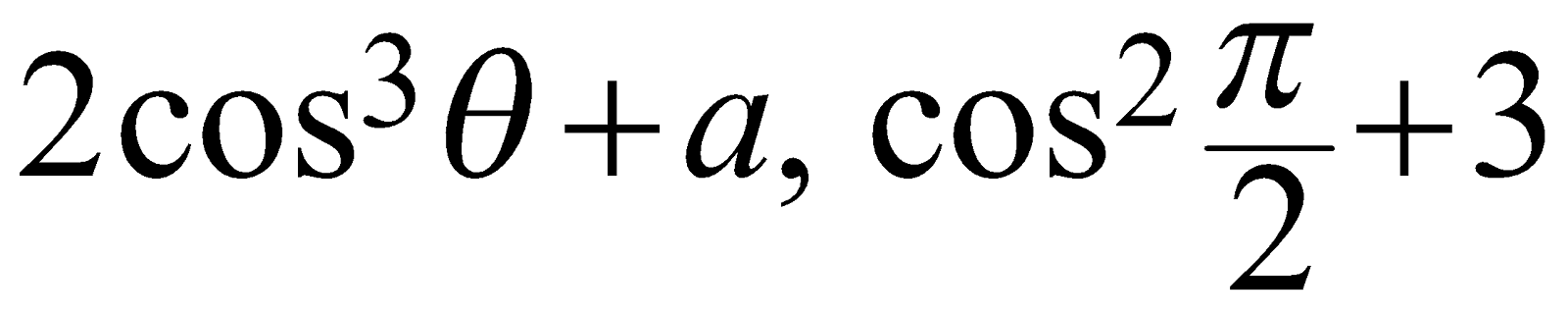are examples of the “trigonometric expressions” involving cos function.

• These mathematical Equations \[2{{\cos }^{3}}\theta +a=b,\ \ 4{{\cos }^{2}}\frac{\pi }{2}-1=\sin \alpha \] 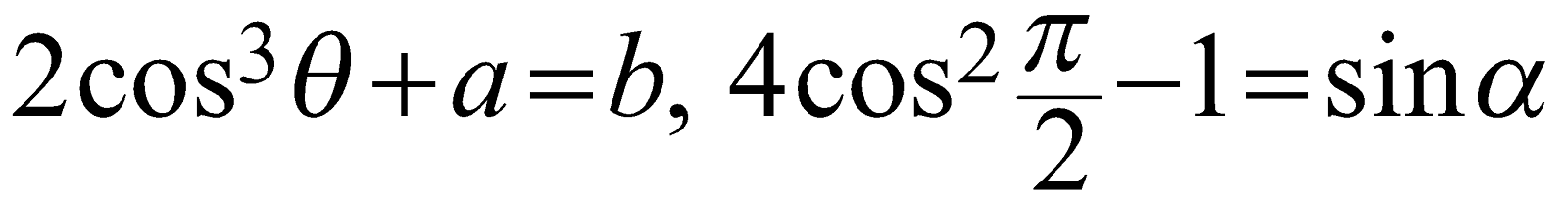are examples of the “trigonometric Equations”.

• The famous identity \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1 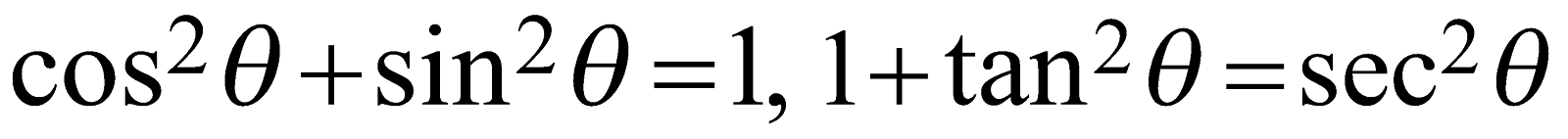is an example of the square trigonometric identity.

This identity \begin{align} \cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta \\ \end{align} 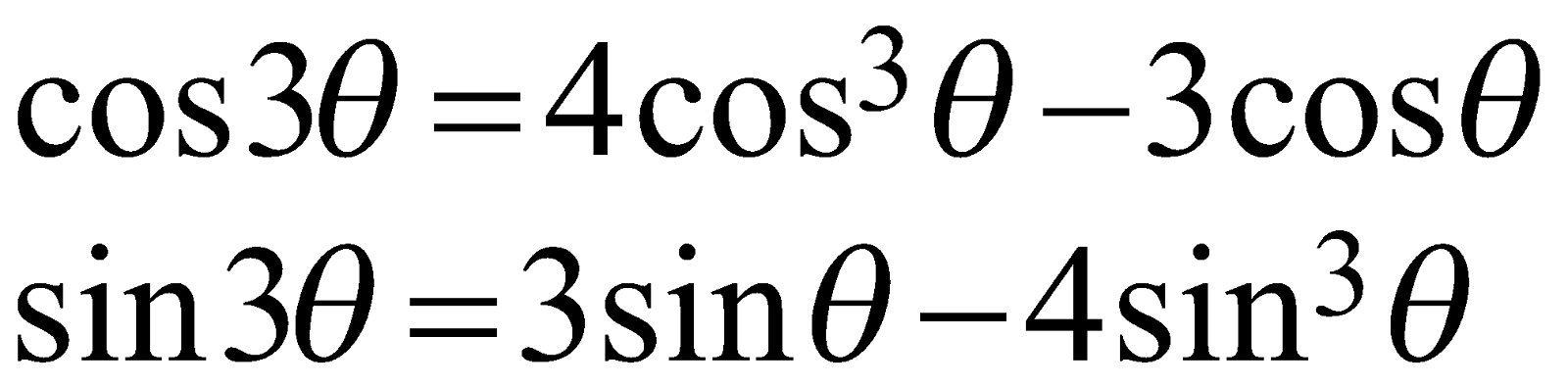is an example of the multiple angle trigonometric identity.