Algebraic Equations - Definition, Types, Formulas, Examples

Edited By Team Careers360 | Updated on Jul 02, 2025 05:15 PM IST

A mathematical statement in which two expressions are made equal to one another is known as an algebraic equation. A variable, coefficients, and constants are the typical components of an algebraic equation. Equations, or the equal sign, simply signify equality. The main purpose of equations is to equate two quantities. Equations act as a scale of balance. Anything on one side of the equal sign must have the same value on the opposite side for it not to be considered unequal. Because polynomials are included on both sides of the equal sign, algebraic equations are also referred to as polynomial equations. When a number or collection of numbers satisfies an algebraic equation, they are referred to as the equation's roots or solutions.

This Story also Contains

What Are Algebraic Equations?
What Is An Equation?
Types Of Algebraic Equations
What Is An Algebraic Expression?
Formulas For Algebraic Equations
How Are Algebraic Equations Solved?
Points To Remember

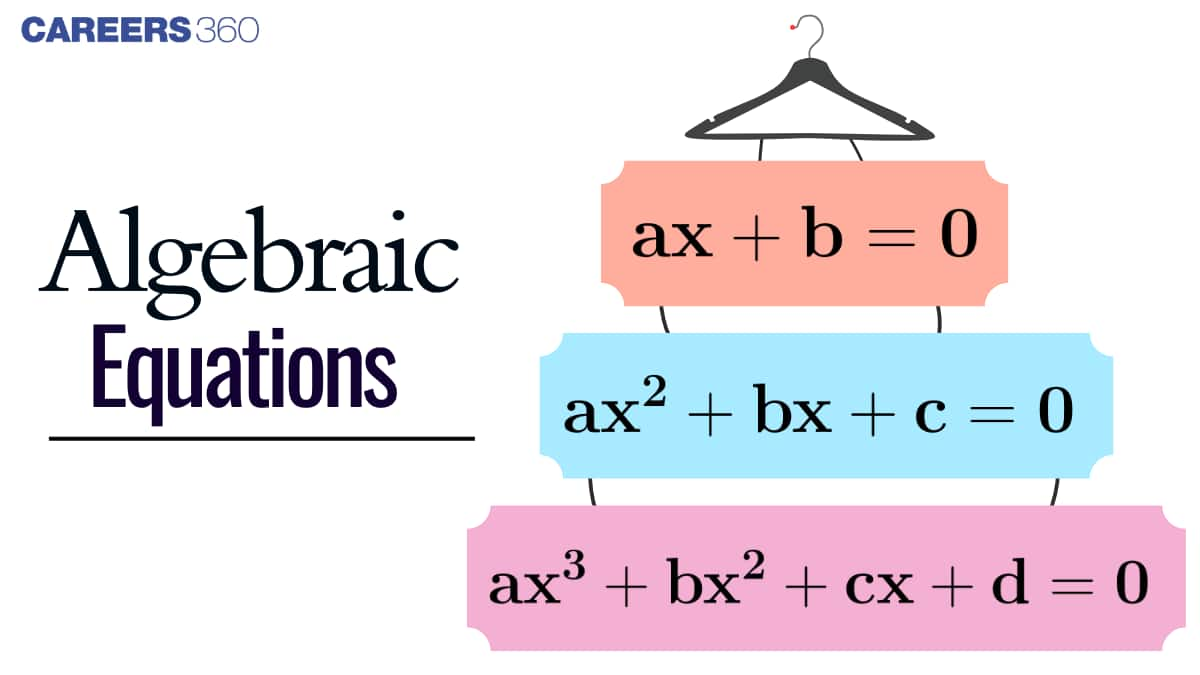
Algebraic Equations - Definition, Types, Formulas, Examples

What Are Algebraic Equations?

A balanced equation with variables, coefficients, and constants is what is known as an algebraic equation.

An equation with the following form is an algebraic equation:

Q = 0

Here, Q represents a polynomial.

For instance, a + 6 = 0 is an algebraic equation, here (a+6) represents a polynomial. It is sometimes known as a polynomial equation for this reason.

Make sure that every change on one side of the equation is reflected on the other side to prevent making a mistake that throws the equation out of balance. For instance, you must add the identical number, 6, to the other side of the equation if you want to add 6 to one side of it. The same holds true for division, multiplication, and subtraction. Equations in algebra with only one variable are referred to as univariate equations, while equations with several variables are referred to as multivariate equations.

What Is An Equation?

An equation is a mathematical expression that explains the connection between two values. The two values are normally equated with an equal sign in an equation. For instance, 3x + 6 = 18.

In this equation, x is the only variable. 3x,6, and 18 are the terms. 6 and 18 are the constants. ‘+’ is the operator.

Types Of Algebraic Equations

There are various kinds of algebraic equations. Several of the algebraic equations are:

Polynomial Equations - A polynomial equation is one with variables, exponents, and coefficients.
Quadratic Equations - A polynomial equation with degree 2 and only one variable is referred to as a quadratic equation. It has the form, $f(x)=ax^{2}+bx+c$

Here, the value of a is non-zero.

Cubic Equations - The degree three polynomials are cubic polynomials. Algebraic equations also exist for every cubic polynomial. They are of the form: $ax^{3}+bx^{2}+cx+d=0$
Rational Polynomial Equations - These are equations of the form, $\frac{P(x)}{Q(x)} = 0$.
Trigonometric Equations - A trigonometric equation is one that contains the trigonometric functions of a variable. For instance, $\sin2x=1+6\cos x$

What Is An Algebraic Expression?

An algebraic expression is a polynomial that consists of variables, coefficients, and constants connected by operations like addition, subtraction, multiplication, division, and non-negative exponentiation. It is important to distinguish between an algebraic expression and an algebraic equation. An algebraic equation is created when two algebraic expressions are combined using the "equal to" sign.

Formulas For Algebraic Equations

Numerous formulas and identities can be used to simplify algebraic equations. These speed up the process of solving a particular equation. Some significant algebraic formulas are shown below:

$(a+b)^{2}=a^{2}+2ab+b^{2}$
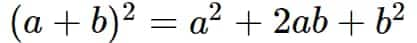
$(a-b)^{2}=a^{2}-2ab+b^{2}$
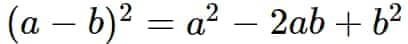
$(a+b)(a-b)=a^{2}-b^{2}$
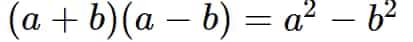
$(x+a)(x+b)=x^{2}+(a+b)x+ab$
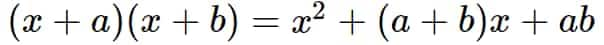
$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
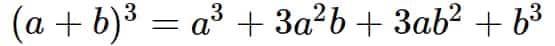
$(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}$
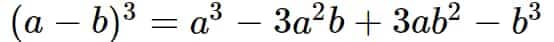
$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$
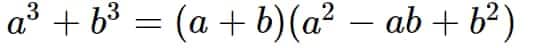
$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$
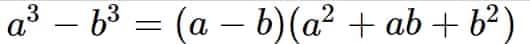
$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2bc+2ca$

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

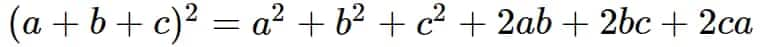
How Are Algebraic Equations Solved?

Depending on the degree, a variety of methods are available to solve algebraic equations. In order to solve an algebraic equation with two variables, two equations must be used. As a result, it can be claimed that the number of variables contained in an algebraic equation will determine how many equations are needed to solve it.

Points To Remember

An algebraic equation is one that is created by combining two algebraic expressions with an equal sign.
Equations involving algebra can be one-, two-, or multiple-step equations.
Based on the degree, algebraic equations are categorized as linear, quadratic, cubic, and higher-order equations.

Frequently Asked Questions (FAQs)

1. What is an algebraic equation?

A mathematical statement in which two expressions are made equal to one another is known as an algebraic equation. Because polynomials are included on both sides of the equal sign, algebraic equations are also referred to as polynomial equations.

2. What is an algebraic equation?

An algebraic equation is a mathematical statement that shows two expressions are equal, usually involving variables represented by letters. It's a way to describe relationships between quantities using mathematical symbols.

3. Name the components of an algebraic equation.

A variable, coefficients, and constants are the typical components of an algebraic equation.

4. Define univariate and multivariate equations.

Equations in algebra with only one variable are referred to as univariate equations, while equations with several variables are referred to as multivariate equations.

5. Name the types of algebraic equations.

There are various kinds of algebraic equations. Several of the algebraic equations are:

Polynomial Equations
Quadratic Equations
Cubic Equations
Rational Polynomial Equations
Trigonometric Equations

6. Define an algebraic expression.

7. What is the standard form of a linear equation?

The standard form of a linear equation is Ax + By = C, where A, B, and C are constants, and x and y are variables. A and B are not both zero.

8. What is the relationship between the roots and coefficients of a polynomial equation?

Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots. For example, in a quadratic ax² + bx + c = 0, the sum of roots is -b/a, and their product is c/a.

9. How do you solve a cubic equation?

Cubic equations (ax³ + bx² + cx + d = 0) can be solved by factoring, using the cubic formula, or graphical methods. Sometimes, they can be solved by grouping or substitution.

10. How do you solve an absolute value equation?

To solve an absolute value equation like |x| = a, consider two cases: x = a and x = -a. For more complex equations, split into cases and solve each separately.

11. What is a radical equation?

A radical equation contains a square root or other root of a variable expression. Solving often involves isolating the radical and then squaring or raising both sides to the appropriate power.

12. What does it mean to "solve" an algebraic equation?

Solving an algebraic equation means finding the value(s) of the variable(s) that make the equation true. It's like finding the "key" that unlocks the equation and makes both sides equal.

13. How do you solve a system of linear equations?

Systems of linear equations can be solved using methods like substitution, elimination, or graphing. The goal is to find values for the variables that satisfy all equations simultaneously.

14. What is the quadratic formula, and when is it used?

The quadratic formula is x = [-b ± √(b² - 4ac)] / 2a, used to solve quadratic equations of the form ax² + bx + c = 0. It's particularly useful when the equation can't be easily factored.

15. What are the roots of a quadratic equation?

The roots of a quadratic equation are the values of x that make the equation true. They are the x-intercepts of the parabola and can be found using the quadratic formula or factoring.

16. How does the discriminant relate to the roots of a quadratic equation?

The discriminant, b² - 4ac, determines the nature of the roots. If it's positive, there are two real roots; if zero, one real root; if negative, two complex roots.

17. How do extraneous solutions arise when solving equations?

Extraneous solutions can occur when we perform operations that may introduce or eliminate solutions, like squaring both sides or multiplying by a variable expression. Always check solutions in the original equation.

18. What is the difference between consistent and inconsistent equations?

Consistent equations have at least one solution, while inconsistent equations have no solution. In a system of equations, consistent equations have at least one point of intersection.

19. What is the difference between an equation and an expression?

An equation contains an equal sign (=) and states that two expressions are equal. An expression is a combination of numbers, variables, and operations without an equal sign.

20. How do you determine if an equation is true for all values of the variable?

An equation true for all values of the variable is an identity. To check, simplify both sides of the equation. If they're identical for all values, it's an identity.

21. How do you factor a polynomial equation?

Factoring involves breaking down a polynomial into simpler terms. Common methods include finding common factors, grouping, and using special formulas like the difference of squares or perfect square trinomials.

22. What are the main types of algebraic equations?

The main types of algebraic equations include linear equations (first degree), quadratic equations (second degree), cubic equations (third degree), and higher-degree polynomial equations. Each type is classified based on the highest power of the variable in the equation.

23. What is a quadratic equation?

A quadratic equation is a second-degree polynomial equation of the form ax² + bx + c = 0, where a ≠ 0, and a, b, and c are constants. Its graph forms a parabola.

24. How do you determine if an algebraic equation is linear?

A linear equation is one where the variable(s) appear only to the first power (no squares, cubes, etc.), and there are no products of variables. If you graph it, it forms a straight line.

25. What is a polynomial equation?

A polynomial equation is an equation where a polynomial is set equal to another polynomial or a constant. The highest degree of the polynomial determines the equation's degree.

26. What is a rational equation?

A rational equation is an equation that contains fractions with variables in the denominators. Solving often involves finding a common denominator and cross-multiplying.

27. How do algebraic equations differ from arithmetic equations?

Algebraic equations contain variables (usually letters) representing unknown values, while arithmetic equations only involve specific numbers. Algebraic equations allow us to solve for unknown quantities and express general relationships.

28. How do algebraic equations relate to functions?

Many algebraic equations can be rewritten as functions. For example, y = 2x + 3 defines a linear function. The solutions to an equation often correspond to the roots or zeros of the related function.

29. What is the connection between algebraic equations and geometry?

Many geometric problems can be expressed and solved using algebraic equations. For example, the equation of a circle (x² + y² = r²) relates algebraic variables to geometric concepts of distance and radius.

30. How do you determine if an equation represents a function?

An equation represents a function if each input (x-value) corresponds to exactly one output (y-value). The vertical line test can be used graphically: if any vertical line intersects the graph more than once, it's not a function.

31. What is the importance of domain and range in algebraic equations?

The domain is the set of possible input values, and the range is the set of possible output values. They're crucial for understanding the behavior and limitations of equations, especially when graphing or finding solutions.

32. What role do parameters play in algebraic equations?

Parameters are constants whose values are not specified in the equation. They allow for the representation of families of equations or solutions. For example, y = mx + b represents all linear equations, with m and b as parameters.

33. What is the significance of the degree of an equation?

The degree of an equation (highest power of the variable) determines the maximum number of solutions. A linear equation (degree 1) has at most one solution, a quadratic (degree 2) at most two, and so on.

34. How do you solve a logarithmic equation?

To solve logarithmic equations, use the properties of logarithms to simplify, then convert to exponential form. For example, log₂(x) = 3 becomes 2³ = x, so x = 8.

35. What is a piecewise-defined equation?

A piecewise-defined equation uses different formulas for different parts of its domain. For example, f(x) = {x² if x ≥ 0; -x if x < 0} is defined differently for positive and negative x values.

36. What is the difference between an equation and an inequality?

An equation states that two expressions are equal, while an inequality compares two expressions using symbols like <, >, ≤, or ≥. Inequalities often have a range of solutions rather than specific values.

37. How do you determine if an equation is symmetric?

An equation is symmetric if it remains unchanged when x and y are interchanged. For example, x² + y² = 1 is symmetric, while y = x² is not.

38. What is a parametric equation?

Parametric equations express the coordinates of a point as functions of a parameter, usually t. For example, x = cos(t) and y = sin(t) parametrically define a circle.

39. How do you determine if an equation is homogeneous?

A homogeneous equation remains valid when all variables are multiplied by the same constant. For example, ax + by = 0 is homogeneous, while ax + by = c (where c ≠ 0) is not.

40. What is a Diophantine equation?

A Diophantine equation is a polynomial equation for which only integer solutions are sought. For example, finding integer solutions to ax + by = c is a Diophantine problem.

41. How do you approach solving trigonometric equations?

Solving trigonometric equations often involves using trigonometric identities, restricting the domain to find principal solutions, and then extending to find general solutions that repeat over the function's period.

42. How do you solve a system of non-linear equations?

Systems of non-linear equations can be solved using substitution, elimination, or graphical methods. Sometimes, algebraic manipulation can transform them into simpler forms.

43. What is the role of the zero product property in solving equations?

The zero product property states that if the product of factors is zero, at least one factor must be zero. This is crucial for solving equations by factoring, as it allows us to set each factor to zero and solve.

44. How do you solve a reciprocal equation?

A reciprocal equation is one where the variable appears in the denominator. To solve, multiply both sides by the common denominator to clear fractions, then solve the resulting polynomial equation.

45. What is the difference between exact and approximate solutions?

Exact solutions are precise mathematical expressions (like √2 or π), while approximate solutions are decimal approximations (like 1.414 or 3.14159). Some equations only have approximate solutions.

46. What is a transcendental equation?

A transcendental equation involves transcendental functions like exponential, logarithmic, or trigonometric functions. For example, sin(x) = x is a transcendental equation.

47. How do you solve equations involving exponential functions?

Equations with exponential functions often require logarithms to solve. For example, to solve 2ˣ = 8, take the log of both sides: log₂(2ˣ) = log₂(8), which simplifies to x = 3.

48. How do you approach solving an equation with multiple variables?

With multiple variables, you typically need as many independent equations as variables to solve the system. Alternatively, you might express one variable in terms of others or use parametric methods.

49. What is the difference between real and complex solutions?

Real solutions are numbers on the real number line, while complex solutions involve the imaginary unit i (√-1). Some equations, like x² + 1 = 0, only have complex solutions.

50. How do you determine if an equation is separable?

A separable equation is one where variables can be completely separated onto different sides of the equation. This is often useful in solving differential equations, where you can integrate both sides separately.

51. How do you determine if an equation is continuous?

An equation represents a continuous function if there are no breaks or jumps in its graph. Algebraically, this often involves checking for undefined points (like division by zero) and ensuring the left and right limits match at all points.

52. How do implicit and explicit equations differ?

An explicit equation directly expresses one variable in terms of others (like y = 2x + 3), while an implicit equation relates variables without isolating one (like x² + y² = 1).

53. What is the significance of the Fundamental Theorem of Algebra?

The Fundamental Theorem of Algebra states that every non-constant polynomial equation with complex coefficients has at least one complex solution. This guarantees that an nth-degree polynomial has exactly n complex roots (counting multiplicity).

54. How do you determine if an equation is invertible?

An equation represents an invertible function if each y-value corresponds to a unique x-value. Graphically, this is tested using the horizontal line test. Algebraically, you check if you can solve for x uniquely in terms of y.

55. What is the relationship between algebraic equations and mathematical modeling?

Algebraic equations are fundamental tools in mathematical modeling, allowing us to represent real-world relationships and phenomena in mathematical terms. They enable prediction, analysis, and optimization in various fields like physics, economics, and engineering.