Fundamental Geometry Concepts for 2D Shapes: Definitions, Properties, and Examples

Comprehending fundamental geometric ideas is essential for candidates getting ready for design aptitude exams such as NID and UCEED. The Understanding of basic geometric concepts is vital for NAT(Numerical Aptitude Test) in various DAT examinations conducted by most reputed D-Schools. To maximize your chances of acing the test, you must understand the fundamentals of dimensions. This will boost your technical expertise as well as your creative capacity to come up with workable design solutions.

Introduction to Basic Geometric Shapes

1. CIRCLE:

A circle is a round shape where every point along its edge is equidistant from a central point.

Examples: Common examples of circles include coins, wheels, and clocks.

Formula: Area = π × R², where R is the radius.

Major Sector: A circle division with a centre angle larger than 180 degrees.

Minor Sector: A division of the circle distinguished by Less than 180° is the central angle that characterises it.

Let’s understand this with an example of pizza and a slice. Consider the pizza as a full circle, and the slice can be considered a minor sector.

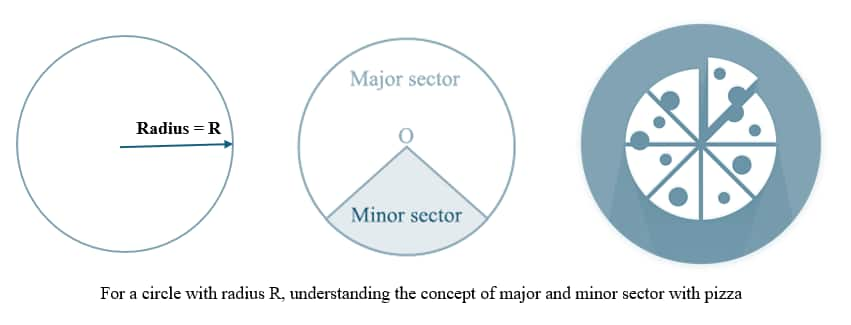
Example: Understanding through an example of a Pizza cut

Calculating the Area of a Sector : (θ/360°) × πr2

Where θ = angle of the sector

r = Radius of circle

2. PARALLELOGRAM:

It is a four-sided polygon with parallel and equal opposite sides.

Properties of a Parallelogram

Understanding the properties of the parallelogram is required for the practical application as asked in diverse Numerical Aptitude and Design Aptitude Sections of the different examinations.

For the above parallelogram, consider the following properties:

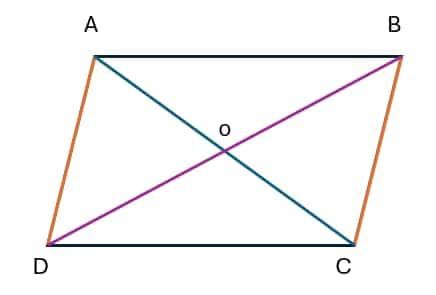
1. The opposing sides are parallel.

In this case, AB || DC & AD || BC

2. In a parallelogram, the opposing sides are always equal.

In this case, AB=DC and AD=BC

3. For a parallelogram, the opposite angles are equal.

In this case, ∠A= ∠C and ∠B=∠D

4. A parallelogram's diagonals cut each other in half.

In this case, AO = OC and BO = OD

5. Interior angles on the same side complement one another.

In this case, ∠ADC + ∠DCB = 180∘, Similarly ∠DCB + ∠CBA = 180∘,

∠CBA + ∠ABD = 180∘, ∠BAD + ∠ADC = 180∘.

6. The parallelogram is divided into two congruent triangles by the diagonals.

Here, ΔADB and ΔDCS are congruent, while ΔADC and ΔABC are congruent.

Classification of Parallelogram: It can be classified mainly into three distinct types as follows :

2a. Square

2b. Rectangle

2c. Rhombus

2a. Square :

Examine the ABCD square and associate it with the subsequent attributes.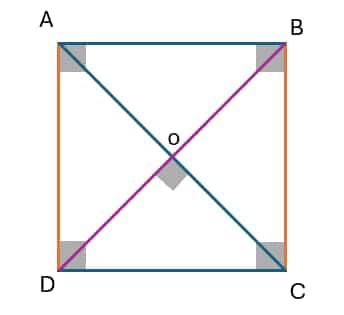

A square possesses the following properties:

1. Four equal sides. In this case, AB = BC = CD = DA

2. Four angles to the right. Here, ∠A = ∠B = ∠C = ∠D =90∘

3. Two sets of sides that are parallel to one another. In this case, AB || DC, AD || BC

4. A pair of diagonals that are equal. In this case, AC = BD.

5. Diagonals are perpendicular to one another. In this case, AC⊥BD

6. Diagonals bisect each other in half

Area of the Square = Side(AB) X Side(BC)

Perimeter of the Square = 4 X Side

2b. Rectangle

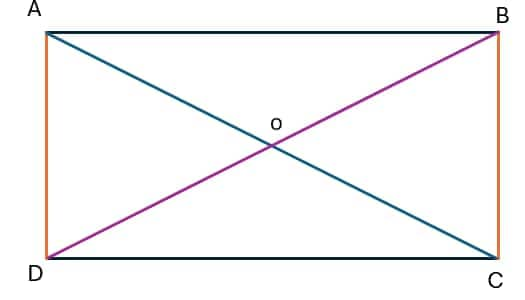
Examine the ABCD rectangle and associate it with the following characteristics. A rectangle possesses:

1. Two sets of sides that are parallel to one another. In this case, AB || DC, AD || BC

2. All Four angles are right angles. Here, ∠A = ∠B = ∠C = ∠D = 90∘

3. Opposite sides are equal in length. This time, AD = BC and AB = DC.

4. A pair of diagonals that are equal. In this case, AC = BD.

5. Diagonals that split others into half.

Area of the Rectangle = Length (DC) X Breath (AD)

The perimeter of the Rectangle = 2 (Length + Breadth)

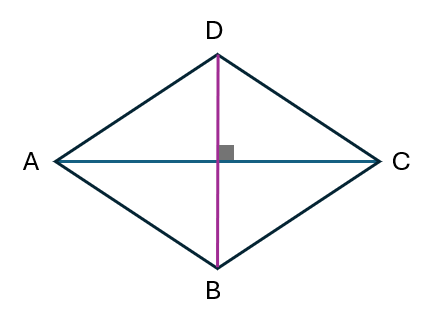
2c. Rhombus

Examine the rhombus EFGH to associate it with the subsequent characteristics. A Rhombus possesses:

1. Two sets of sides that are parallel to one another. In this case, AB || DC and BC || AD

2. Four equal sides. Here, AB=BC=CD=DA

3. Opposite angles are equal, H = F and ∠E = ∠G

4. Diagonals run parallel to one another. In this case, AC⊥BD

5. Diagonals(AC & DB) split each other into two halves.

Area of the Rhombus = (Diagonal 1 X Diagonal 2) / 2

Perimeter of the Square = 4 X Side

3. TRIANGLES

A triangle, one of the fundamental geometric shapes, is a polygon with three corners and three sides. The sides joining the corners, also known as edges, are one-dimensional line segments, whereas the corners, also known as vertices, are zero-dimensional points.

Classification of Triangles Based on Sides

3a. Isosceles Triangles

3b. Scalene Triangle

3c. Equilateral Triangle

We will cover the fundamentals of the triangles one by one to understand the basics for application:

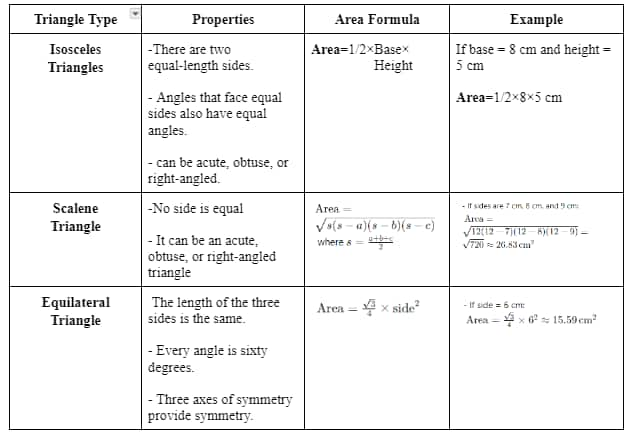
Here in the below table, the properties & Areas of different types of Triangle is covered :

You can also refer to:

• Simple Machines (Part-1): Inclined Plane & Lever
• Visualisation Analogy
• Fundamentals of Geometry for 3D Shapes

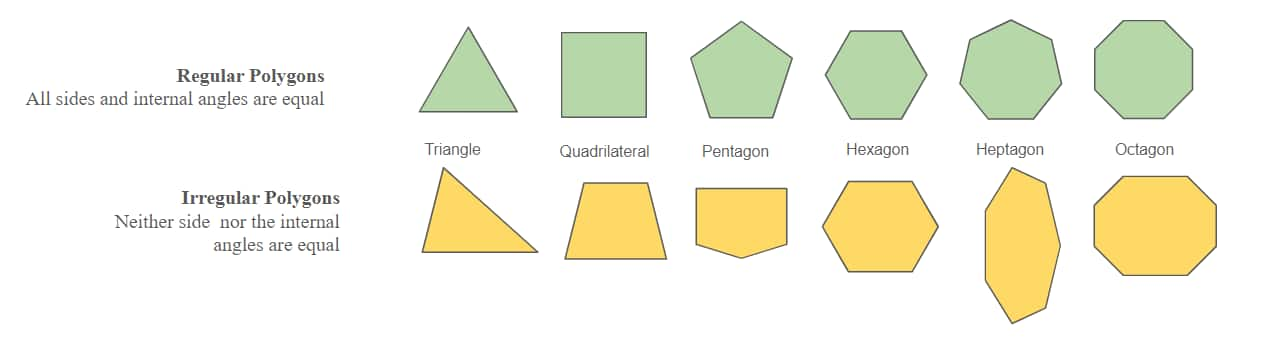
4. POLYGONS

The term “polygon” is derived from the word ‘poly’ meaning ’many’ and ‘gon’ meaning ‘Angle’.

Polygons are defined as two-dimensional closed shapes formed by joining three or more line segments with each other. We encounter polygons mostly while we learn about geometry. In this lesson, we will learn about polygons' definitions, regular polygons, polygon sides, and the properties of polygons, along with polygon examples and their identification.

Properties of a Polygon

1. It is composed of three or more sides.

2. The polygon's angles might or might not be equal.

3. A polygon's sides could all be the same length or different.

4. It is a planar shape, meaning that it is composed of straight lines or line segments.

5. It is a two-dimensional figure, meaning its length and breadth are its only two dimensions. It has no height or depth.

6. A polygon is a closed shape; it does not have any open ends. It starts and finishes at the exact location.

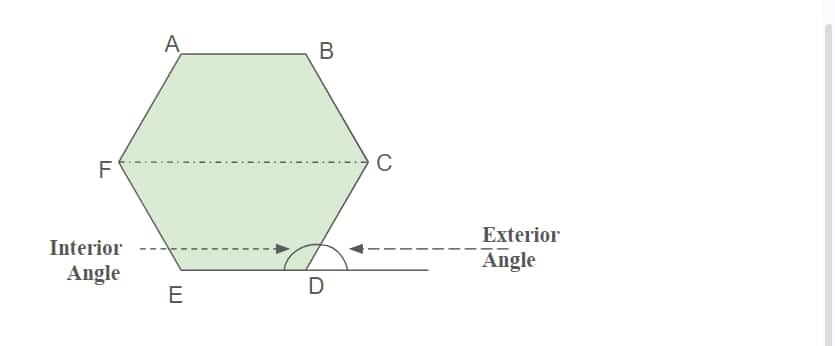
In this case a Regular Hexagon

• The diagonal is FC.

• Every inner angle is equal.

• Every external angle is equal.

• The hexagon's vertices are A, B, C, D, E, and F.

• This regular hexagon has equal sides, which are as follows:

AB = BC = CD = DE = EF = FA.

Types of Polygons

There is a range of polygons based on the number of sides from a minimum of 3 sides(Triangle) to even up to 20 (Icosagon)

Based on the length of its sides and the measurement of its angles, a polygon can be classified as either regular or irregular.

1. Triangle (3 sides)

A triangle is the simplest polygon, consisting of three sides and three angles. The interior angles of a triangle always sum up to 180°. Based on the length of the sides and the measure of the angles, triangles are further classified as:

• Equilateral Triangle: All three sides and angles are equal, with each angle measuring 60°.
  
  

• Isosceles Triangle: Two sides are equal, and the angles opposite those sides are also equal.
  
  

• Scalene Triangle: All sides and angles are different.
  
  

The area of a triangle can be calculated using the formula:

Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21×base×height

2. Quadrilateral (4 sides)

A quadrilateral has four sides and four angles, with the interior angles always summing up to 360°. Some common types of quadrilaterals include:

• Square: All sides are equal, and all angles are 90°.
  
  

• Rectangle: Opposite sides are equal, and all angles are 90°.
  
  

• Rhombus: All sides are equal, but angles are not 90°.
  
  

• Trapezoid: Only one pair of opposite sides is parallel.
  
  

• Parallelogram: Opposite sides are parallel and equal in length.
  
  

The area of a general quadrilateral can be calculated using:

Area=base×height\text{Area} = \text{base} \times \text{height}Area=base×height

3. Pentagon (5 sides)

A pentagon has five sides and five angles. In a regular pentagon, all sides and angles are equal. The interior angles of a regular pentagon each measure 108°, and the sum of the interior angles is 540°.

The area of a regular pentagon can be calculated using the formula:

Area=14×5(5+25)×side2\text{Area} = \frac{1}{4} \times \sqrt{5(5 + 2\sqrt{5})} \times \text{side}^2Area=41×5(5+25)×side2

Regular pentagons are seen in architecture, design, and nature (e.g., star shapes).

4. Hexagon (6 sides)

A hexagon has six sides and six angles. In a regular hexagon, all sides are equal, and each interior angle measures 120°. The hexagon is a common shape in nature, particularly in honeycombs, where the hexagonal shape allows for optimal use of space.

The area of a regular hexagon can be calculated as:

Area=332×side2\text{Area} = \frac{3\sqrt{3}}{2} \times \text{side}^2Area=233×side2

Hexagons are often used in tiling and pattern design because they fit together perfectly without gaps.

5. Heptagon (7 sides)

A heptagon has seven sides and seven angles. The interior angles of a regular heptagon each measure approximately 128.57°, and the sum of the interior angles is 900°.

Heptagons are less common in everyday life but can be seen in certain architectural designs and in some art forms.

6. Octagon (8 sides)

An octagon has eight sides and eight angles. In a regular octagon, each interior angle measures 135°, and the sum of the interior angles is 1080°.

A regular octagon is commonly seen in stop signs and in various design patterns. The area of a regular octagon can be calculated using:

Area=2(1+2)×side2\text{Area} = 2(1 + \sqrt{2}) \times \text{side}^2Area=2(1+2)×side2

7. Nonagon (9 sides)

A nonagon has nine sides and nine angles. The interior angles of a regular nonagon each measure 140°, and the sum of the interior angles is 1260°. Nonagons are less commonly seen but can appear in certain architectural designs.

8. Decagon (10 sides)

A decagon has ten sides and ten angles. In a regular decagon, each interior angle measures 144°, and the sum of the interior angles is 1440°.

Decagons are used in various fields of geometry and design.

9. Icosagon (20 sides)

An icosagon is a polygon with twenty sides and twenty angles. The interior angles of a regular icosagon each measure 162°, and the sum of the interior angles is 3240°.

Icosagons are often seen in complex geometrical designs or used in certain types of high-level mathematics or theoretical geometry.

Perimeter of a Polygon

A polygon's perimeter is its entire boundary measured from end to end. Since polygons are closed-plane shapes, their perimeters fall inside two-dimensional planes.

Q: Calculate the Perimeter of a Regular Pentagon for a side light of 5 cm.

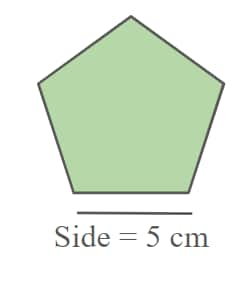
A: Since it’s a regular pentagon, all the sides are equal

Perimeter = Sum of All sides

Perimeter = 5 X (5)

Area of a Polygon

The area of a Polygon is the region or space occupied inside a polygon.

A polygon can be classified as regular or irregular, depending on how long its sides are. Therefore, there is a discrepancy in the area of polygons calculated due to this differentiation. The following are some well-known polygons' areas:

Note: The questions asked in the Design aptitude examination may not ask you to calculate the area of a given figure directly, but mostly the questions asked are application-based.

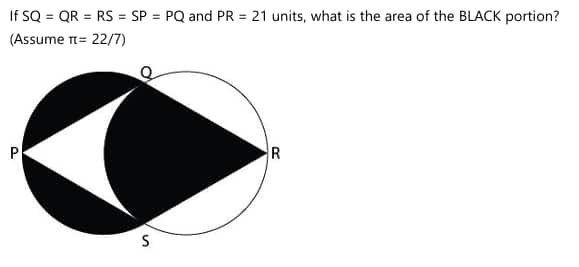
Sample Question From Previous Year Exams: UCEED/NID- DAT