Accuracy Precision Measurement

Accuracy Precision Measurement - A Complete Guide

Edited By Team Careers360 | Updated on Jul 02, 2025 05:00 PM IST

We will discuss precision meaning, accurate meaning, Accuracy and precision definition, precise meaning, and accurate meaning, accuracy, and precise meaning
Precise meaning:-. What is the meaning of precise? To be precise meaning a specific value that may or may not be accurate.
Accurate meaning:- We can define accurately as exact value or near the true value.

Accuracy Precision Measurement - A Complete Guide

What is accuracy and precision, let’s discuss in detail.

Accuracy and precision:-What is accuracy? and what is precision? In common language the phrase accuracy and precision convey almost the same meaning but in science the same is not true; a measurement may give precise measurement but it can be quite inaccurate at the same time. So, what is accuracy in physics and what is precision in physics? And also what is accuracy and precision in chemistry. To understand the distance between terms, let’s take an example in which a person doing shooting practice and is allowed to shoot six bullets and aiming at Bull’s eye in a target frame consisting of circular regions of varying radius.

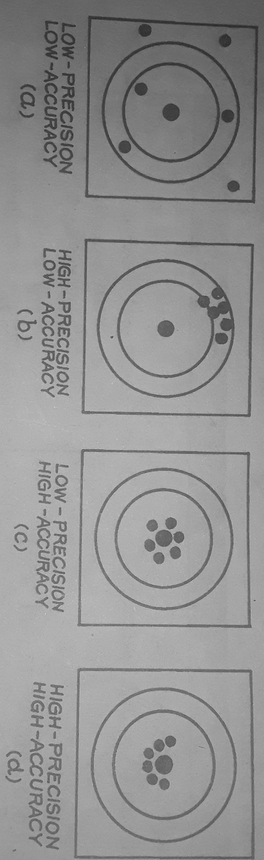
Accuracy and precision

Center is bull’s eye
Bullet shots.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

In fig a, the shots hit the target frame in the outer circle and are scattered widely with respect to each other. Hence, it is a case of low precision and low accuracy. In fig b, the bullets are marked in the outer circular region away from target but are clustered in a very small region. Thus it is a case of low accuracy and high precision. Further in fig c, although the bullet spots are scattered widely with respect to each other, yet these spots are in an internal circular region, very close to the Bull’s eye therefore,it is a case of low precision and high accuracy. And finally in figure d the spots are clustered with respect to each other and simultaneously these are very close to the Bull’s eye. Therefore it is a case of high precision and high accuracy.

So, now we understand what is meant by the term accuracy and what is meant by precision. So, we can define accuracy and precision as

Accuracy is defined as, ‘’ the extent up to which an observe value agrees with the true value of a quantity (or closeness of measured value to true value is) is known as it’s accuracy’’

And the instrument which gives repeated readings close to the true value of the physical quantity under consideration, is an accurate instrument. On the other hand, we can define precise as the precision of an observed value tells what resolution the quantity is measured. Thus, the measured values which are very close to each other (may or may not be close to the true value) are precise values and an instrument which gives a tight cluster of repeated results is a precise instrument.

Precise meaning in tamil is துல்லியமான. Accuracy meaning in tamil is திட்பநுட்பம். Accuracy meaning in gujarati is ચોકસાઈ

Also read -

Accuracy vs Precision:- We can distinguish accuracy and precision as

“ the precision of an observed value tells what resolution the quantity is measured”.

“The extent up to which an observed value agrees with the true value of a quantity is known as its accuracy.”

The accuracy of the measurement is determined by absolute error. The accuracy depends upon significant figures .Measurement which is close to true value is known as accuracy.

Accuracy Precision of an instrument and errors in measurement:-

Accuracy and Precision in measurement:- The accuracy of an instrument

depends more on systematic error (for example calibration error, zero error, etc,.) present in it rather than some other factors. It can be improved by applying a proper correction. Higher the accuracy , smaller the error.

Thus, an error gives the indication of accuracy. On the other hand, precision depends on random errors. precision of an instrument is defined as degree of freedom from random errors Therefore, it can be eradicated. Moreover, higher is the precision, larger is the number of significant figures. Thus, the precision gives the indication of the number of significant figures in a measurement. Precision of measurement depends on the least count of the instruments. Some precision measurement instruments are screw gauge, vernier callipers, and dial indicator etc.

Error in the measurement:- In the measurement taken during an experiment in the laboratory, two types of errors are present; errors of observation and error present in the instrument. Uncertainty of measurement is technically called an error. Error is always expressed in percentage.

Mainly, errors are two types:

(i) Systematic errors:- These errors occur constantly in an experiment repeated under identical conditions.These errors come into existence by virtue of a definite rule.Therefore, once the rule which governs these errors is identified these errors can be eradicated by applying proper corrections to the result obtained.

(ii) Random errors:-These arise due to (i) small changes in the condition of the experiment and (ii) incorrect judgement of the observer in taking readings.

Methods of minimising random errors:- The random error can be minimised by taking the arithmetic mean of a large number of readings of the same quantity.

NCERT Physics Notes :

Absolute error:- The magnitude of the difference between the true value (or value obtained after taking arithmetic mean) of the measured quantity and the individual measured value is called an absolute error.

∴ An absolute error = True value ~ measured value

Let a1, a2, a3, ….an are the measured values of the physical quantity, the absolute error.

?a1 = ¯a ~ a1

?a2 = ¯a ~ a2

…………………………...

?an = ¯a ~ an

Where ¯a is a mean value or true value.

Mean absolute Error:- The arithmetic mean of the absolute error of the different measurement is called mean absolute error.

Mean absolute error, ¯?a = 丨?a1丨+ 丨?a2丨+ 丨?a3丨/ n

¯?a = 1/n ∑ 丨?ai丨

Related Topics Link,

Accuracy and precision examples:-

accuracy and precision examples

A screw gauge is a precise instrument because it gives precise measurement of the diameter of the wire but a thermometer is an accurate instrument because it gives an accurate measurement of temperature. So, the accuracy example is the thermometer and the precision example is screw gauge.

which of the following measurement is most precise
6.00 mm
6.00 cm
6.00 m
60.00 m

Correct option is 6.00 mm

which of the following instruments is most accurate
0.006 mm
6.00 mm
60.00 mm
6.0 mm

Correct option is 0.006 mm

What is meant by measurement or what is the definition of the measurement:-Measurement can be defined as numbers linked to the physical quantity which can be measured size, capacity, time, etc,. Concept of measurement is important in our daily life.

Need of measurement:- But what is the need of measurement? Lord Kelvin once said, “ when you can measure what you are speaking about and express it in numbers, you know about it; but when you cannot express it in numbers, your knowledge is of meagre and unsatisfactory kind. For example, if you want to buy milk but you don’t know how much? Because you don't know the quantity of milk. If you want to tell someone how much time you studied or played then how can you tell them if you do not know that in which quantity time can be measured but if you know that you can easily tell them i studied or played for one hour. So, we measure length in meters or kilometers, weight in kg, velocity in speed/second, etc,. These are the examples of measurement.

Also Read :

How to calculate the accuracy and precision:-

The reliability of two voltmeters A and B of range 3V each, is examined against a standard voltage source of emf 1.018 V . The voltage of source is measured five times and the corresponding reading of voltmeters in all five sets are recorded as under in a tabular form :

Reading of Voltmeter A (volt)	Reading of Voltmeter B (volt)
1.01	2.02
1.07	2.04
1.06	2.03
1.09	2.05
1.08	2.01

Which voltmeter gives precise measurement and which has higher accuracy? Explain.
What may be the actual cause due to which reading of voltmeter B is greater than2 V in all five sets though emf of source is 1.018 only?

Solution. (1) The variation in the reading shown by voltmeter A = 1.09 - 1.01 = 0.08 V

And the variation in the reading of voltmeter B =2.05 - 2.01 = 0.04 V

Since the variations in the readings shown by voltmeter B are smaller compared to that of voltmeter A, which means the values recorded by voltmeter B are very close to each other, hence voltmeter B has greater precision.

Now, the arithmetic mean of readings shown by voltmeter A = 1.01 + 1.07 + 1.09 + 1.08 / 5V = 1.06 V

And the arithmetic mean of the readings of voltmeter B = 2.02 + 2.04 + 2.03 + 2.05 + 2.01 / 5 V = 2.03 V

Since, the average reading of voltmeter A is close to the true value (1.018 V) therefore, voltmeter A is more accurate.

(2) Since, the source voltage is 1.018 V, therefore any correct voltmeter cannot record the potential difference of the force greater than this value. However, it is possible only when there is some error in the meter. Prima Facie it seems that voltmeter B has a zero error of 1 V. If this error is eradicated by applying proper corrections, it would give an accurate as well as precise readings.

2. In an experiment of a simple pendulum, a student made several observations for the period of oscillation. His readings turned out to be 2.63 s, 2.56 s, 2.42 s, 2.71 s and 2.80 s. Find (i) mean period of oscillation, or most accurate valueof time period. (ii) absolute error in each reading, (iii) mean absolute error, (iv) fractional error and (v) percentage error.

Solution. (i) The mean period of oscillation of the pendulum is

T = 2.63 + 2.56 + 2.42 + 2.71 + 2.80 / 5 s =

13.12 / 5 s = 2.624 s = 2.62 s. (rounded off to second decimal place)

(ii) Taking 2.62 s as the true value, the absolute errors ( true value - measured value ) in the five readings taken are :

2.62 s - 2.63 s = - 0.01 s, 2.62 s - 2.56 s = 0.06 s, 2.62 s - 2.42 s = 0.20 s, 2.62 - 2.71 s = - 0.09 s, 2.62 s - 2.80 s = - 0.18 s.

(iii) The (maximum) mean absolute error is

(?T) max = 0.01 + 0.06 + 0.20 + 0.09 + 0.18 / 5 sec

= 0.54 / 5 s = 0.108 s = 0.11 s. (rounded off to second decimal place)

(iv) The maximum fractional error is

(?T/T)max = 0.11 s/ 2.62 s = 0.0419 = 0.04.

(v) The percentage error is

(?T/T) max multiply 100 = 0.04 x 100 = 4%

The value of T should be written as

T =(2.62 +- 0.11) s.

As the arithmetic mean of all the absolute errors is 0.11 s, there is already an error in the first decimal place. Hence, there is no point in giving the period up to second decimal place . We should, more correctly, write

T = (2.6 +- 0.1) s.

Also check-

Frequently Asked Questions (FAQs)

1. What do you mean by accuracy?

Accuracy definition physics:- To extent up to which an observed value agrees with the true value of a quantity is known as accuracy.

2. Define precision in physics, what is precision in chemistry?

Precision in physics and chemistry is almost the same.

Precision is defined as, precision of an observed value tells to what resolution the quantity is measured.

3. Difference between measured value and true value.

An absolute error is the difference between true value and measured value

Absolute error = True value - measured value

4. Name the measuring instruments in physics.

Some of the instruments are screw gauge, vernier calipers, speedometer, ammeter, voltmeter, compass etc,.

5. Define measurement.

Measurement can be defined as numbers linked to the physical quantity which can be measured size, capacity, time, etc,.

6. What's the difference between accuracy and precision in measurements?

Accuracy refers to how close a measurement is to the true value, while precision refers to how consistent or reproducible measurements are. An accurate measurement is close to the actual value, whereas precise measurements are close to each other but not necessarily to the true value.

7. Can a measurement be precise but not accurate?

Yes, a measurement can be precise but not accurate. This occurs when repeated measurements are consistent with each other (high precision) but are systematically off from the true value (low accuracy). For example, if a scale consistently measures 1 kg too high, it's precise but not accurate.

8. How does systematic error affect accuracy and precision?

Systematic errors affect accuracy but not precision. They cause measurements to be consistently off in one direction, making them inaccurate. However, the measurements may still be precise if they're consistently off by the same amount.

9. What's the relationship between significant figures and precision?

Significant figures indicate the precision of a measurement. More significant figures suggest higher precision, as they show that the measurement was made with a more sensitive instrument or technique.

10. How do random errors impact measurements?

Random errors affect precision but not necessarily accuracy. They cause measurements to fluctuate unpredictably around the true value, reducing consistency (precision) but not systematically shifting the average away from the true value.

11. What's the importance of uncertainty in measurements?

Uncertainty quantifies the doubt about the validity of a measurement result. It's crucial because it provides information about the reliability and limitations of the measurement, allowing for meaningful comparisons and conclusions.

12. How does the choice of measuring instrument affect accuracy and precision?

The choice of measuring instrument impacts both accuracy and precision. More sensitive instruments generally provide higher precision, while well-calibrated instruments offer better accuracy. The instrument's resolution also limits the precision of measurements.

13. What's the difference between absolute and relative error?

Absolute error is the difference between the measured value and the true value, expressed in the same units as the measurement. Relative error is the absolute error divided by the true value, often expressed as a percentage, providing a scale-independent measure of error.

14. How does repeating measurements improve results?

Repeating measurements helps reduce the impact of random errors by allowing for the calculation of an average value. This average is likely to be closer to the true value than any single measurement, improving overall accuracy and precision.

15. What's the significance of error propagation in complex measurements?

Error propagation is important in complex measurements involving multiple variables because uncertainties in individual measurements combine to affect the final result. Understanding error propagation helps in estimating the overall uncertainty of the final calculated value.

16. How do calibration and standardization improve measurement accuracy?

Calibration and standardization improve accuracy by comparing measurements to known standards. This process helps identify and correct systematic errors, ensuring that the measuring instrument provides results closer to the true values.

17. What's the role of significant figures in reporting measurements?

Significant figures communicate the precision of a measurement. They indicate which digits are reliably known and which are uncertain. Using the correct number of significant figures prevents overstating the precision of a measurement.

18. How does the concept of tolerance relate to accuracy and precision?

Tolerance is the acceptable range of variation in a measurement. It's related to both accuracy and precision, as it defines the limits within which a measurement is considered acceptable, taking into account both systematic and random errors.

19. What's the importance of traceability in measurements?

Traceability ensures that a measurement can be related to national or international standards through an unbroken chain of comparisons. It's crucial for maintaining consistency and reliability in measurements across different locations and times.

20. How do environmental factors affect measurement accuracy and precision?

Environmental factors like temperature, humidity, and vibrations can affect both accuracy and precision. They can introduce systematic errors (affecting accuracy) or increase random fluctuations (affecting precision) in measurements.

21. What's the difference between accuracy class and accuracy?

Accuracy class is a standardized specification for measuring instruments, indicating the maximum permissible error as a percentage of the full scale. Accuracy, on the other hand, refers to how close a specific measurement is to the true value.

22. How does the concept of resolution relate to precision?

Resolution is the smallest change in a quantity that can be detected by a measuring instrument. It sets a lower limit on the precision of measurements, as you can't measure more precisely than the resolution of your instrument allows.

23. What's the importance of repeatability in measurements?

Repeatability is a measure of precision under constant conditions. It's important because it indicates how consistently an instrument can produce the same result for repeated measurements of the same quantity, which is crucial for reliable scientific observations.

24. How does reproducibility differ from repeatability?

While repeatability refers to the consistency of measurements under constant conditions, reproducibility refers to the consistency of measurements under changed conditions (e.g., different operators, instruments, or locations). Reproducibility is typically lower than repeatability.

25. What's the significance of the least count in measurements?

The least count is the smallest measurement that can be taken accurately with a given instrument. It's significant because it determines the precision limit of the instrument and influences the number of significant figures in the measurement.

26. How do systematic and random errors combine to affect overall measurement uncertainty?

Overall measurement uncertainty is a combination of systematic and random errors. Systematic errors contribute to inaccuracy, while random errors affect precision. The total uncertainty is typically calculated by combining these errors using statistical methods.

27. What's the importance of significant figures in calculations involving measurements?

Significant figures in calculations ensure that the precision of the result reflects the precision of the input measurements. Using too many significant figures can imply a higher precision than is justified by the original measurements.

28. How does the concept of accuracy relate to trueness in measurements?

Trueness is the closeness of agreement between the average of a large number of measurements and the true value. It's closely related to accuracy but specifically refers to the absence of systematic error in the average of many measurements.

29. What's the role of statistical analysis in improving measurement accuracy and precision?

Statistical analysis helps in quantifying and reducing uncertainties in measurements. It allows for the identification of outliers, estimation of random errors, and calculation of confidence intervals, all of which contribute to improving both accuracy and precision.

30. How does the choice of measurement method affect accuracy and precision?

Different measurement methods can have varying levels of accuracy and precision. Some methods may be more prone to systematic errors (affecting accuracy) while others might be more susceptible to random fluctuations (affecting precision). Choosing the appropriate method is crucial for obtaining reliable results.

31. What's the significance of the accuracy-precision trade-off in measurements?

The accuracy-precision trade-off refers to situations where improving one aspect may come at the cost of the other. For example, increasing the sensitivity of an instrument might improve precision but could introduce systematic errors, reducing accuracy.

32. How does rounding affect the reporting of measurements?

Rounding affects the reported precision of measurements. Proper rounding ensures that the reported value reflects the true precision of the measurement, while improper rounding can imply a higher or lower precision than actually achieved.

33. What's the importance of error bars in graphical representations of data?

Error bars visually represent the uncertainty in measurements on graphs. They are crucial for accurately interpreting data, as they show the range within which the true value is likely to lie, helping to assess the significance of trends or differences in data.

34. How does the concept of accuracy relate to bias in measurements?

Bias in measurements is a systematic deviation from the true value, directly affecting accuracy. An unbiased measurement is accurate on average, while a biased measurement consistently deviates from the true value in a particular direction.

35. What's the role of calibration curves in improving measurement accuracy?

Calibration curves relate instrument readings to known standard values, helping to correct for systematic errors and non-linearities in the measurement process. They are essential for improving accuracy, especially in complex or indirect measurements.

36. How does the concept of precision relate to the standard deviation of measurements?

Standard deviation is a statistical measure of precision. It quantifies the spread of measurements around their mean value. A smaller standard deviation indicates higher precision, as the measurements are more tightly clustered.

37. What's the significance of significant figures in expressing uncertainty?

Significant figures in uncertainty expressions indicate the precision of the uncertainty itself. Typically, uncertainties are reported with one or two significant figures to avoid implying more precision in the error estimate than is justified.

38. How does the concept of accuracy relate to the mean of repeated measurements?

The mean of repeated measurements is often used as an estimate of the true value, assuming random errors cancel out. The closeness of this mean to the actual true value is a measure of accuracy, provided systematic errors are minimized.

39. What's the importance of instrument sensitivity in measurements?

Instrument sensitivity determines the smallest change in the measured quantity that can be detected. Higher sensitivity allows for more precise measurements but may also make the instrument more susceptible to noise and environmental fluctuations.

40. How does the concept of precision relate to the reproducibility of measurements?

Reproducibility is an aspect of precision that focuses on the consistency of measurements under varying conditions. High reproducibility indicates good precision even when factors like operators, instruments, or environments change.

41. What's the role of significant figures in comparing measurements?

Significant figures are crucial when comparing measurements as they indicate the precision of each measurement. Comparisons should be made only to the least precise measurement involved, as indicated by the number of significant figures.

42. How does the choice of reference point affect measurement accuracy?

The choice of reference point can significantly impact accuracy. An inappropriate or unstable reference point can introduce systematic errors. A well-defined, stable reference point is essential for accurate measurements, especially in fields like surveying or time measurement.

43. What's the importance of measurement resolution in digital instruments?

Measurement resolution in digital instruments determines the smallest change that can be displayed. It sets a lower limit on precision and can affect accuracy if it's too low. High resolution doesn't guarantee high accuracy but is necessary for precise measurements.

44. How does the concept of accuracy relate to the accuracy rating of an instrument?

An instrument's accuracy rating specifies its expected performance under normal operating conditions. It indicates the maximum deviation from the true value that can be expected, helping users understand the limitations of the instrument's accuracy.

45. What's the significance of the uncertainty principle in quantum measurements?

The uncertainty principle in quantum mechanics sets fundamental limits on the precision with which certain pairs of physical properties can be determined. It demonstrates that there are inherent limitations to measurement accuracy at the quantum level.

46. How does the concept of precision relate to the concept of significant digits?

Significant digits (or figures) are a way of expressing precision in measurements. The number of significant digits indicates how precisely a measurement was made, with more digits suggesting higher precision.

47. What's the role of data validation in ensuring measurement accuracy?

Data validation involves checking the quality and reliability of measured data. It helps identify outliers, systematic errors, and other anomalies that could affect accuracy. Proper data validation is crucial for ensuring the integrity and reliability of measurement results.

48. How does the concept of accuracy relate to the concept of trueness in analytical chemistry?

In analytical chemistry, trueness refers to the closeness of agreement between the average value obtained from a large series of test results and an accepted reference value. It's closely related to accuracy but specifically focuses on the absence of systematic error.

49. What's the importance of measurement range in relation to accuracy and precision?

Measurement range affects both accuracy and precision. Instruments are typically most accurate and precise within their designed range. Operating outside this range can lead to decreased accuracy and precision, or even erroneous readings.

50. How does the concept of precision relate to the repeatability coefficient?

The repeatability coefficient is a statistical measure of precision under repeatability conditions. It represents the value below which the absolute difference between two repeated measurements is expected to lie with a probability of 95%, providing a quantitative measure of precision.

51. What's the significance of the accuracy-to-tolerance ratio in manufacturing?

The accuracy-to-tolerance ratio (A:T ratio) in manufacturing compares the accuracy of a measuring instrument to the tolerance of the part being measured. A lower A:T ratio indicates a more suitable measurement system for the given tolerance, ensuring reliable quality control.

52. How does the concept of accuracy relate to the concept of bias in statistical measurements?

In statistical measurements, bias refers to a systematic error that consistently skews results in a particular direction. It directly affects accuracy, as a biased measurement will consistently deviate from the true value, even if it's precise.

53. What's the role of measurement uncertainty in conformity assessment?

Measurement uncertainty is crucial in conformity assessment as it helps determine whether a measured value truly meets specified requirements. Without considering uncertainty, there's a risk of falsely accepting or rejecting a product based on measurements alone.

54. How does the concept of precision relate to the concept of measurement noise?

Measurement noise refers to random fluctuations that affect the precision of measurements. Higher noise levels result in lower precision, as the random variations make it harder to obtain consistent results in repeated measurements.

55. What's the importance of traceability in maintaining measurement accuracy over time?

Traceability ensures that measurements can be related to national or international standards through an unbroken chain of comparisons. This is crucial for maintaining accuracy over time and across different locations, allowing for reliable comparisons and consistency in scientific and industrial measurements.