Centripetal and Centrifugal Force - Definition, Formula, Example, FAQs
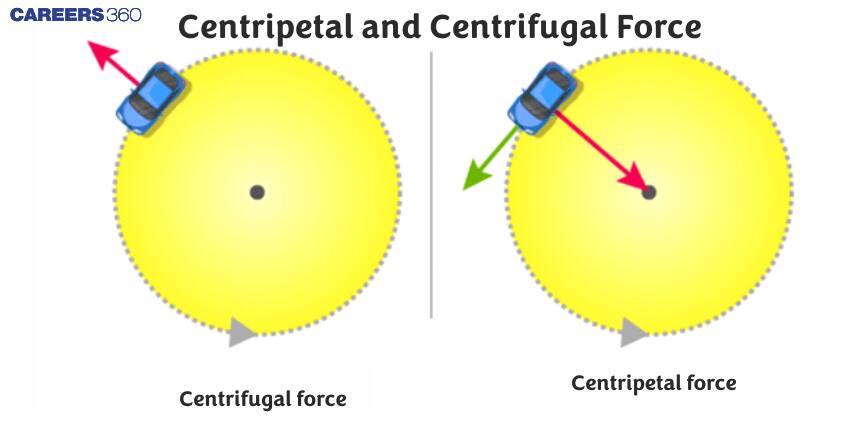
When an object moves in a circle, it does not move straight. Its direction keeps changing again and again. To make this possible, a force is needed. This force is called centripetal force. It always pulls the object towards the centre of the circular path. For example, when you swing a stone tied to a string, the string pulls the stone inward and keeps it moving in a circle. Sometimes we feel another force pushing us outward while turning. This is called centrifugal force. It is not a real force but a feeling seen from a rotating frame. Learning centripetal and centrifugal forces helps us explain circular motion easily and is important for school exams, JEE, and NEET.
This Story also Contains
- What is the Centripetal Force?
- Calculating Centripetal Force
- Example of Centripetal Force
- What is Centrifugal Force?
- Calculating Centrifugal Force
- Examples of Centrifugal Force in daily life:
- Difference between Centripetal and Centrifugal Force:
- Solved Example of Centripetal and Centrifugal Force
What is the Centripetal Force?
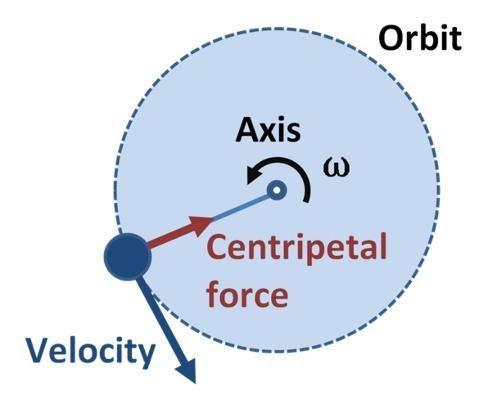
Centripetal Force is the force that keeps an object moving in a circular path.
It always acts towards the centre of the circle and continuously changes the direction of the object's velocity.
Examples:
- Tension in a string when a stone is whirled in a circle
- Gravitational force keeping planets in orbit
- Friction acting on a car while taking a circular turn
Formula:
$F=\frac{m v^2}{r}$
where
$m$ = mass of the object
$v=$ speed
$r=$ radius of the circular path
If a body of mass $m$ is moving in a circle of radius $r$ with angular velocity $\omega$, then its centripetal force is:
$
F=m \omega^2 r
$
Also read -
Calculating Centripetal Force
The formula to calculate centripetal force is defined as the ratio of the product of mass (in kg) and square of the velocity of the object (in meters per second) to the radius of the circular path ( in meters) in which it is moving. As it is a force, the unit of Centripetal force is Newton (N).
$F=m v^2 / r$
where, $\mathrm{F} \rightarrow$ Centripetal Force
$\mathrm{m} \rightarrow$ Mass of the Object
$v \rightarrow$ Velocity of the Object
$r \rightarrow$ Radius of the Circular Path
Example of Centripetal Force
Let’s see some common examples of centripetal force, in order to understand its applications more correctly.
-
Spinning a ball tied to a string:- In this case, when the ball tied to the string rotates in a circular motion, the centripetal force is provided by the tension on the string which pulls the ball towards the center.
-
Planets revolving around the sun:- All the planets revolve around the sun due to the centripetal force provided by the gravity of the sun which pulls all the planets towards it
-
A car turning at a curve:- A traveling car, taking a turn at a curve on the road experiences the centripetal force provided by the friction between the road and the wheels of the car.
-
Merry-go-round:- A child riding on a merry-go-round experiences a centripetal force through the support which holds the child from being thrown out.
-
Electrons revolving around the nucleus:- An electron does not fall into the nucleus in spite of strong nuclear attraction due to the centripetal force provided by the electrostatic attraction between the electron and the nucleus.
|
Related Topics, |
What is Centrifugal Force?
Centrifugal force is defined as a fictitious force acting away from the center of a circular path in which an object is moving.
Let's understand this definition more deeply with the help of an example. Assume a car with a passenger in it is traveling on a straight road. Suddenly, a left turn arrives and the car turns in the left direction.

Centrifugal Force
As the car is moving in a circular path the force experienced by the car is the centripetal force which is towards the center of the circular turn but the force experienced by the passenger within the car is towards the right direction which pushes him outside the car. This outward fictitious force experienced by the passenger due to inertia is known as Centrifugal Force.
Centrifugal force only comes into play when there is a centripetal force acting on an object.
Calculating Centrifugal Force
The formula to calculate Centrifugal force is defined as the negative ratio of the product of mass (in kg) and square of the velocity of the object (in meters per second) to the radius of the circular path ( in meters) in which it is moving. As it is a force, the unit of the centrifugal force is Newton (N).
$$
\mathrm{Fc}=-\mathrm{mv}^2 / \mathrm{r}
$$
where Fc $\rightarrow$ Centripetal Force
$\mathrm{m} \rightarrow$ Mass of the Object
$v \rightarrow$ Velocity of the Object
$r \rightarrow$ Radius of the Circular Path
The formula for centrifugal force is the same as that of centripetal force but with a negative sign as the centrifugal force is directed outward from the center.
Examples of Centrifugal Force in daily life:
Let’s see some common examples of Centrifugal force, in order to understand its applications more correctly.
-
The force experienced by a passenger traveling in a car turning at a curved path is Centrifugal force.
-
A boy rotating a ball tied through a string, the outward force exerted on his hands is centrifugal force.
-
As the centrifugal force acting on an object in the equator is greatest, the earth is flattened at the pole and bulged at the equator.
Also, check-
Difference between Centripetal and Centrifugal Force:
The concept of centripetal force and centrifugal force is often confused, they are closely related to each other.. To understand them more correctly, here are some detailed differences between them.
|
CENTRIPETAL FORCE |
CENTRIFUGAL FORCE |
|
|
|
|
|
|
|
|
|
|
|
|
NCERT Physics Notes :
Solved Example of Centripetal and Centrifugal Force
Q.1 A stone of mass 0.5 kg is tied to a string and rotated in a horizontal circle of radius 2 m with a speed of $4 \mathrm{~m} \mathrm{~s}^{-1}$. Find the centripetal force.
Solution:
Given:
$
\begin{aligned}
& m=0.5 \mathrm{~kg} \\
& r=2 \mathrm{~m} \\
& v=4 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
$
Formula:
$
\begin{gathered}
F_c=\frac{m v^2}{r} \\
F_c=\frac{0.5 \times(4)^2}{2}=\frac{0.5 \times 16}{2}=4 \mathrm{~N}
\end{gathered}
$
Answer:
Centripetal force $=4 \mathrm{~N}$
Q.2 A body of mass 1 kg moves in a circular path of radius 0.5 m with angular velocity $6 \mathrm{rad} \mathrm{s}^{-1}$. Find the centripetal force.
Solution:
Given:
$
\begin{aligned}
& m=1 \mathrm{~kg} \\
& r=0.5 \mathrm{~m} \\
& \omega=6 \mathrm{rad} \mathrm{~s}^{-1}
\end{aligned}
$
Formula:
$
\begin{gathered}
F_c=m \omega^2 r \\
F_c=1 \times(6)^2 \times 0.5=18 \mathrm{~N}
\end{gathered}
$
Answer:
Centripetal force $=18 \mathrm{~N}$
Q.3 A person of mass 60 kg sits in a car moving in a circular track of radius 30 m with speed $10 \mathrm{~m} \mathrm{~s}^{-1}$. Find the centrifugal force experienced by the person.
Solution:
Given:
$
\begin{aligned}
& m=60 \mathrm{~kg} \\
& r=30 \mathrm{~m} \\
& v=10 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
$
Formula:
$
\begin{gathered}
F=\frac{m v^2}{r} \\
F=\frac{60 \times(10)^2}{30}=200 \mathrm{~N}
\end{gathered}
$
Answer:
Centrifugal force $=200 \mathrm{~N}$
Frequently Asked Questions (FAQs)
The center directed force acting perpendicular to the direction of motion of an object moving in a circular path is defined as centripetal force. The formula to calculate centripetal force is
F=mv2/r
A fictitious force acting away from the center of a circular path in which an object is moving is known as centrifugal force. The formula to calculate centrifugal force is
Fc =-mv2/r
Mass of car, m = 500kg
Velocity of car, v = 20 m/sec
Radius of the circular path, r = 4m
To calculate :- Centripetal Force
Formula for centripetal force is
F=mv2/r
F=50000 N
Hence, the Centripetal force experienced by the car is 50,000 N.
Some common example of centripetal force of centripetal force are.
A child riding on a merry go round experiences a centripetal force through the support which hold the child from being thrown out.
A car turning at a curved path, experiences the centripetal force due to the friction between the wheels and the road.
The centrifugal force experienced by the body is -20N because centrifugal force is same as that of centripetal force but with a negative sign as the centrifugal force is directed outward from the center and centripetal force is directed toward the center.
