Fraunhofer Diffraction By A Single Slit

Fraunhofer diffraction by a single slit refers to the pattern of light observed when a wave passes through a narrow aperture and spreads out. This phenomenon occurs due to the wave nature of light and results in a distinctive pattern of bright and dark fringes on a screen. Understanding Fraunhofer diffraction is fundamental in optics, influencing technologies such as optical instruments and laser design. In real life, it helps in improving the resolution of microscopes and telescopes and is applied in the study of wave behaviour in various fields, including acoustics and quantum mechanics. This article explores the principles behind Fraunhofer diffraction and its practical applications.

This Story also Contains

1. Fraunhofer Diffraction by a Single Slit
2. Solved Examples Based on Fraunhofer Diffraction by a Single Slit
3. Summary

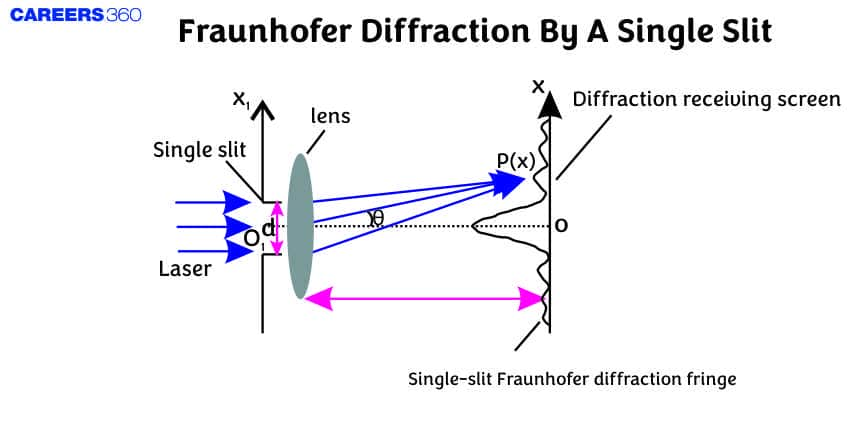
Fraunhofer Diffraction by a Single Slit

Fraunhofer diffraction by a single slit refers to the pattern of light observed when a wave passes through a narrow aperture and spreads out. This phenomenon occurs due to the wave nature of light and results in a distinctive pattern of bright and dark fringes on a screen, known as the diffraction pattern. The central maximum is the brightest and widest, with subsequent maxima and minima decreasing in intensity and width.

let's assume a plane wavefront is incident on a slit AB (of width b). Each and every part of the exposed part of the plane wavefront (i.e. every part of the slit) acts as a source of secondary wavelets spreading in all directions. The diffraction is obtained on a screen placed at a large distance. (In practice, this condition is achieved by placing the screen at the focal plane of a converging lens placed just after the slit).

• The diffraction pattern consists of a central bright fringe (central maxima) surrounded by dark and bright lines (called secondary minima and maxima).
• At point O on the screen, the central maxima is obtained. The wavelets originating from points A and B meet in the same phase at this point, hence at O, intensity is maximum

Secondary Minima

In Fraunhofer diffraction by a single slit, secondary minima are the points where the intensity of the diffracted light falls to zero between the central maximum and subsequent maxima. These minima occur due to destructive interference, where the light waves cancel each other out.

For obtaining the nth secondary minima at P on the screen, the path difference between the diffracted waves

$\Delta x=b \sin \theta=n \lambda$

Angular position of nth secondary minima:

$\sin \theta \approx \theta=\frac{n \lambda}{b}$

Distance of nth secondary minima from central maxima:

$\begin{array}{r}x_n=D \cdot \theta=\frac{n \lambda D}{b} \quad \text { where } \mathrm{D}=\text { Distance between slit and screen. } \\ f \approx D=\text { Focal length of converging lens. }\end{array}$

Secondary Maxima

Secondary maxima in Fraunhofer diffraction by a single slit refer to the less intense bright fringes that appear between the primary maxima and the dark fringes in a diffraction pattern. When monochromatic light passes through a single slit and is projected onto a distant screen, the wavefronts interfere, creating a series of bright and dark bands. The central bright fringe, or primary maximum, is the most intense, while the secondary maxima are smaller peaks of intensity located on either side of the central maximum.

For nth secondary maxima at P on the screen.

Path difference $\Delta x=b \sin \theta=(2 n+1) \frac{\lambda}{2} ;$ where $\mathrm{n}=1,2,3 \ldots \ldots$.

(i) Angular position of nth secondary maxima

$\sin \theta \approx \theta \approx \frac{(2 n+1) \lambda}{2 b}$

(ii) Distance of nth secondary maxima from central maxima:

$x_n=D \cdot \theta=\frac{(2 n+1) \lambda D}{2 b}$

Central Maxima

The central maxima in Fraunhofer diffraction by a single slit is the brightest and widest part of the diffraction pattern observed on a screen. When light passes through a narrow slit, it spreads out and forms a series of bright and dark fringes. The central maxima are located at the midpoint directly opposite the slit and are significantly more intense than the subsequent fringes. The central maxima lie between the first minima on both sides.

(i) The Angular width d central maxima $=2 \theta=\frac{2 \lambda}{b}$
(ii) Linear width of central maxima $=2 x=2 D \theta=2 f \theta=\frac{2 \lambda f}{b}$

Intensity Distribution

The intensity distribution in Fraunhofer diffraction by a single slit is characterized by a central maximum flanked by a series of progressively fainter secondary maxima and minima. This pattern results from the interference of light waves emanating from different parts of the slit, creating regions of constructive and destructive interference. if the intensity of the central maxima is $I_0$ then the intensity of the first and secondary maxima are
found to be $\frac{I_0}{22}$ and $\frac{I_0}{61}$. Thus diffraction fringes are of unequal width and unequal intensities.

(i) The mathematical expression for in-intensity distribution on the screen is given by:

$I=I_o\left(\frac{\sin \alpha}{\alpha}\right)^2$ where $\alpha$ is just a convenient connection between the angle $\theta$ that locates a point on the viewing screening and light intensity I.

$\phi=$ Phase difference between the top and bottom ray from the slit width b.
Also $\alpha=\frac{1}{2} \phi=\frac{\pi b}{\lambda} \sin \theta$.

(ii) As the slit width increases relative to wavelength the width of the control diffraction maxima decreases that is, the light undergoes less flaring by the slit. The secondary maxima also decreases in width and becomes weaker.

(iii) If $b \gg \lambda \lambda$, the secondary maxima due to the slit disappear; we then no longer have single-slit diffraction.

Recommended Topic Video

Solved Examples Based on Fraunhofer Diffraction by a Single Slit

Example 1: A single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000 Å and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is :

1) 3 mm

2) 9 mm

3) 4.5 mm

4) 1.5 mm

Solution:

Fraunhofer Diffraction

$b \sin \theta=n \lambda$

wherein

Condition of n^th minima.

$\begin{aligned} & b=\text { slit width } \\ & \theta=\text { angle of deviation }\end{aligned}$

$\begin{aligned} & \mathrm{a}=0.1 \mathrm{~mm}=10^{-4} \mathrm{~cm} \\ & \lambda=6000 \AA=6 \times 10^{-7} \mathrm{~cm} \\ & \mathrm{D}=0.5 \mathrm{~m} \\ & \text { for } 3^{\text {rd }} \text { dark bond, } a \sin \theta=3 \lambda \\ & \sin \theta=\frac{3 \lambda}{a}=\frac{x}{D} \\ & \therefore x=\frac{3 \lambda D}{a} \\ & x=\frac{3 \times 6 \times 10^{-7} \times 0.5}{10^{-4}} \\ & \mathrm{x}=9 \mathrm{~mm}\end{aligned}$

Hence, the answer is the option (2).

Example 2: A parallel beam of electrons travelling in x-direction falls on a slit of width d (see figure). If after passing the slit, an electron acquires momentum p_y in the y-direction then for a majority of electrons passing through the slit (h is Planck’s constant) :

$\begin{aligned} & \text { 1) }\left|P_y\right| d \simeq h \\ & \text { 2) }\left|P_y\right| d>h \\ & \text { 3) }\left|P_y\right| d<h \\ & \text { 4) }\left|P_y\right| d>>h\end{aligned}$

Solution:

Fraunhofer Diffraction
$
b \sin \theta=n \lambda
$
wherein
Condition of $\mathrm{n}^{\text {th }}$ minima.
$b=$ slit width
$\theta=$ angle of deviation
$
d \sin \theta=\lambda \Rightarrow \sin \theta=\frac{\lambda}{d}<1
$

$\begin{aligned} & \lambda<d\left[\lambda=\frac{h}{\left[P_y\right]}\right] \\ & \frac{h}{\left[P_y\right]}<d \\ & \therefore \quad h<\left|P_y\right| d \\ & \left|P_y\right| d<h\end{aligned}$

Hence, the answer is the option (3).

Example 3: Light of wavelength 550 nm normally falls on a slit of width $22.0 \times 10^{-5}$ cm. The angular position of the second minima from the central maximum will be (in radians):

1) $\frac{\pi}{12}$
2) $\frac{\pi}{8}$
3) $\frac{\pi}{6}$
4) $\frac{\pi}{4}$

Solution:

Fraunhofer Diffraction
$
b \sin \theta=n \lambda
$

Condition of $\mathrm{n}^{\text {th }}$ minima.
$b=$ slit width
$\theta=$ angle of deviation
for second minima
$
\begin{aligned}
& b \sin \theta=2 \lambda \\
& \Rightarrow \sin \theta=\frac{2 \lambda}{b}=\frac{2 \times 550 \times 10^{-9}}{22 \times 10^{-7}}=0.50 \\
& \theta=\frac{\pi}{6}
\end{aligned}
$

Hence, the answer is the option (3).

Example 4: In an experiment of the single slit diffraction pattern, the first minimum for red light coincides with the first maximum of some other wavelength. If wavelengths of red light is 6600 Å , then the wavelength of the first maximum will be :

1) 3300 Å

2) 4400 Å

3) 5500 Å

4) 6600 Å

Solution:

$
b \sin \theta=n \lambda
$
$b=$ slit width
$
\theta=\text { angle of deviation }
$

For first maxima
$
b \sin \theta=\frac{3 \lambda}{2} \ldots \ldots .
$

For the first minima of red light
$
\begin{aligned}
& b \sin \theta=\lambda_{\text {red }} \\
& \Rightarrow \lambda_{\text {red }}=\frac{3 \lambda}{2} \\
& \text { or } \lambda=\frac{2 \lambda}{3} \text { Red }=4400 A^{\circ}
\end{aligned}
$

Hence, the answer is the option (2).

Example 5: If $I_0$ is the intensity of the principal maximum in the single slit diffraction pattern, then what will be its intensity when the slit width is doubled?

1) $I_0$
2) $I_0 / 2$
3) $2 I_0$
4) $4 I_0$

Solution:

Since slit width is double amplitude is also doubled. Hence the intensity of maxima becomes 4 times.

Hence, the answer is the option (4).

Summary

Fraunhofer diffraction by a single slit produces a pattern of bright and dark fringes due to the wave nature of light, with the central maximum being the brightest and widest. The intensity distribution features secondary maxima and minima caused by constructive and destructive interference, respectively. The pattern's characteristics, including angular positions and intensities of minima and maxima, depend on factors such as slit width and light wavelength. This phenomenon has practical applications in improving optical instruments and studying wave behaviour in various fields.