Magnetic Field On The Axis Of Circular Current Loop

The magnetic field on the axis of a circular current loop is a fundamental concept in electromagnetism, describing the magnetic influence generated by an electric current flowing through a looped conductor. This field is concentrated along the axis perpendicular to the plane of the loop and diminishes with distance from the centre. Understanding this phenomenon is crucial for various applications, such as in designing electromagnets, inductors, and MRI machines, where controlled magnetic fields are required. In real life, it can be seen in the working of wireless charging pads, where magnetic fields are used to transfer energy between a charger and a device through inductive coupling, a principle derived from circular current loops. This concept also plays a role in electric motors, where magnetic fields interact to produce rotational motion.

The Magnetic Field on the Axis of the Circular Current Carrying Loop

In the figure, it is shown that a circular loop of radius R carries a current $I$. Application of Biot-Savart law to a current element of length $dl$ at angular position $\theta$ with the axis of the coil. the current in the segment $d\ell$ causes the field $d\overline{B}$ which lies in the $x$-y plane as shown below.

Another symetric $d{\overline{\ell }}^{\prime }$ element that is diametrically opposite to previously $d\ell$ element cause $d\overrightarrow{B^{\prime }}$.
Due to symmetry the components of $d\overrightarrow{B}$ and $d\overrightarrow{B^{\prime }}$ perpendicular to the x -axis cancel each other. i.e., these components add to zero.
The x-components of the $d\overrightarrow{B}$ combine to give the total field $\overrightarrow{B}$ at point $P$.

We can use the law of Biot-Savart to find the magnetic field at a point P on the axis of the loop, which is at a distance $x$ from the centre. $d\overline{\ell }$ and $\hat{r}$ are perpendicular and the direction of field $d\overline{B}$ caused by this particular element $d\overline{\ell }$ lies in the x-y plane.

The magnetic field due to the current element is

$\mathrm{dB}=\frac{{\mu }_{\mathrm{o}}\mathrm{I}}{4\pi }\int \frac{\mathrm{d}\mathbf{l}\times \hat{\mathbf{r}}}{{\mathrm{r}}^2}$
Since $r^2=x^2+R^2$
the magnitude $dB$ of the field due to element $d\overline{\ell }$ is:

$dB=\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}$
The components of the vector $dB$ are

$\begin{array}{rl}& d{B}_x=dB\sin \theta =\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}\frac{R}{{(x^2+R^2)}^{1/2}}\dots (\\ & d{B}_y=dB\cos \theta =\frac{{\mu }_{0}I}{4\pi }\frac{d\ell }{(x^2+R^2)}\frac{x}{{(x^2+R^2)}^{1/2}}\dots \end{array}$
Total magnetic field along axis $=B_{\text{axis }}=\int d{B}_x=\int dB\sin \theta$

$\because \int d{B}_y=\int dB\cos \theta =0$
Everything in this expression except $d\overrightarrow{\ell }$ is constant and can be taken outside the integral.

The integral $d\overrightarrow{\ell }$ of is just the circumference of the circle, i.e., $\int d\ell =2\pi R$
So, we get
$\Rightarrow B_{\text{axis }}=\frac{{\mu }_{0}I{R}^2}{2{(x^2+R^2)}^{3/2}}$ (on the axis of a circular loop)
- If $x\gg R$, then $B=\frac{{\mu }_{0}I{R}^2}{2x^3}$.
- At centre.

$x=0\Rightarrow B_{\text{centre }}=\frac{{\mu }_0}{4\pi }\cdot \frac{2\pi \mathrm{N}i}{R}=\frac{{\mu }_{0}Ni}{2R}=B_{max}$

Recommended Topic Video

Solved Examples Based on Magnetic Field on the Axis of Circular Current Loop

Example 1: The magnetic field due to a current carrying a circular loop of radius 3 cm at a point on the axis at a distance of 4 cm from the centre is $54\mu T$. What will be its value (in $\mu T$ ) at the centre of the loop?

1) 250

2) 150

3) 125

4) 75

Solution:

Magnetic Field at the axis due to circular current carrying wire
$B_{\text{axis }}=\frac{{\mu }_0}{4\pi }\cdot \frac{2\pi Ni{r}^2}{{(x^2+r^2)}^{\frac{3}{2}}}$

wherein
N is the number of turns in the coil
Magnetic Field due to Circular Current at the centre -

$B_{\text{centre }}=\frac{{\mu }_0}{4\pi }\frac{2\pi Ni}{r}=\frac{{\mu }_{0}Ni}{2r}$

wherein

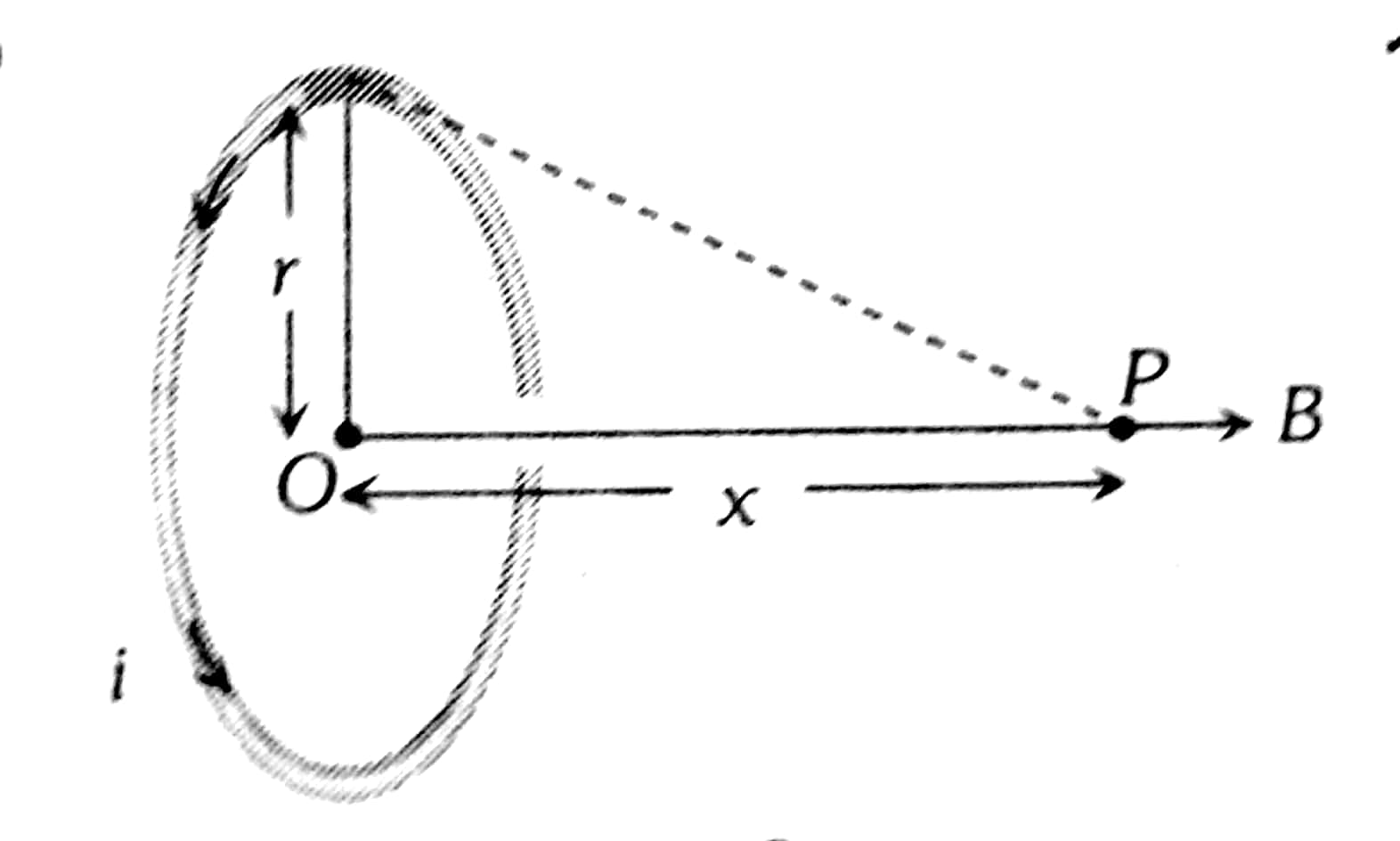
: Field along axis of coil $B=\frac{{\mu }_{0}i{R}^2}{2{(R^2+x^2)}^{3/2}}$
At the centre of coil, $B^{\prime }=\frac{{\mu }_{0}i}{2R}$

$\begin{array}{ll}\therefore & \frac{B^{\prime }}{B}=\frac{{\mu }_{0}i}{2R}\times \frac{2{(R^2+x^2)}^{3/2}}{{\mu }_{0}i{R}^2}=\frac{{(R^2+x^2)}^{3/2}}{R^3}\\ \therefore & B^{\prime }=\frac{B\times {(R^2+x^2)}^{3/2}}{R^3}\\ \therefore & =\frac{54\times {[(3{)}^2+(4{)}^2]}^{3/2}}{(3{)}^3}=\frac{54\times 125}{27}\end{array}$

or $B^{\prime }=250\mu T$

Hence, the answer is the option (1).

Example 2: Directions: Question are based on the following paragraph.
A current loop $ABCD$ is held fixed on the plane of the paper as shown in the figure. The arcs $BC($ radius $=b)$ and $DA($ radius $=a)$ of the loop are joined by two straight wires $AB$ and $CD$. A steady current $I$ is flowing in the loop. Angle made by $AB$ and $CD$ at the origin $O$ is ${30}^{\circ }$. Another straight thin wire with steady current $I_1$ flowing out of the plane of the paper is kept at the origin.

Due to the presence of the current $I_1$ at the origin

1) the forces on $AB$ and $DC$ are zero
2) the forces on $AD$ and $BC$ are zero
3) the magnitude of the net force on the loop is given by $\frac{I_{1}I}{4\pi }{\mu }_0[2(b-a)+\frac{\pi }{3}(a+b)]$
4) the magnitude of the net force on the loop is given by $\frac{{\mu }_{0}I{I}_1}{24ab}(b-a)$

Solution:

Magnetic Field due to Circular Current at the centre

If a coil of radius r is carrying current I then the magnetic field at a distance X from its centre is:

$B_{\text{centre }}=\frac{{\mu }_0}{4\pi }\frac{2\pi Ni}{r}=\frac{{\mu }_{0}Ni}{2r}$

wherein

The force on AD and BC due to current $I_1$ is zero.
This is because the directions of current element $I\overrightarrow{dI}$ and magnetic field $\overrightarrow{B}$ are parallel.

Hence, the answer is the option (2).

Example 3: A thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of $40\pi {\mathrm{rad}}^{-1}$ about its axis, perpendicular to its plane. If the magnetic field at its center is $3.8\times {10}^{-9}\mathrm{T}$, then the charge carried by the ring is close to $({\mu }_0=4\pi \times {10}^{-7}N/A^2)$.

1) $7\times {10}^{-6}\mathrm{C}$
2) $3\times {10}^{-5}\mathrm{C}$
3) $2\times {10}^{-6}\mathrm{C}$
4) $4\times {10}^{-5}\mathrm{C}$

Solution:

The magnetic field at the centre of a current-carrying ring, $B=\frac{{\mu }_{0}i}{2R}$

$\begin{array}{rl}& i=\frac{q}{T}\\ & T=\frac{2\pi }{\omega }\\ & B=\frac{{\mu }_{0}qw}{2R(2\pi )}\\ & \Rightarrow q=\frac{4\pi RB}{{\mu }_{0}w}\\ & \Rightarrow q=3\times {10}^{-5}C\end{array}$

Hence, the answer is the Option (2).

Example 4: A current $i$ ampere flows along an infinitely long straight thin-walled tube, and then the magnetic induction at any point inside the tube is

1) infinite
2) zero
3) $\frac{{\mu }_0}{4\pi }\cdot \frac{2i}{r}$ tesla
4) $\frac{2i}{r}$ tesla

Solution:

The magnetic field inside a thin hollow cylinder

B=0

wherein

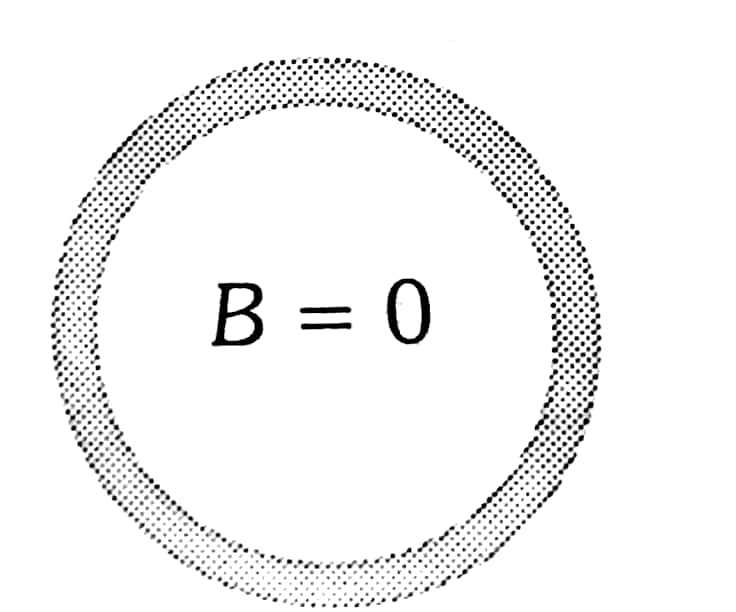
The magnetic field will be zero inside the straight-walled tube according to Ampere's theorem.

Hence, the answer is the option (2).

Example 5: In Fig we can say about the magnetic field

1) Magnetic field is non-uniform

2) The magnetic field is zero

3) The magnetic field is away from the observer

4) Magnetic field is towards the observer

Solution:

As we learned

Out

The magnetic field is towards the observer or perpendicular outward

wherein

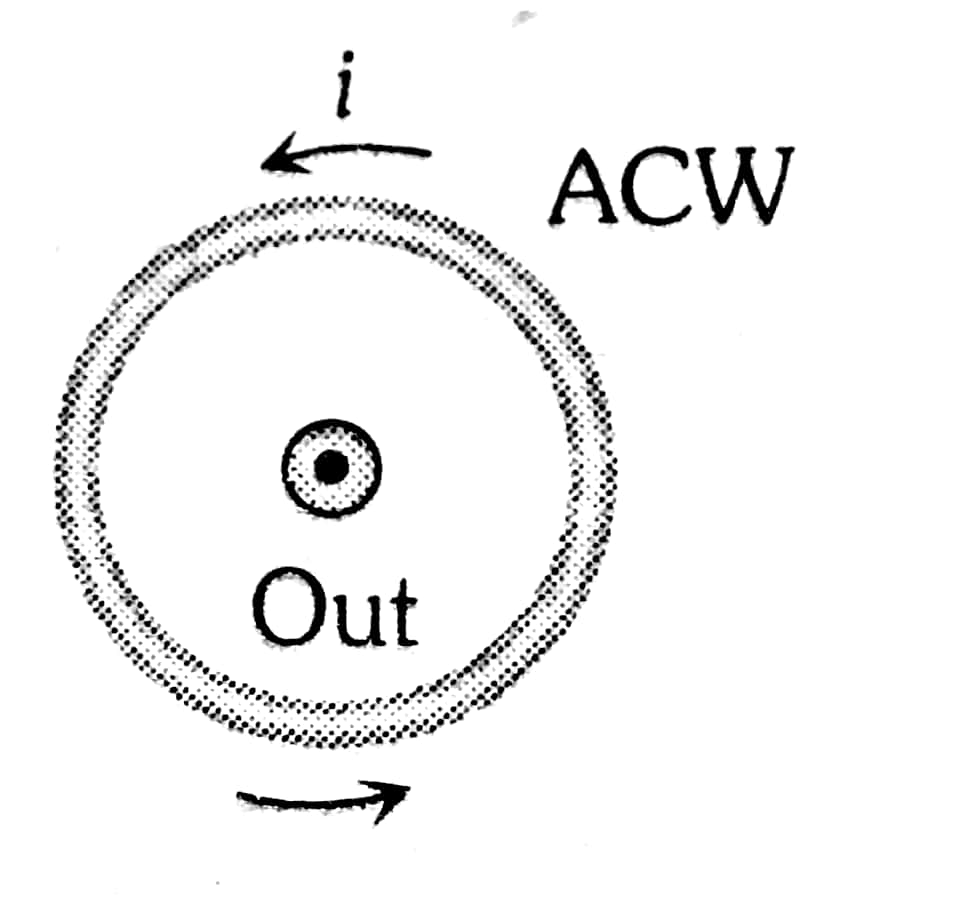
If $⨀$ is given i.e. magnetic field is towards observer or $\perp$ outwards.

Hence, the answer is the option (4).

Summary

The magnetic field on the axis of a circular current loop is determined using the Biot-Savart law, where the field is strongest at the centre and diminishes with distance. The magnetic field at any point on the axis depends on the radius of the loop and the current flowing through it. Several examples demonstrate how this principle applies, including calculating the field at the centre and along the axis of a current-carrying loop, and the influence of currents in specific geometric setups, such as thin rings and straight wires.