Important Terms In Simple Harmonic Motion

Periodic motion characterises all simple harmonic motions. It moves back and forth between its extreme and mean positions, oscillating. The oscillating object experiences the restoring force throughout the oscillation. This restoring force is equivalent to the displacement from the object's mean position but has a direction that is opposite to that of the displacement.

This Story also Contains

1. Amplitude
2. Time Period
3. Solved Examples Based on Terms associated with SHM
4. Summary

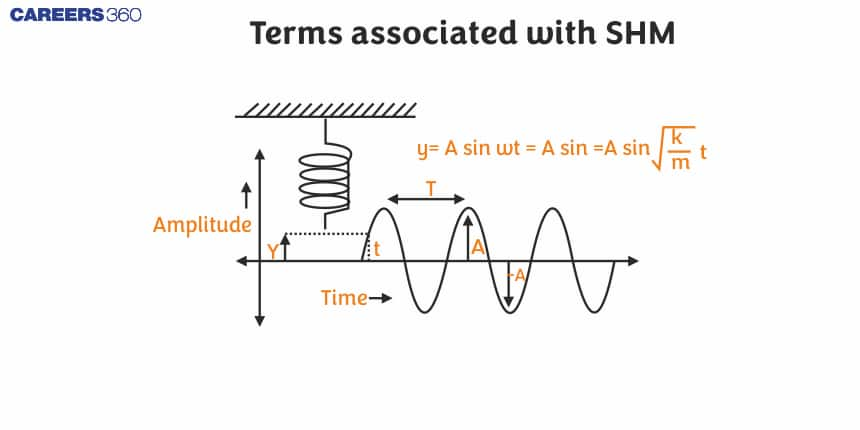
In this article, we will discuss the main concepts of terms associated with SHM, as well as find its main formulas and discuss their use in different physical situations. At the same time, it helps them appreciate that S.H.M. is not just about passing exams but very beautiful and everywhere in nature. This topic is the part of chapter Oscillations and Waves, which is a crucial chapter in Class 11 physics. It is not only important for state board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), four questions have been asked on this concept. And three questions have been asked for NEET.

Now, let's read the entire article to know the terms associated with SHM which are amplitude, frequency, phase difference and more.

Amplitude

We know that the displacement of a particle in SHM is given by:

x=ASin(ωt+ϕ)

The quantity A is called the amplitude of the motion. It is a positive constant which represents the magnitude of the maximum displacement of the particle from the mean position in either direction.

Time Period

In SHM, a particle repeats its motion after a fixed interval of time. And this time interval after which the particle repeats its motion is called time period. It is denoted by T.

Time period is also defined as the time taken to complete one oscillation. And after one time period, both displacement and velocity of the particle are repeated.

We know that-

x=ASin(ωt+ϕ)

If a motion is periodic with a period T, then the displacement x (t) must return to its initial value after one period of the motion; that is, x (t) must be equal to x (t + T ) for all t and velocity v(t) must also return to its initial value, i.e., v(t) must be equal to v(t+T). So,

x(t)=x(t+T)⇒ASin(ωt+ϕ)=ASin[ω[t+T]+ϕ]⇒Sin(ωt+ϕ)=Sin[ω[t+T]+ϕ]

And
v(t)=v(t+T)⇒AωCos(ωt+ϕ)=AωCos[ω[t+T]+ϕ]⇒Cos(ωt+ϕ)=Cos[ω[t+T]+ϕ]

As we know both the Sine and Cosine function repeats themselves when their argument increases by 2π,i.e.,

ωt+ϕ+2π=ω(t+T)+ϕ⇒2π=Tω⇒T=2πω=2πmk
where k= force or spring constant and m= mass

Time period can also be written as

T=2πω=2πmk=2πm Force displacement =2πm× displacement m× acceleration ⇒T=2π displacement acceleration

Frequency

The reciprocal of T gives the number of repetitions that occur per unit time. This quantity is called the frequency of the periodic motion. It is denoted by f.

f=1T=ω2π=12πkm
⇒ω=2πf; where ω is angular frequency

• The unit of frequency is s−1 or Hertz(Hz).

Phase

• The quantity (ωt+Δϕ) is called the phase.
• It determines the status of the particle in simple harmonic motion.
• If the phase is zero at a certain instant, then:

x=ASin(ωt+ϕ)=0 and v=AωCos(ωt+ϕ)=Aω

which means that the particle is crossing the mean position and is going towards the positive direction.

Fig:- Status of the particle at different phases

Phase constant

• The constant ϕ is called the phase constant (or phase angle).

• The value of ϕ depends on the displacement and velocity of the particle at t=0 or we can say the phase constant signifies the initial conditions.

• Any instant can be chosen as t = 0 and hence the phase constant can be chosen arbitrarily.

Recommended Topic Video

Solved Examples Based on Terms associated with SHM

Example 1: A 1×10−20 kg particle is vibrating with simple harmonic motion with a period of 1×10−5 s and a maximum speed of 1×103 m/s. The maximum displacement (in mm) of the particle is:

1) 1.59

2) 1.0

3) 100

4) None of these

Solution:

Amplitude

The maximum displacement of a particle from its mean position where it will come to rest or from where it started with zero initial speed.

wherein

At such point kinetic energy = 0

Potential energy is maximum.

vmax=aω=a×2πT⇒a=vmax×T2πA=1.00×103×(1×10−5)2π=1.59 mm

Hence, the answer is option (1).

Example 2: A particle oscillates according to the equation x=7cos⁡0.5πt where t is in second. The point moves from the position of equilibrium to maximum displacement in time (in seconds)

1) 4

2) 2.0

3) 1

4) 0.5

Solution:

From the given equation,

ω=2πT=0.5π⇒T=4s

Time taken from mean position to the maximum displacement =14T=1 s

Hence, the answer is option (3).

Example 3: A simple harmonic oscillator has an amplitude α and time period T. The time required (in seconds) by it to travel from x=α to x=α2 is:

1) T/3

2) T/2

3) T

4) T/6

Solution:

Time Period

Since all periodic motions repeat themselves in equal time intervals. This minimum time interval is known as time period for oscillation.

It is required to calculate the time from the extreme position. Hence, in this case, the equation for the displacement of a particle can be written as

x=asin⁡(ωt+π2)=acos⁡ωt⇒a2=acos⁡ωt⇒ωt=π3⇒2πT⋅t=π3⇒t=T6

Hence, the answer is the option (4).

Example 4: A particle executes simple harmonic motion (amplitude =A ) between x=−A and x=+A. The time taken for it to go 0 to A2 is T1 and to go from 2― to A is T2. Then

1) T1<T2
2) T1>T2
3) T1=T2
4) T1=2T2

Solution:

Since all periodic motions repeat themselves in equal time intervals. This minimum time interval is known as time period for oscillation. It is denoted by T.

Using x=Asin⁡ωt
For x=A2sin⁡ωT1=12⇒T1=π6ω
For x=A1sin⁡ω(T1+T2)=1⇒T1+T2=π2ω
⇒T2=π2ω−T1=π2ω−π6ω=π3ω
i.e T1<T2

Hence, the answer is the option (1).

Example 5: The correct figure that shows, schematically, the wave pattern produced by the superposition of two waves of frequencies 9 Hz and 11 Hz, is :

1)

2)

3)

4)

Solution:

Angular frequency

The number of revolutions (expressed in radians) performed per unit time is known as Angular Frequency.

wherein

It is represented by w=2πT
ν0=(11−9)=2HzT0=12sec=0⋅5sec

Hence, the answer is option (4).

Summary

In summary, the meaning of the commonly used terminology and ideas for Simple Harmonic Motion (S.H.M.) helps in describing how oscillating systems move. This is what makes it possible for people to understand S.H.M., hence coming up with solutions to various oscillatory motion physics problems. Therefore, having knowledge about these concepts will enable individuals to evaluate and predict the performance of simple harmonic motion systems with more precision.