Born Habers Cycle

The Born-Haber cycle is a thermochemical cycle used in the examination of the different stages by which an ionic compound is formed from its elements. It is named for Max Born and Fritz Haber. This cycle makes use of Hess's Law in the estimation of lattice energy, which represents the energy change upon crystalline lattice formation from gaseous ions. The cycle outlines the various steps in the formation of an ionic solid: sublimation, ionization, dissociation, electron affinity, and lattice formation. Each of these steps has an associated enthalpy change, so their summation will give the net enthalpy change of formation of the ionic compound.

This Story also Contains

1. Born-Haber Cycle
2. Some Solved Examples
3. Summary

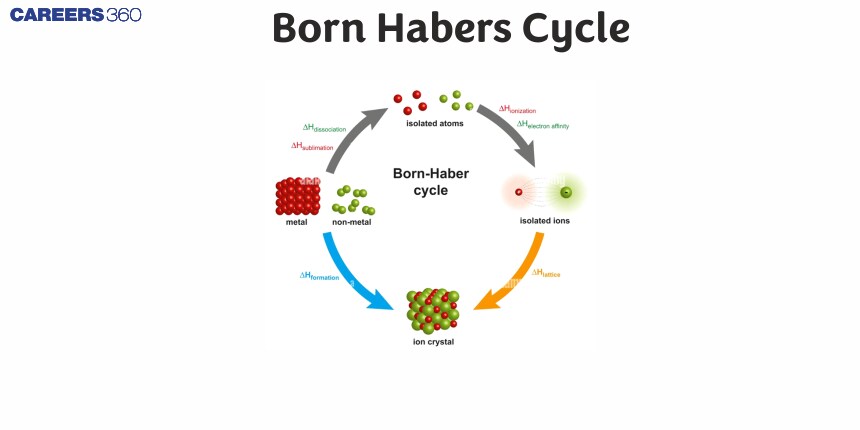
Born-Haber Cycle

There are several important concepts to understand before the Born-Haber Cycle can be applied to determine the lattice energy of an ionic solid; ionization energy, electron affinity, dissociation energy, sublimation energy, heat of formation, and Hess's Law.

The diagram below is the Born-Haber cycle for the formation of an ionic compound from the reaction of an alkali metal (Li, Na, K, Rb, Cs) with a gaseous halogen (F₂, Cl₂). The Born-Haber thermochemical cycle is named after the two German physical chemists, Max Born and Fritz Haber, who first used it in 1919.

Recommended topic video on ( Born Habers Cycle)

Some Solved Examples

Example 1: Enthalpies of solution of $\mathrm{BaCl}_2$ and $\mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}$ are -19 KJ/mol and 7 KJ/mol, respectively. Calculate enthalpy of hydration (in KJ/mol) of $\mathrm{BaCl}_2$ to $\mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}$.

(Response should be an integer value)

1)-12

2)12

3) -26

4)26

Solution

Enthalpy of hydration of BaCl₂ is given as,

$\mathrm{BaCl}_{2(\mathrm{~s})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{l})} \rightarrow \mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{s})} \quad \Delta_{\text {hyd }} \mathrm{H}=?$

We have given the enthalpy of the solution of BaCl₂ and BaCl₂.2H₂O.

(i). $\mathrm{BaCl}_{2(\mathrm{~s})}+\mathrm{aq}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{l})} \rightarrow \mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{aq})} \quad \Delta \mathrm{H}=-19 \mathrm{KJ} / \mathrm{mol}$(ii). $\mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{s})}+\mathrm{aq} \rightarrow \mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{aq})} \quad \Delta \mathrm{H}=+7 \mathrm{KJ} / \mathrm{mol}$

Subtracting equation (ii) from (i) we get the resultant equation as,

$\mathrm{BaCl}_{2(\mathrm{~s})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{l})} \rightarrow \mathrm{BaCl}_2 \cdot 2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{s})} \quad \Delta \mathrm{H}=(-19-7) \mathrm{KJ} / \mathrm{mol}$

The above reaction is the Enthalpy of hydration of BaCl₂.

So,

$\Rightarrow \Delta \mathrm{H}=-26 \mathrm{KJ} / \mathrm{mol}$

Example 2: Which enthalpy cycle is used to calculate lattice energy?

1)Carnot cycle

2)Haber cycle

3) Born haber cycle

4)Contact process

Solution

Born–Haber cycle applies Hess's law to calculate the lattice energy by comparing the standard enthalpy change of formation of the ionic compound (from the elements) to the enthalpy required to make gaseous ions from the elements.

Hence, the answer is the option (3).

Example 3: The ionization enthalpy of Na⁺ formation from Na is 495.8 kJ mol^-1, while the electron gain enthalpy of Br is -325.0 kJ mol^-1. Given the lattice enthalpy of NaBr is -728.4 kJ mol^-1. The energy for the formation of NaBr ionic solid is (-) _________ $\times 10^{-1} \mathrm{kJmol}^{-1}$

1) 5576

2)5578

3)5574

4)8546

Solution

$\begin{array}{ll}\mathrm{Na}(\mathrm{s}) \longrightarrow \mathrm{Na}^{+}(\mathrm{g}) & \Delta \mathrm{H}=495.8 \\ \frac{1}{2} \mathrm{Br}_2(\ell)+\mathrm{e}^{-} \longrightarrow \mathrm{Br}^{-}(\mathrm{g}) & \Delta \mathrm{H}=-325 \\ \mathrm{Na}^{+}(\mathrm{g})+\mathrm{Br}^{-}(\mathrm{g}) \longrightarrow \mathrm{NaBr}(\mathrm{s}) & \Delta \mathrm{H}=-728.4 \\ \mathrm{Na}(\mathrm{s})+\frac{1}{2} \mathrm{Br}_2(\ell) \longrightarrow \mathrm{NaBr}(\mathrm{s}) & \Delta \mathrm{H}=? \\ \begin{aligned} \Delta \mathrm{H}=495.8-325-728.4 & \\ & =-557.6 \mathrm{~kJ}=-5576 \times 10^{-1} \mathrm{~kJ}\end{aligned}\end{array}$

Answer : 5576

Example 4: The Born-Habers cycle for KCl is evaluated with the following data:

$\Delta_{\mathrm{f}} \mathrm{H}^{\ominus}$ for $\mathrm{KCl}=-436.7 \mathrm{~kJ} \mathrm{~mol}^{-1} ; \Delta_{\text {sub }} \mathrm{H}^{\ominus}$ for $\mathrm{K}=89.2 \mathrm{~kJ} \mathrm{~mol}^{-1} ;$

$\Delta_{\text {ionization }} \mathrm{H}^{\ominus}$ for $\mathrm{K}=419.0 \mathrm{~kJ} \mathrm{~mol}^{-1} ; \Delta_{\text {electron gain }} \mathrm{H}^{\ominus}$ for $\mathrm{Cl}_{(\mathrm{g})}=-348.6 \mathrm{~kJ} \mathrm{~mol}^{-1} ;$

$\Delta_{\text {bond }} \mathrm{H}^{\ominus}$ for $\mathrm{Cl}_2=243.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$

The magnitude of lattice enthalpy of KCl in kJ mol ^-1 is _______(Nearest integer)

1) 718

2)457

3)568

4)245

Solution

The Born Haber cycle is given as

Thus,

$89.2+419+121.5-348-\mathrm{LE}=-436.7$

$\therefore \mathrm{LE}=718.4$

Example 5: The lattice energy of solid NaCl is 200 Kcal/mol. The enthalpy of dissolution of solid NaCl is endothermic to the extent of 1Kcal/mol. If the hydration enthalpy of $\mathrm{Na}^{+}$ and $\mathrm{Cl}^{-}$ are in the ratio of 7:6, then what is the enthalpy of hydration (in Kcal/mol) of sodium ions?

1)107

2) -107

3)-199

4)-92

Solution

As we learned, Enthalpy of Solution = Lattice Energy + Hydration Enthalpy

$\Delta_{\text {sol }} \mathrm{H}=\Delta_{\text {lattice }} \mathrm{H}+\Delta_{\text {hyd }} \mathrm{H}$

Or we can also write it as,

$1=200+\Delta_{\text {hyd }} H$

$\Rightarrow \Delta_{\text {hyd }} \mathrm{H}=-199 \mathrm{kcal} \mathrm{mol}^{-}$

It is given that the ratio of hydration enthalpies of Na⁺ and Cl^- ions is 7:6

Hydration energy of Na+ ions = $\frac{7}{7+6} \times(-199)$ = -107 Kcal/mol

Hence, the answer is the option (2).

Summary

The Born-Haber cycle is the theoretical cycle for the calculation of lattice energy of ionic compounds from Hess' Law. The different steps involved in this cycle are as follows: sublimation of the metal atom, ionization of metal atoms to form cations, dissociation of the nonmetal molecule into atoms, electron affinity of nonmetal atoms to form anions, and lastly, formation of the ionic solid from gaseous ions. The associated enthalpy change is characteristic for each step, and their sum gives the overall enthalpy change in the formation of the ionic compound. This is an important cycle in establishing the formation and stability of the ionic compounds, especially so far as the energy changes involved and the strength of the ionic bonds are concerned.