Analytic Geometry

Geometry and algebra are brought together to produce analytic geometry. Rene Descartes and Fermat were renowned inventors who created the part of algebra known as analytic geometry. Analytic geometry aims to use algebraic equations to present geometric figures in either a two-dimensional or three-dimensional setting. Basic coordinate geometry formulas, equations for lines and curves, axes that can be translated and rotated, and three-dimensional geometry principles are all included in analytic geometry. "Coordinate Geometry" is another word that is used to describe analytic geometry.

What Is Analytic Geometry?

The branch of algebra known as analytical geometry allows one to identify a point on a plane using an ordered pair of numbers known as coordinates. This is also referred to as Cartesian geometry. The geometrical objects are defined using the local coordinates. Moreover, algebra is used. In both two- and three-dimensional geometry, analytical geometry is useful. Basically, Analytic Geometry is the bridge between algebra and geometry where one equation written in algebra can represent a curve on cartesian coordinates using the analytic geometry.

Coordinate Plane

The planar space is divided into two dimensions by a coordinate plane, which is helpful for pinpointing the points. It is commonly called the cartesian plane. The two axes of the coordinate plane are the vertical y-axis and the horizontal x-axis. The origin(0,0) is the place where these coordinate axes connect, and they divide the plane into four quadrants. Additionally, any point in the coordinate plane is denoted by the coordinates (x, y), where x represents the point's position with respect to the x-axis and y represents its position with respect to the y-axis. To the right of the origin, the x-axis is positive, while to the left of the origin, the x-axis is negative. Similarly, the y-axis above the origin is positive while that below the origin is negative.

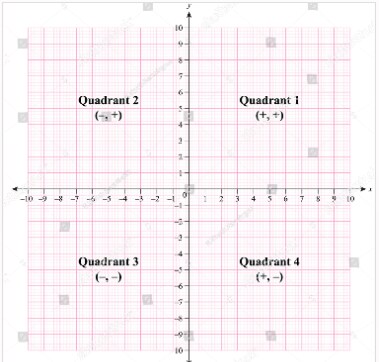
Quadrants

The two coordinate axes, namely the x-axis, and y-axis divide the coordinate plane into four quadrants.

• A point (x, y) plotted with reference to the positive x-axis and the positive y-axis has both positive values and is located in the first quadrant.

• A point (-x, y) plotted with reference to the negative x-axis and the positive y-axis is located in the second quadrant.

• A point (-x, -y) plotted with reference to the negative x-axis and the negative y-axis has both negative values and is located in the third quadrant.

• A point (x, -y) plotted with reference to the positive x-axis and the negative y-axis is located in the fourth quadrant.

https://www.shutterstock.com/image-vector/maths-graph-pink-grid-4-quadrant-1539462425

Coordinates Of A Point

In the Cartesian coordinate system, each point has an x-coordinate and a y-coordinate describing its horizontal location and vertical position, respectively. Typically, they are referred to as an ordered pair and marked as (x, y). This system is also applicable to three-dimensional geometry, in which each point is represented by an ordered triple of coordinates (x, y, z) in Euclidean space.

The abscissa is defined as the value of x for the point (x, y), where x is the distance from the origin along the x-axis. The ordinate is defined as the value of y for the point (x, y), where x is the perpendicular distance from the x-axis.

Types Of Coordinates

Analytical geometry uses a variety of coordinate types. Here are a few examples:

• Cartesian coordinates

In this case, each point has an x-coordinate and y-coordinate that express their relative horizontal and vertical positions. Typically, they are referred to as an ordered pair and marked as (x, y).

• Polar coordinates

In this case, the distance “r” from the origin and the angle from the polar axis are used to represent each point in a plane.

• Cylindrical coordinates

In this case, the height, radius from the z-axis, and angle projected on the xy- plane with regard to the horizontal axis of each point act as a representation of that point.

• Spherical coordinates

In this case, the distance from the origin, the angle projected on the xy plane with regard to the horizontal axis, and another angle with respect to the z-axis all help to determine a point in space.

Analytic Geometry Formulas

• Distance Formula

For two points A and B, having the coordinates (a,b) and (c,d), the distance(d) between the two points is calculated by calculating the squares of the x- and y-coordinates of the two given points' differences.

d=\sqrt{(c-a)^{2}+(d-b)^{2}

• Midpoint Theorem Formula

For two points A and B, having the coordinates (a,b) and (c,d), the coordinates of the midpoint(M) of the line connecting the two points are computed by finding the abscissa which is the average of the x values of the two given points, and the ordinate which is the average of the y values of the two given points.

Coordinates of M = (\frac{a+c}{2},\frac{b+d}{2})

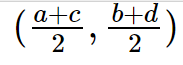
• Angle Formula

For two lines having slopes m and n respectively, and the angle between them is a, then,

\tan a=\frac{m-n}{1+mn}

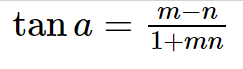
• Section Formula

Considering two points A and B having the coordinates (a,b) and (c,d) respectively. The coordinates of point P if it divides the line AB in the ratio m:n are given as:

(\frac{mb+na}{m+n},\frac{md+nc}{m+n})

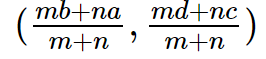
Analytic Geometry In Three Dimensions

In this scenario, we take into consideration triplets (a, b, c), which are real numbers. We refer to this set as a three-dimensional number space and abbreviate it R3. The triplets' constituents are all referred to as coordinates. We take into account three mutually perpendicular lines intersecting at point O in three-dimensional space. The point O is referred to as origin and the three perpendicular lines are referred to as axes.