Area Of A Circle - GCSE Maths - Steps, Examples & Worksheet

Area Of Circle Questions

Edited By Team Careers360 | Updated on Jul 02, 2025 05:27 PM IST

The area of a circle is the area that a circle occupies on a two-dimensional plane. Alternately, the area of the circle is the area enclosed inside the circumference or perimeter of the circle. For measuring the area occupied by a circular field or plot, use the area of a circle formula. The area formula will also enable us to determine the circle's circumference or boundary length. There is no volume in a circle. A circle has only two dimensions and has no volume. Only the area and circumference or perimeter of a circle are defined.

This Story also Contains

What Is A Circle?
Parts Of A Circle
What Is The Area Of A Circle?
Formulas For Calculating The Area Of A Circle
Formulas To Remember

What Is A Circle?

A circle is made up of a group of points that are spaced uniformly apart from its centre. A circle is a locus of a point moving around a fixed point at a defined distance from the point in mathematical terms. The circle's radius is its constant distance from the centre.

Parts Of A Circle

Radius - The radius of a circle is the distance from the centre to a point on the periphery. It is symbolised by the letter ‘r’ or ‘R’.
Diameter - The diameter of a circle is defined as the length of a line with its ends on the circle and passing through its centre. It is symbolised by the letter ‘d’ or ‘D’. The line dividing a circle into two equal parts is known as the diameter of the circle. We might state that the diameter is merely the circle's radius multiplied by two, this means that, D=2R. We can determine the radius of the circle if we know its diameter, for example; R=D/2.
Circumference - The length of a circle's boundary determines its circumference. This implies that a circle's circumference and perimeter are equal. The following formula can be used to get the circumference:

Circumference= 2\pi R 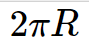1707112185134 , and as R=D/2, additionally, circumference may be computed as: 2\pi (D/2)=\pi D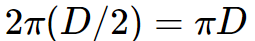 1707112185644

What Is The Area Of A Circle?

The measure of space enclosed within a circle's periphery is known as its area. The area that the circle occupies is that which lies within its circumference. It is also known as the total number of square units contained within that circle. The area of a circle is therefore the area that is covered by one full cycle of its radius on a two-dimensional plane.

Formulas For Calculating The Area Of A Circle

For a circle with a radius ‘R’, the radius squared and the product of pi determine the area of this circle(A). It is calculated as:

A=\pi R^{2}

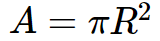
1707112185548

The unit of area is square units. Here, the value of pi is 22/7 or 3.14

Formulas To Remember

If the radius is known, the area of the circle is calculated as A=\pi R^{2}

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

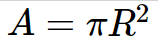
1707112184981

When the diameter is known, the area of a circle is calculated as A=\pi d^{2}/4

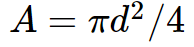
1707112185291

When the circumference is known, the area of a circle is calculated as A=C^{2}/4\pi

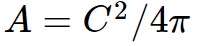
1707112185714

Frequently Asked Questions (FAQs)

1. Define the area of a circle.

The space a circle takes up in a two-dimensional plane is known as the area of the circle. The area of the circle is the area enclosed inside the circumference or perimeter of the circle.

2. Does a circle have volume?

There is no volume in a circle. A circle has only two dimensions and has no volume. Only the area and circumference or perimeter of a circle are defined.

3. Define a circle.

A circle is made up of a group of points that are spaced uniformly apart from its centre. A circle is a locus of a point that is moving at a fixed radius from a fixed point.

4. What is a circle's diameter and how does it relate to the radius?

The diameter of a circle is defined as the length of a line with its ends on the circle and passing through its centre. It is symbolised by the letter ‘d’ or ‘D’. The line dividing a circle into two equal parts is known as the diameter of the circle. We can determine the radius of the circle if we know its diameter, for example; R=D/2.

5. How does the concept of limits relate to the area of a circle?

The concept of limits is fundamental to understanding the area of a circle. Historically, mathematicians approximated the circle's area by inscribing polygons with increasing numbers of sides. As the number of sides approaches infinity, the area of the polygon approaches the true area of the circle. This limit concept forms the basis for the derivation of the circle area formula.

6. Can the area of a circle ever be a whole number?

While it's possible for the area of a circle to be very close to a whole number, it's extremely rare for it to be exactly a whole number due to the irrational nature of π. The area will almost always be an irrational number. However, in practical applications, we often round to a certain number of decimal places.

7. How does changing the radius affect the area of a circle?

Changing the radius has a significant impact on the area of a circle due to the squared relationship. If you double the radius, the area increases by a factor of 4. If you triple the radius, the area increases by a factor of 9. This non-linear relationship is why small changes in radius can lead to large changes in area.

8. Why is π (pi) used in the formula for circle area?

π (pi) is used in the formula for circle area because it represents the ratio of a circle's circumference to its diameter. This constant relationship exists for all circles, regardless of size. π appears in the area formula because the area is derived from the relationship between the circumference and radius.

9. How do you calculate the area of a semicircle?

To calculate the area of a semicircle, you first find the area of the full circle using A = πr², then divide this result by 2. The formula for a semicircle's area is therefore A = (πr²)/2 or A = ½πr². Remember, r is the radius of the full circle, not the length of the semicircle's curved edge.

10. What is the formula for the area of a circle?

The formula for the area of a circle is A = πr², where A is the area, π (pi) is approximately 3.14159, and r is the radius of the circle. This formula represents the relationship between the circle's radius and its area.

11. Why is the area of a circle proportional to the square of its radius?

The area of a circle is proportional to the square of its radius because as the radius increases, the circle grows in two dimensions simultaneously. This quadratic relationship is reflected in the r² term in the formula A = πr². It means that doubling the radius will increase the area by a factor of four.

12. What's the difference between diameter and radius in calculating circle area?

The diameter is twice the length of the radius. When calculating the area of a circle, we use the radius in the formula A = πr². If you're given the diameter, you need to divide it by 2 to get the radius before using the formula. Alternatively, you can use the formula A = π(d/2)², where d is the diameter.

13. How do you find the radius of a circle if you know its area?

To find the radius of a circle when you know its area, you need to use the inverse of the area formula. Start with A = πr², then solve for r: r = √(A/π). This means you divide the area by π and then take the square root of the result to find the radius.

14. How is the area of a circle related to its circumference?

The area of a circle is related to its circumference through the radius. The circumference is C = 2πr, while the area is A = πr². If you know the circumference, you can find the radius (r = C/2π) and then use this to calculate the area. The area is equal to the radius multiplied by half the circumference: A = r * (C/2).

15. How do you find the area of a circular sector?

To find the area of a circular sector, you use the formula A = (θ/360°) * πr², where θ is the central angle in degrees and r is the radius. This formula represents the fraction of the full circle's area that the sector occupies. For example, a sector with a 90° angle would have 1/4 of the circle's total area.

16. How do you calculate the area of an ellipse, and how does it relate to circle area?

The area of an ellipse is calculated using the formula A = πab, where a and b are the lengths of the semi-major and semi-minor axes. This formula is a generalization of the circle area formula, where a = b = r. The relationship between ellipse and circle areas showcases how circular symmetry extends to more complex shapes. An ellipse can be thought of as a 'stretched' circle, and its area formula reflects this transformation.

17. How do you find the area of a circular ring (annulus)?

To find the area of a circular ring (annulus), you subtract the area of the smaller inner circle from the area of the larger outer circle. If R is the radius of the outer circle and r is the radius of the inner circle, the formula is: A = π(R² - r²). This formula works because the ring is the difference between two circular areas.

18. What's the difference between π and τ (tau) in circle calculations?

π (pi) and τ (tau) are both constants used in circle calculations, where τ = 2π. Some mathematicians argue that τ is more intuitive for understanding circles. With τ, the area formula becomes A = ½τr², which directly relates to the formula for the area of a triangle (½ * base * height). However, π remains the more commonly used constant in practice.

19. What's the relationship between the areas of concentric circles?

For concentric circles (circles with the same center but different radii), the area between any two circles is proportional to the difference of the squares of their radii. If you have circles with radii r₁, r₂, r₃, etc., the area between the first and second circle is π(r₂² - r₁²), between the second and third is π(r₃² - r₂²), and so on.

20. What's the relationship between the area of a circle and the area of a square with the same perimeter?

A circle always has a larger area than a square with the same perimeter. This is due to the circle's optimal shape for enclosing area. If a square and circle have the same perimeter, the ratio of the circle's area to the square's area is π/4, or approximately 0.7854. This demonstrates the circle's efficiency in maximizing area for a given perimeter.

21. What's the relationship between the golden ratio and circle area?

The golden ratio, approximately 1.618, doesn't directly relate to the area of a circle, but it does have an interesting connection. If you construct a rectangle where the ratio of its length to its width is the golden ratio, the area of this rectangle is equal to the area of a circle whose diameter is the same as the rectangle's width. This relationship showcases the aesthetic properties often attributed to both the golden ratio and circles.

22. How does altitude affect circle area calculations on Earth?

Altitude affects circle area calculations on Earth because the Earth is not a perfect sphere. As altitude increases, the curvature of the Earth becomes more pronounced, affecting the actual surface area covered by what appears to be a circle from above. For very large circles (like those used in geography), corrections must be made to account for the Earth's curvature. This is part of the field of geodesy, which deals with the Earth's geometric shape.

23. What's the difference between Euclidean and non-Euclidean geometry in terms of circle area?

In Euclidean geometry (flat space), the area of a circle is always πr². However, in non-Euclidean geometries, such as on a sphere (positive curvature) or a hyperbolic plane (negative curvature), this formula changes. On a sphere, the area of a circle is less than πr² and has a maximum possible value. On a hyperbolic plane, the area grows faster than πr². These differences highlight how the nature of space itself affects geometric properties.

24. How does the concept of circle area extend to higher dimensions?

The concept of circle area extends to higher dimensions through hyperspheres. In 3D, we have a sphere with volume V = 4/3πr³. In 4D, we have a hypersphere with hypervolume V = 1/2π²r⁴. This pattern continues into higher dimensions, with the general formula for an n-dimensional hypersphere's hypervolume involving π^(n/2) and r^n. These extensions help mathematicians and physicists understand and work with higher-dimensional spaces.

25. Why is the area of a circle maximum for a given perimeter?

A circle has the maximum area for a given perimeter because it's the most efficient shape for enclosing area. This property, known as the isoperimetric inequality, stems from the circle's perfect symmetry. Any deviation from a circular shape would create 'corners' that reduce the enclosed area while maintaining the same perimeter. This principle is why bubbles form spheres in three dimensions - to maximize volume for a given surface area.

26. How does the area of a circle change if you cut out a sector?

When you cut out a sector from a circle, the remaining area is called a circular segment. To find its area, you subtract the area of the sector from the full circle's area. The sector's area is given by (θ/360°) * πr², where θ is the central angle in degrees. So, the segment's area is πr² - (θ/360°) * πr².

27. Can you have a negative area for a circle?

No, you cannot have a negative area for a circle. Area is a measure of the amount of space enclosed within a boundary, and this is always a positive quantity or zero. Even if you're dealing with negative coordinates on a plane, the area itself will always be positive. A negative radius in the formula A = πr² would result in a positive area due to the square.

28. How does the concept of circle area apply in real-world scenarios?

The concept of circle area has numerous real-world applications. It's used in designing circular objects like wheels, plates, or manhole covers. In agriculture, it helps calculate the area covered by circular irrigation systems. In physics, it's crucial for understanding concepts like pressure (force per unit area). In construction, it's used for planning circular structures or calculating the amount of material needed for circular floors or ceilings.

29. Why doesn't doubling the radius of a circle double its area?

Doubling the radius of a circle doesn't double its area because of the squared relationship in the area formula (A = πr²). When you double the radius, you're actually quadrupling the area. This is because (2r)² = 4r². So, doubling the radius results in an area that's 4 times the original area, not 2 times.

30. How do you estimate the area of an irregular shape using circles?

To estimate the area of an irregular shape using circles, you can use a method called circle packing. This involves fitting as many circles of various sizes as possible within the shape, then summing their areas. Alternatively, you can use a single circle that approximates the shape's area, or divide the shape into sections that can be approximated by circular sectors or segments.

31. How is the area of a circle used in probability and statistics?

The area of a circle is crucial in probability and statistics, particularly in understanding normal distributions. The bell curve of a normal distribution is based on a circle's equation. In probability, the area under this curve represents the likelihood of events occurring. Circular areas are also used in creating pie charts, where the area of each sector represents the proportion of a particular category.

32. How does the concept of circle area apply in physics, particularly in fields like optics?

In physics, particularly in optics, the concept of circle area is fundamental. For example, the amount of light passing through a circular aperture is proportional to its area. This principle is crucial in camera design, telescope construction, and understanding the human eye. In wave optics, circular apertures produce diffraction patterns described by Bessel functions, where the area of the aperture determines the intensity distribution. The concept also applies in other areas like fluid dynamics and electromagnetism.

33. What's the relationship between circle area and the concept of pi in computer science?

In computer science, calculating the area of a circle often serves as an introduction to working with irrational numbers like pi. It highlights the need for approximation in digital systems, as pi cannot be exactly represented in finite memory. Algorithms for approximating pi, such as the Monte Carlo method, often involve calculating circle areas. Additionally, circular area calculations are used in computer graphics, game physics, and data visualization, demonstrating the practical applications of this mathematical concept in programming.

34. What's the connection between the area of a circle and the volume of a sphere?

The area of a circle and the volume of a sphere are closely related. The formula for the volume of a sphere (V = 4/3πr³) can be derived from the area of a circle. Imagine slicing a sphere into many thin circular disks. The volume of each disk is approximately its circular area times its thickness. Integrating these over the sphere's radius gives the volume formula, showing how 2D circular area extends to 3D spherical volume.

35. What role does dimensional analysis play in understanding circle area?

Dimensional analysis is crucial for understanding circle area. The area must have units of length squared (L²). In the formula A = πr², r has units of length (L), so r² has units L². The constant π is dimensionless, preserving the L² units. This analysis helps verify the correctness of area calculations and formulas, and it's a powerful tool for checking work and understanding the physical meaning of mathematical expressions involving areas.

36. What's the connection between circle area and the concept of pi day?

Pi Day, celebrated on March 14th (3/14 in month/day format), honors the mathematical constant π, which is crucial in calculating circle area. The day promotes mathematics education and appreciation, often featuring activities related to circles and pi. These might include calculating areas of various circular objects, demonstrating how pi is derived from circle measurements, or exploring the history of pi's calculation. It highlights the fundamental role of pi in understanding circles and their properties.

37. How does the area of a circle relate to calculus and integration?

The area of a circle is intimately connected to calculus and integration. In fact, one way to derive the area formula is through integration. If you consider a circle as made up of infinitesimally thin concentric rings, the area can be found by integrating these rings from the center to the edge. This process leads to the integral ∫2πr dr from 0 to R, which evaluates to πR². This approach demonstrates how calculus provides a deeper understanding of geometric concepts.

38. What's the significance of circle area in optimization problems?

Circle area plays a crucial role in many optimization problems. For instance, the classic problem of maximizing the area enclosed by a fixed perimeter is solved by a circle. In engineering, circular designs often optimize material use or strength. In city planning, circular layouts can minimize average travel distances. Understanding how area changes with radius helps in finding optimal solutions in fields ranging from antenna design to efficient packing problems.

39. How does the area of a circle relate to the concept of scaling in mathematics?

The area of a circle beautifully illustrates the concept of scaling in mathematics. When you scale a circle by a factor k (multiplying its radius by k), its area increases by a factor of k². This non-linear scaling is a key concept in understanding how properties change with size across various fields. It's why, for example, the surface area-to-volume ratio changes as objects get larger, affecting heat dissipation in biology and engineering. This scaling property of circles extends to other shapes and higher dimensions, forming a fundamental principle in geometry and applied mathematics.

40. What's the connection between circle area and the concept of radians?

Radians and circle area are closely related. One radian is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius. This definition creates a natural relationship between angle measure and area. The area of a sector with angle θ in radians is A = ½r²θ, which is simpler than the degree-based formula. This connection highlights why radians are often preferred in advanced mathematics and physics, as they relate more directly to the circle's geometry.

41. How does understanding circle area help in comprehending more complex geometric shapes?

Understanding circle area provides a foundation for comprehending more complex geometric shapes. Many shapes can be broken down into or approximated by circular components. For instance, the area of an ellipse is a direct modification of the circle formula. Circular sectors and segments are used to calculate areas of more complex curved shapes. In calculus, techniques used to derive the circle area formula (like integration) extend to finding areas of arbitrary shapes. This foundational knowledge aids in understanding everything from conic sections to multidimensional geometries.

42. What role does circle area play in understanding fractals?

Circle area plays an interesting role in understanding fractals, which are complex geometric shapes with self-similarity at different scales. Some fract