Conditional Probability: Definition, Formula, Properties and Examples

Probability is defined as the ratio of the number of favorable outcomes to the total number of outcomes. Conditional probability is an operation of set theory that helps to measure the probability of an event occurring when another event has already occurred. It provides a way to update probabilities based on new information and is essential for understanding how events interact and depend on each other. This event occurs very frequently in normal life and conditional probability is used to determine those cases.

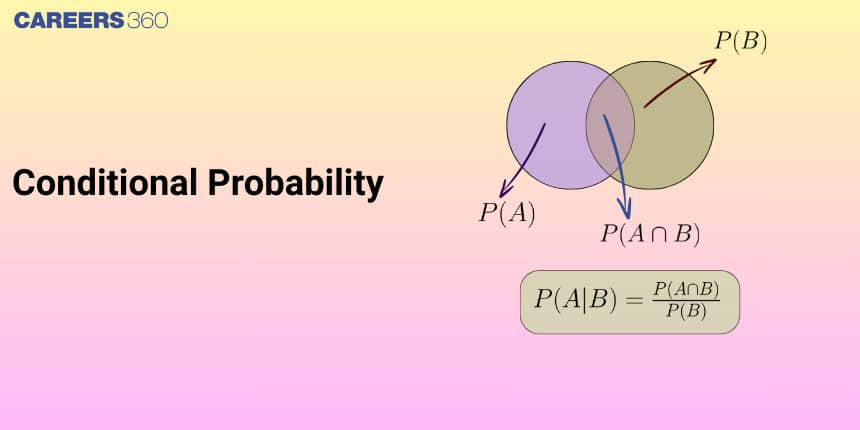
Conditional Probability

Conditional probability is a measure of the probability of an event given that another event has already occurred. If A and B are two events associated with the same sample space of a random experiment, the conditional probability of the event A given that B has already occurred is written as $P(A \mid B), P(A / B)$ or $P\left(\frac{\{A\}}{\{B\}}\right)$.

The formula to calculate $P(A \mid B)$ is
$P(A \mid B)=\frac{\{P(A \cap B)\}}{\{P(B)\}}$ where $P(B)$ is greater than zero.
For example, suppose we toss one fair, six-sided die. The sample space $S=\\{1,2,3, 4,5,6\\}$. Let $A=$ face is $2$ or $3$ and $B=$ face is even number $(2,4,6)$.

Here, $P(A|B)$ means the probability of occurrence of face $2$ or $3$ when an even number has occurred which means that one of $2, 4$ and $6$ has occurred.

To calculate $P(A|B),$ we count the number of outcomes $2$ or $3$ in the modified sample space $B = \{2, 4, 6\}:$ meaning the common part in $A$ and $B$. Then we divide that by the number of outcomes in $B$ (rather than $S$).

$\begin{aligned} P(A \mid B) & =\frac{P(A \cap B)}{P(B)}=\frac{\frac{n(A \cap B)}{n(S)}}{\frac{n(B)}{n(S)}} \\ & =\frac{\frac{\text { the number of outcomes that are } 2 \text { or } 3 \text { and even in } S)}{6}}{\frac{\text { (the number of outcomes that are even in } S)}{6}} \\ & =\frac{\frac{1}{6}}{\frac{3}{6}}=\frac{1}{3}\end{aligned}$

Properties of Conditional Probability

Let $A$ and $B$ are events of a sample space $S$ of an experiment, then

Property $1: \mathrm{P}(\mathrm{S} \mid \mathrm{A})=\mathrm{P}(\mathrm{A} \mid \mathrm{A})=1$
Proof:

Also,

$
\begin{aligned}
& P(S \mid A)=\frac{P(S \cap A)}{P(A)}=\frac{P(A)}{P(A)}=1 \\
& P(A \mid A)=\frac{P(A \cap A)}{P(A)}=\frac{P(A)}{P(A)}=1
\end{aligned}
$
Thus,

$
\mathrm{P}(\mathrm{S} \mid \mathrm{A})=\mathrm{P}(\mathrm{A} \mid \mathrm{A})=1
$

Property 2 If $A$ and $B$ are any two events of a sample space $S$ and $C$ is an event of $S$ such that $P(C) ≠ 0,$ then
$
P((A \cup B) \mid C)=P(A \mid C)+P(B \mid C)-P((A \cap B) \mid C)
$

In particular, if $A$ and $B$ are disjoint events, then

$
P((A \cup B) \mid C)=P(A \mid C)+P(B \mid C)
$

Proof:

$
\begin{aligned}
\mathrm{P}((\mathrm{A} \cup \mathrm{B}) \mid \mathrm{C}) & =\frac{\mathrm{P}[(\mathrm{A} \cup \mathrm{B}) \cap \mathrm{C}]}{\mathrm{P}(\mathrm{C})} \\
& =\frac{\mathrm{P}[(\mathrm{A} \cap \mathrm{C}) \cup(\mathrm{B} \cap \mathrm{C})]}{\mathrm{P}(\mathrm{C})}
\end{aligned}
$

(by distributive law of union of sets over intersection)

$
\begin{aligned}
& =\frac{P(A \cap C)+P(B \cap C)-P((A \cap B) \cap C)}{P(C)} \\
& =\frac{P(A \cap C)}{P(C)}+\frac{P(B \cap C)}{P(C)}-\frac{P[(A \cap B) \cap C]}{P(C)} \\
& =P(A \mid C)+P(B \mid C)-P((A \cap B) \mid C)
\end{aligned}
$

When $A$ and $B$ are disjoint events, then

$
\begin{aligned}
& \mathrm{P}((\mathrm{A} \cap \mathrm{B}) \mid \mathrm{C})=0 \\
& \Rightarrow \quad \mathrm{P}((\mathrm{A} \cup \mathrm{B}) \mid \mathrm{F})=\mathrm{P}(\mathrm{A} \mid \mathrm{F})+\mathrm{P}(\mathrm{B} \mid \mathrm{F})
\end{aligned}
$

Property $3: P\left(A^{\prime} \mid B\right)=1-P(A \mid B)$, if $P(B) \neq 0$
Proof:
From Property 1, we know that $\mathrm{P}(\mathrm{S} \mid \mathrm{B})=1$

$
\begin{array}{lll}
\Rightarrow & P\left(\left(A \cup A^{\prime}\right) \mid B\right)=1 & \left(\text { as } A \cup A^{\prime}=S\right) \\
\Rightarrow & P(A \mid B)+P\left(A^{\prime} \mid B\right)=1 & \text { (as } A \text { and } A^{\prime} \text { are disjoint } \\
\text { event) } & & \\
\Rightarrow & P\left(A^{\prime} \mid B\right)=1-P(A \mid B) &
\end{array}
$

Recommended Video Based on Conditional Probability

Solved Examples Based on Conditional Probability:

Example 1: One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that the Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is:

1) $\frac{1}{2}$
2) $\frac{1}{3}$
3) $\frac{2}{5}$
4) $\frac{1}{5}$

Solution

Conditional Probability
Let A and B be any two events such that $B \neq \phi$ or $\mathrm{n}(\mathrm{B})=0$ or $\mathrm{P}(\mathrm{B})=0$ then $P\left(\frac{A}{B}\right)$ denotes the conditional probability of occurrence of event $A$ when $B$ has already occurred

$
P\left(\frac{l_M l_W}{A_M A_W}\right)=\frac{4!\cdot(2!)^5}{5!\cdot(2!)^4}=\frac{2}{5}
$
Hence, the answer is option 3.

Example 2: In a random experiment, a fair die is rolled until two fours are obtained in succession. The probability that the experiment will end in the fifth throw of the die is equal to:
1) $\frac{200}{6^5}$
2) $\frac{150}{6^5}$
3) $\frac{225}{6^5}$
4) $\frac{175}{6^5}$

Solution

Probability of occurrence of an event -

Let $S$ be the sample space then the probability of occurrence of an event $E$ is denoted by $P(E)$ and it is defined as

$
\begin{aligned}
& P(E)=\frac{n(E)}{n(S)} \\
& P(E) \leq 1 \\
& P(E)=\lim _{n \rightarrow \infty}\left(\frac{r}{n}\right)
\end{aligned}
$
Where n repeated experiment and E occurs r times.
Conditional Probability -
Let A and B be any two events such that $B \neq \phi$ or $\mathrm{n}(\mathrm{B})=0$ or $\mathrm{P}(\mathrm{B})=0$ then $P\left(\frac{A}{B}\right)$ denotes the conditional probability of occurrence of event $A$ when $B$ has already occurred

$
\begin{aligned}
P(---4) & =P(4--44)+P(\text { not } 4--44) \\
& =\frac{1}{6} \times \frac{5}{6} \times \frac{5}{6} \times \frac{1}{6} \times \frac{1}{6}+\frac{5}{6} \times 1 \times \frac{5}{6} \times \frac{1}{6} \times \frac{1}{6} \\
& =\frac{25}{6^5}+\frac{25}{6^4} \\
& =\frac{175}{6^5}
\end{aligned}
$

Hence, the answer is the option 4.

Example 3: Three numbers are chosen at random without replacement from $\{1,2,3, \ldots \ldots .81\}$. The probability that their minimum is 3 , given that their maximum is 6 , is
1) $\frac{3}{8}$
2) $\frac{1}{5}$
3) $\frac{1}{4}$
4) $\frac{2}{5}$

Solution

Conditional Probability -

$
P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}
$
and
$
P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)}
$
where the probability of A when B already happened.
$A$ is the event that the maximum is 6 .
$B$ is the event that the minimum is 3 .

$
P(B / A)=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1 \cdot 1 \cdot 2}{8^8 C_3}}{\frac{{ }^5 C_2}{{ }^8 C_3}}=\frac{2}{10}=\frac{1}{5}
$

Example 4: It is given that the events $A$ and $B$ are such that $P(A)=\frac{1}{4}, P(A \mid B)=\frac{1}{2}$ and $P(B \mid A)=\frac{2}{3}$. Then $P(B)$ is:
1) $\frac{1}{2}$
2) $\frac{1}{6}$
3) $\frac{1}{3}$
4) $\frac{2}{3}$

Solution

Conditional Probability -

$
P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}
$

and

$
P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)}
$

where $P\left(\frac{A}{B}\right)$ probability of A when B already happened.

$
\begin{aligned}
& P(B \mid A) P(A)=P(A \mid B) P(B)=\stackrel{\text { 䂇 }}{P}(A \cap B) \\
& \Rightarrow \frac{1}{4} \times \frac{2}{3}=\frac{1}{2} \times P(B) \\
& \Rightarrow P(B)=\frac{1}{3}
\end{aligned}
$
Hence, the answer is the option 3.

Example 5: If C and D are two events such that $C \subset D$ and $P(D) \neq 0$, then the correct statement among the following is:
1) $P(C / D)<P(C)$
2) $P(C / D)=\frac{P(D)}{P(C)}$
3) $P(C / D)=P(C)$
4) $P(C / D) \geqslant P(C)$

Solution
Conditional Probability -
$
P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}
$
and
$
P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)}
$

where the probability of $A$ when $B$ already happened.

$
P\left(\frac{C}{D}\right)=\frac{P(C \cap D)}{P(D)}
$
If C and d are independent events
$
\begin{aligned}
& P(C \cap D)=P(C) \cdot P(D) \\
& \text { otherwise if } C \subseteq D \\
& P(C \cap D)=P(C) \\
& \therefore P\left(\frac{C}{D}\right)=\frac{P(C)}{P(D)} \geqslant P(C)
\end{aligned}
$
Hence, the answer is the option 4.

Summary
Conditional probability is a measure of the probability of an event given that another event has already occurred. Conditional Probability is a powerful tool in probability theory that helps in analyzing events based on new events. By mastering these concepts, complex problems can be solved effectively. This concept is crucial in various fields such as statistics and finance etc.