Probability: Definition, Theorems, and Applications
Imagine tossing a coin before a cricket match to decide who will bat first—that simple act is actually based on probability. In mathematics, probability helps us measure the chance of an event happening, whether it’s predicting exam results, ticket confirmation probability, or understanding real-world data through probability distribution functions. From basic concepts of probability to advanced topics like the conditional probability formula, this concept plays a major role in Class 11 and Class 12 maths, as well as competitive exams like JEE. By learning different probability formulas, rules, and applications, students can solve questions involving permutations, combinations, and even non-probability sampling techniques. In this article, we will explore probability theory in mathematics, important formulas, and examples that make the topic easy to understand.
What is Probability?
Probability is a measure of how likely an event is to happen. With the help of probability, we can predict the chance of an event to occur. The value of probability ranges between $0$ to $1$, where $0$ represents the impossible event and $1$ represents the probability of events that are certain to happen. Now,Let us look into the basic concepts of probability.
Types of Probability
- Classical Probability: Classical probability is based on the assumption that all outcomes of a random experiment are equally likely. It is calculated as the ratio of the number of favourable outcomes to the total number of possible outcomes. For example, the probability of rolling a $3$ on a fair six-sided die is $\frac{1}{6}$.
- Empirical Probability: Empirical probability is based on observed data rather than theoretical calculations. It is determined by conducting experiments or collecting data and then calculating the probability based on the relative frequency of an event occurring in the data. For example, if a coin is flipped 100 times and lands on heads $55$ times, the empirical probability of landing on heads is $\frac{55}{100}$ = $0.55$.
- Subjective Probability: Subjective probability is based on personal judgment, intuition, or experience rather than objective data or mathematical calculation. It reflects an individual's belief about the likelihood of an event occurring, which may vary from person to person. For example, someone might estimate a $70%$ chance of their favourite sports team winning a game based on their analysis and feelings about the team's performance.
- Axiomatic Probability: Axiomatic probability is a formal framework for probability theory based on a set of axioms or fundamental principles. It provides a rigorous foundation by defining probability functions and operations through axioms, such as the probability of the entire sample space being $1$ and the additivity of mutually exclusive events.
Probability Class 11 Terminolgies
Sample Space: The set of all possible outcomes in a random experiment is called a sample space. For example, the sample space for a coin toss is {Heads, Tails}.
- Outcome and Trial: A trial means doing or performing an experiment, and an outcome is the result of that experiment. For example, if rolling a dice is a trial, then getting a $3$ is an outcome.
- Event: An event is one of the specific outcomes of an experiment; in other words, an event is a subset of the sample space.
- Favourable Event: Favourable events are those events associated with the experiment which are of interest to us. When rolling a dice, if we are interested in even numbers, then getting a $2$ is called a favourable event.
- Non-favourable Event: Non-favourable events are those events associated with the experiment in which we are not interested. When rolling a die, if we are interested in even numbers, then getting a $3$ is called a non-favourable event.
- Exhaustive Events: Exhaustive events are all those events that take up all the possible outcomes of an experiment. When rolling a die, the exhaustive events are getting a $1, 2, 3, 4, 5,$ and $6$
- Mutually Exclusive Events: When some events can not happen at the same time or simultaneously, then they are called mutually exclusive events. When tossing a coin, getting a head or a tail are mutually exclusive event.
- Independent Events: Independent events are those events where the occurrence of one event does not affect the other event's occurrence or vice versa. For example, flipping a coin and rolling a die can be considered independent events.
- Impossible Events: An impossible event is an event which cannot happen. For example, rolling a $7$ on a standard six-sided die is an impossible event.
Probability of an Impossible Event
The probability of an impossible event is always $0$, as it can not happen under any situation. If you roll a standard six-sided die, it is impossible to get a $7$, as there is no $7$ on the die. So in this case, the probability of rolling a $7$ is $0$.
Probability of a sure event
The probability of a sure event is always 1 because it is certain to occur. When we flip a coin, we are certain to get a head or a tail, so getting a head or a tail in this case is a sure event. Hence, the probability of getting either heads or tails is 1, when we toss a coin.
Probability Class 12 Terminologies
Random Variable
A random variable is a real-valued function whose domain is the sample space of a random experiment.
Probability Distribution of a Random Variable
The probability distribution for a random variable describes how the probabilities are distributed over the values of the random variable.
The probability distribution of a random variable $X$ is the system of numbers
$
\begin{array}{rlllllll}
X & : & x_1 & x_2 & x_3 & \ldots & \ldots & x_n \\
P(X) & : & p_1 & p_2 & p_3 & \ldots & \ldots & p_n \\
& p_i \neq 0, & \sum_{i=1}^n p_i=1, & i=1,2,3, \ldots n
\end{array}
$
The real numbers $\underline{\underline{x_1},}, x_2, \ldots, x_n$ are the possible values of the random variable $X$ and $p_i(i=1,2, \ldots, n)$ is the probability of the random variable $X$ taking the value $x i$ i.e., $P\left(X=x_i\right)=p_i$
Types Of Probability Distribution:
1. Binomial distribution
2. Normal Distribution
3. Cumulative distribution frequency
Probability Concepts and Formulas
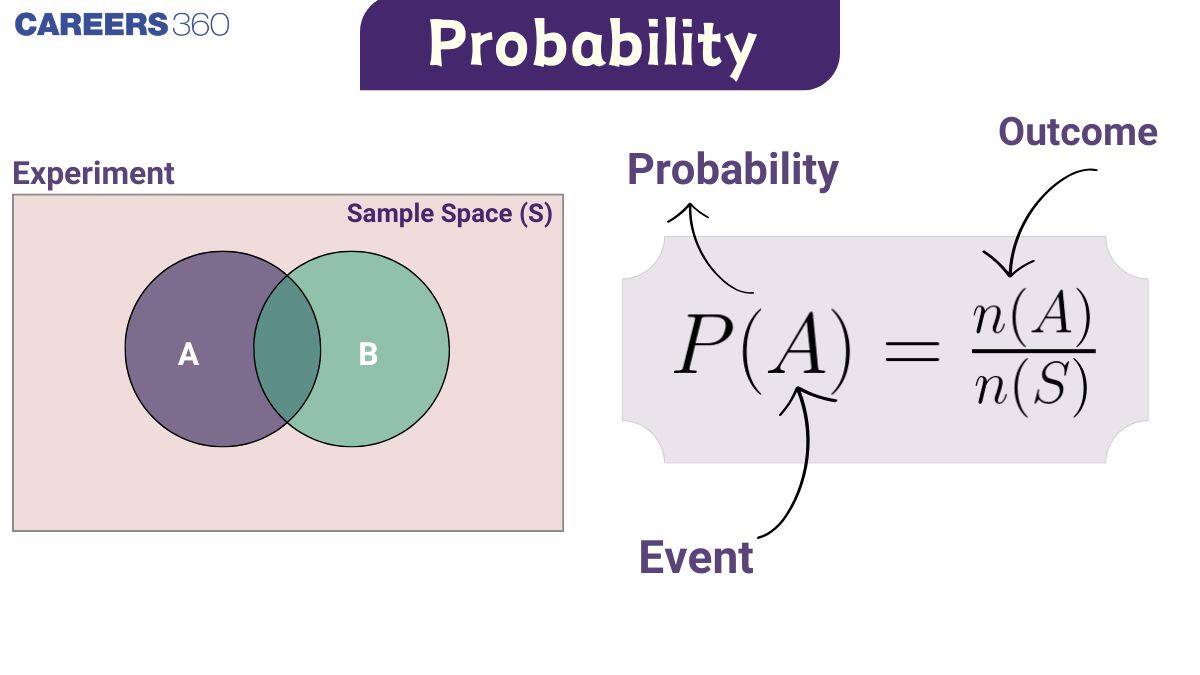
The probability of an event $A$ is written as $P(A)$, and it can easily calculated using the formula: $P(A) =\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
For example, while rolling a dice probability of getting a $6$ is $\frac{1}{6}$.
Steps to Calculate Probability
- Define the Experiment: Determine the process or action that generates outcomes.
- Identify the Sample Space: List all possible outcomes of the experiment.
- Determine the Favorable Outcomes: Identify which of these outcomes meet the criteria of the event of interest.
- Apply the Probability Formula: Use the formula to calculate the probability of the event.
Example: What is the probability of getting a number greater than $4$ when rolling a dice?
The experiment is rolling a single die.
The sample space $S$ consists of all possible outcomes: $S={1,2,3,4,5,6}$
The favourable outcomes are ${5,6}$
The required probability $= \frac{2}{6} = \frac{1}{3}$.
Probability of either of the two events occurring (Addition Rule)
The probability when either of two events occurs, or the addition rule, states that the probability of either of the two events occurring is the sum of their individual probabilities minus the probability of both events happening. The formula is:
$P(A \cup B) = P(A) + P(B) - P (A \cap B)$
Where $P(A \cup B)$ is the probability of either event $A$ or event $B$ occurring.
$P(A∩B)$ is the probability of both events $A$ and $B$ occurring.
$P(A)$ is the probability of event $A$ occurring.
$P(B)$ is the probability of event $B$ occurring.
Probability of a Complementary Event
Complementary events in probability are two such events which are mutually exclusive events which means they can not happen together. In other words, if one event occurs, then the other event can not occur. The sum of the probabilities of two complementary events is $1$. The formula:
$P(A′) = 1 - P(A)$
where $P(A)$ is the probability of the event $A$, and $P(A′)$ is the probability of the event $A′ $ (the complement of $A$).
Conditional Probability (Probability of $B$ if $A$ has already occurred)
Conditional probability is the probability of an event $B$ occurring given that another event $A$ has already happened. It is denoted by $P(B∣A)$. Conditional probability formula is
$P(B∣A) = \frac{P(A \cap B)}{P(A)}$
Where $P(B∣A)$ is the probability of event $B$ given that $A$ has occurred.
$P(A∩B)$ is the probability of both events $A$ and $B$ occurring.
$P(A)$ is the probability of event $A$ occurring.
Probability when two events occurred simultaneously
The probability of two events occurring simultaneously has two cases, one is when the events are independent and the other one is when the events are dependent.
- For independent events: If events $A$ and $B$ are independent, the probability of both events occurring simultaneously is the product of the probability of the individual events, it is given by: $P(A∩B) = P(A) × P(B)$
- For dependent events: When events $A$ and $B$ are dependent, the probability of both events occurring simultaneously is given by: $P(A∩B) = P(A) × P(B∣A)$, where $P(B∣A)$ is the conditional probability of event $B$ given that event $A$ has already occurred.
Theorems on Probability
Theorems on probability include Bayes' Theorem, Law of total probability, and some other theorems on probability.
Theorems on Probability Class 11
Theorem 1: The sum of the probability of happening of an event and not happening of an event is equal to $1$. $P(A) + P(A') = 1$.
Theorem 2: The probability of an impossible event or the probability of an event not happening is always equal to $0$. $P(ϕ) = 0$.
Theorem 3: The probability of a sure event is always equal to $1$. $P(A) = 1$
Theorem 4: The probability of happening of any event always lies between $0$ and $1$, i.e. $0 \leq P(A) \leq 1$.
Theorems on Probability Class 12
Theorem 1: If there are two events $A$ and $B$, we can apply the formula of the union of two sets and we can derive the formula for the probability of happening of event $A$ or event $B$ as follows.
$P(A∪B) = P(A) + P(B) - P(A∩B)$
Also for two mutually exclusive events $A$ and $B$, we have $P( A U B) = P(A) + P(B)$
Bayes’ Theorem for Conditional Probability
Bayes’ Theorem provides a way to update the probability of an event based on new evidence. It is expressed as $P(A∣B) = \frac{P(B∣A). P(A)}{P(B)}$
where $P(A∣B)$ is the probability of event $A$ given that event $B$ has occurred, $P(B∣A)$ is the probability of observing $B$ given $A$, $P(A)$ is the prior probability of $A$, and $P(B)$ is the total probability of $B$
Law of Total Probability
The Law of Total Probability states that the probability of an event can be found by considering all possible ways that event can occur through a partition of the sample space. It is expressed as $P(B) = \sum_{i} P(B|A_i). P(A_i)$, where $A_i$ are mutually exclusive and exhaustive events that partition the sample space. This law allows us to compute $P(B)$ by summing the probabilities of B occurring with each $A_i$ weighted by the probability of $A_i$.
Important Points
- The probability ranges from $0$ to $1$.
- The sum of probabilities of all possible outcomes in a sample space is $1$.
- For mutually exclusive events, the probability of either event occurring is the sum of their individual probabilities.
Probability tree
A probability tree is a diagram that represents all possible outcomes of an event and their probabilities. It is useful for calculating the probabilities of combined events.
Application of probability
Probability has a wide variety of applications in real life. Some of the common applications that we see in our everyday lives while checking the results of the following events:
- Choosing a card from the deck of cards
- Flipping a coin
- Throwing a dice in the air
- Pulling a red ball out of a bucket of red and white balls
- Winning a lucky draw
Understanding the deck of cards
A standard deck has $52$ cards with $4$ suits in two colors [hearts, diamonds, clubs, spades] each containing $13$ ranks $(2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace)$.
Tossing of a coin, Tossing of two or more coins
Each coin toss has $2$ possible outcomes. Tossing two coins can result in $HH, HT, TH,$ or $TT$.
Rolling a dice
A standard die has $6$ faces numbered $1$ to $6$. Each face has an equal probability of $\frac{1}{6}$.
Important Formulae for Probability
We have provided below the important formulae, along with the key note that specifies why is it used. With these important formulae, you will get to know how to use them while solving different problems.
| Concept / Rule | Formula | Key Note |
|---|---|---|
| Probability (equally likely finite outcomes) | $P(E)=\dfrac{n(E)}{n(S)}$ | $n(E)$ = favourable outcomes, $n(S)$ = total outcomes (use when outcomes are equally likely). |
| Basic properties | $0 \le P(E) \le 1,\quad P(S)=1,\quad P(\varnothing)=0$ | Range and certainty/extremes. |
| Complement | $P(E^c)=1-P(E)$ | Probability that event $E$ does not occur. |
| Addition rule (two events, general) | $P(A\cup B)=P(A)+P(B)-P(A\cap B)$ | Removes double counting of the intersection. |
| Addition rule (n events) — inclusion–exclusion | $P\Big(\bigcup_{i=1}^n A_i\Big)=\sum_i P(A_i)-\sum_{i<j}P(A_i\cap A_j)+\sum_{i<j<k}P(A_i\cap A_j\cap A_k)-\cdots$ | General formula for unions of many events. |
| Mutually exclusive events | $A_i\cap A_j=\varnothing\ (i\ne j)\Rightarrow P\Big(\bigcup_{i=1}^n A_i\Big)=\sum_{i=1}^n P(A_i)$ | Use when events cannot happen together. |
| Conditional probability | $P(A\mid B)=\dfrac{P(A\cap B)}{P(B)},\quad P(B)>0$ | Probability of $A$ given $B$ has occurred. |
| Multiplication rule (general) | $P(A\cap B)=P(A),P(B\mid A)=P(B),P(A\mid B)$ | Useful for sequential events and dependent events. |
| Independence (two events) | $A\perp B \iff P(A\cap B)=P(A)P(B)\iff P(A\mid B)=P(A)$ | If independent, knowledge of one does not change the other. |
| Total probability theorem (partition) | $P(B)=\sum_{i} P(A_i),P(B\mid A_i)$ | ${A_i}$ is a partition of the sample space. |
| Bayes’ theorem | $P(A_k\mid B)=\dfrac{P(A_k),P(B\mid A_k)}{\sum_i P(A_i),P(B\mid A_i)}$ | Converts $P(B\mid A)$ into $P(A\mid B)$ using a partition. |
| “At least one” (complement trick) | $P(\text{at least one success})=1-P(\text{no successes})$ | Often used in repeated trials to avoid summing many cases. |
| Binomial distribution (PMF) | $P(X=k)={n\choose k},p^{k},(1-p)^{,n-k},\quad k=0,\dots,n$ | $n$ independent trials, success probability $p$. |
| Hypergeometric distribution | $P(X=k)=\dfrac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}}$ | Sampling without replacement: population size $N$, $K$ successes, sample $n$. |
| Geometric distribution (first success on $k$) | $P(X=k)=(1-p)^{,k-1}p,\quad k=1,2,\dots$ | Trials until first success (memoryless property). |
| Poisson distribution | $P(X=k)=\dfrac{e^{-\lambda}\lambda^{k}}{k!},\quad k=0,1,\dots$ | Models rare events; $\lambda$ = average rate. |
| Expectation (mean) — discrete & continuous | $E[X]=\sum_x x,P(X=x)\quad\text{or}\quad E[X]=\int_{-\infty}^{\infty} x,f(x),dx$ | Weighted average of outcomes. |
| Variance | $\operatorname{Var}(X)=E[X^2]-\big(E[X]\big)^2$ | Measure of spread. |
| Binomial mean & variance | $E[X]=np,\quad \operatorname{Var}(X)=np(1-p)$ | For $X\sim\mathrm{Binomial}(n,p)$. |
| Poisson mean & variance | $E[X]=\lambda,\quad \operatorname{Var}(X)=\lambda$ | For $X\sim\mathrm{Poisson}(\lambda)$. |
| CDF (cumulative) | $F_X(x)=P(X\le x)$ | For discrete or continuous random variables. |
| Permutations & combinations | $^nP_r=\dfrac{n!}{(n-r)!},\quad {n\choose r}=\dfrac{n!}{r!(n-r)!}$ | Counting tools used to compute $n(E)$ and $n(S)$ for probabilities. |
List of Topics related to probability according to NCERT/JEE MAIN
This section covers all the important topics in probability that are part of the Class 11 and Class 12 NCERT syllabus and frequently asked in JEE Main exams.
Important Books and Resources for Probability
Here you will find the best reference books and study materials that explain probability formulas, concepts, and problem-solving methods in detail.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Mathematics Class 12 | NCERT | Official textbook with detailed theory and exercises on probability. |
| Mathematics for Class 12 | R.D. Sharma | Comprehensive explanations and solved problems on probability concepts. |
| Objective Mathematics | R.S. Aggarwal | Topic-wise MCQs with practice questions for probability. |
| Arihant All-In-One Mathematics | Arihant | Exhaustive coverage including probability with sample papers. |
| Fundamentals of Probability | S. Ross | Strong theoretical base and problem sets for advanced learners. |
NCERT Resources
This section highlights key NCERT textbooks and chapters that build a strong foundation in probability for board exams and competitive exams.
NCERT Maths Solutions for Class 12th Chapter 13 - Probability
NCERT Maths Exemplar Solutions for Class 12th Chapter 13 - Probability
NCERT Subjectwise Resources
Here, we explore subject-wise NCERT resources such as notes, solutions, and exemplar solutions to help you prepare effectively.
| Subject | NCERT Notes Link | NCERT Solutions Link | NCERT Exemplar Link |
|---|---|---|---|
| Mathematics | NCERT notes Class 12 Maths | NCERT solutions for Class 12 Mathematics | NCERT exemplar Class 12 Maths |
| Physics | NCERT notes Class 12 Physics | NCERT solutions for Class 12 Physics | NCERT exemplar Class 12 Physics |
| Chemistry | NCERT notes Class 12 Chemistry | NCERT solutions for Class 12 Chemistry | NCERT exemplar Class 12 Chemistry |
Practice Questions based on Probability
This part includes a set of practice questions designed to strengthen your understanding of probability concepts and improve problem-solving speed.
Frequently Asked Questions (FAQs)
Probability is the measure of how likely an event is to happen. It is calculated as the ratio of favourable outcomes to total possible outcomes.
The probability of an event $E$ is given by
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$
The main types are:
Theoretical probability (based on reasoning)
Experimental probability (based on observations/experiments)
Conditional probability (depends on another event)
Joint probability (two events happening together)
A probability distribution shows how probabilities are assigned to different possible outcomes of a random variable. For example, in tossing a die, each outcome (1 to 6) has equal probability $1/6$.
The probability of an impossible event is $0$.
Conditional probability formula is $P(B∣A) = \frac{P(A \cap B)}{P(A)}$
Where $P(B∣A)$ is the probability of event $B$ given that $A$ has occurred.
$P(A∩B)$ is the probability of both events $A$ and $B$ occurring.
$P(A)$ is the probability of event $A$ occurring.
Questions related to
On Question asked by student community
There is a small chance that the cutoff might reduce in round 3 in Punjab for the SC category under the defense quota. The change depends on how many seats are left after round 2 and how many students with similar marks are still in the race.
If some seats remain empty or if a few candidates withdraw their admissions, the cutoff can drop a little. This sometimes happens in special quotas like SC or defense. But if the seats are already full or many students with similar scores are still waiting, the cutoff might stay the same.
Since your score is 367 and you are close to the round 2 cutoff, you have a fair chance if there is even a small drop in round 3. Still, it is not guaranteed because the drop is usually very small in the final rounds.
Hi dear candidate,
With the rank of 11272 in AP EAMCET you can get decent colleges under convenor seat in agriculture. The top colleges like Acharya N.G Ranga Agricultural University (ANGRAU) requires rank to be under 5,000 so, this might not be under your rank.
Colleges like JNTUK or VRSEC Vijayawada might be available for you.
For the best available colleges as per your rank, use our official college prediction tool:
AP EAMCET College Predictor 2025 - Predict Colleges based on your Rank
ALL THE BEST !
Hello Harsha,
It would be quite difficult to get CSE in the JNTU campuses (JNTU Kakinada, JNTU Anantapur, or JNTU Vizianagaram) with an AP EAPCET rank of 18,000 in the OC-EWS category (male) because the cutoff for CSE in JNTU's typically goes in the top 5,000–10,000 ranks.
Although it is not saying much, you might have a slim chance for lower demand branches like IT or ECE in JNTU Vizianagaram or JNTU Kalikiri depending on this year's seat matrix and the competition. AP ECET Rank vs college
hi,
11,320 in TS EAPCET and aiming for a veterinary seat, it is very difficult to get a seat in government veterinary colleges. Veterinary seats are highly competitive, and usually, the cutoffs for veterinary courses in Telangana close around 4,000 to 5,000 rank, especially for open and BC categories.
Hello Ankit,
With a NEET 2025 score of approximately 540–550 and belonging to the SC category, securing admission to AIIMS Kalyani for the MBBS program is highly unlikely.
AIIMS Kalyani NEET Cutoff for SC Category:
-
In 2024, the closing NEET score for SC candidates at AIIMS Kalyani was around 658.
-
In 2023, the closing NEET score for SC candidates at AIIMS Kalyani was approximately 613.
Given these trends, a score of 540–550 falls significantly below the previous years' cutoffs for the SC category at AIIMS Kalyani.
Alternative Options:
-
Consider applying to other medical colleges where the cutoff for SC candidates is lower.
-
Participate in both All India Quota (AIQ) and state-level counselling processes to maximize your chances of securing a seat.
-
Explore private medical colleges that may have lower cutoff scores and offer scholarships or financial aid for SC category students.
It's important to research and apply to multiple institutions to increase your chances of admission.
I hope this answer helps you. If you have more queries, feel free to share your questions with us, and we will be happy to assist you.
Thank you, and I wish you all the best in your bright future.