Formation of Groups

Formations of the group are used to find the number of ways n distinct objects can be divided into m groups, whose sizes are known. The number of ways in which (m + n) distinct objects are divided into two groups of the size m and n is equivalent to the number of ways in which m objects are selected from (m + n) objects. The other group of n objects is formed from the remaining n objects.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is Formation of Groups?
2. Formation of Groups for (m+n+r) Distinct objects
3. Solved Example Based on Formation of Groups

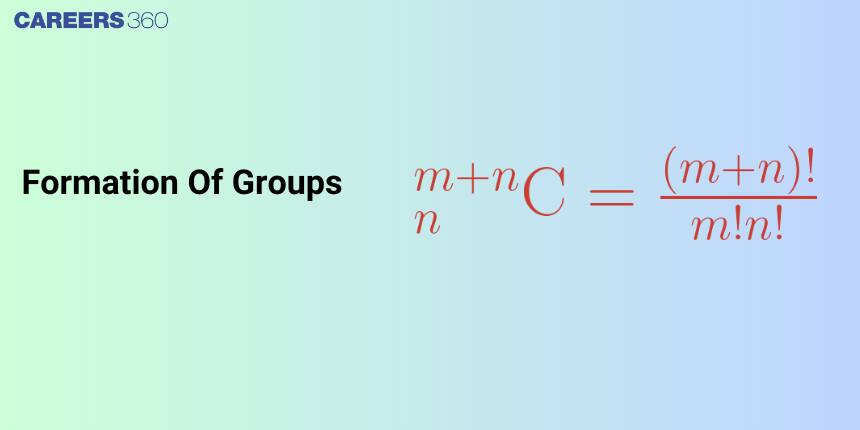
In this article, we will learn about the Formation of Groups. This topic falls under the broader category of Permutations and combinations, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE.

What is Formation of Groups?

Formations of the group are used to find the number of ways n distinct objects can be divided into m groups, whose sizes are known.

Consider that 12 people have to be divided among three groups of unequal sizes such as one group has 3 members, one group has 4 members and one group has 5 members.

We could have formed a group of 3 members in ${}^{12}{\mathrm{C}}_3$ ways. Having formed a group of three, we would be left with $12-3=9$ people. A group of 4 members can be formed from these 9 members in ${}^9{\mathrm{C}}_4$ ways. For each group of 3 members formed earlier, there would be further ${}^9{\mathrm{C}}_4$ ways of forming a group of four. Thus, the total possible number of ways of forming a group of 3 and a group of 4 would be ${}^{12}{\mathrm{C}}_3\times {}^9{\mathrm{C}}_4$. Now there would be 5 people left who are the third group i.e. the third group can be formed in only 1 way. To maintain consistency, we will say that the third group can be formed in ${}^5{\mathrm{C}}_5$ ways (which is 1 anyway). Thus, the total number of ways of forming the groups is ${}^{12}{\mathrm{C}}_3\times {}^9{\mathrm{C}}_4\times {}^5{\mathrm{C}}_5$. On expansion, this equals $\frac{(12)!}{3!4!5!}$.

Formation of Groups for (m+n+r) Distinct objects

• This concept can be generalized for (m+n+r) distinct objects which have to be grouped into three unequal groups containing m,n, and r objects. So this grouping can be done in $\frac{(\mathrm{m}+\mathrm{n}+\mathrm{r})!}{\mathrm{m}!\mathrm{n}!\mathrm{r}!}$ number of ways
• This same concept will apply for (m+n) distinct object which has to be grouped into two unequal containing m, and n items. Number of ways of dividing mn objects into m groups such that all groups contain n objects equals $\frac{(\mathrm{mn})!}{(\mathrm{n}!{)}^{\mathrm{m}}}\times \frac{1}{\mathrm{m}!}$

Example: How many ways 12 people can be divided into 3 groups, such that all three of them contain 4 people each?

Solution: The number of ways of forming the three groups is ${}^{12}{\mathrm{C}}_4\cdot {}^8{\mathrm{C}}_4\cdot {}^4{\mathrm{C}}_4$. Since we are multiplying these three factors, we are inadvertently also arranging the groups in a particular order. (Remember that if one position can be filled in 5 ways, another can be filled in 4 ways, and the third can be filled in 3 ways when we apply the rule of AND i.e. $5\times 4\times 3$, we are basically finding the number of "arrangements" of the three positions)

But the question requires us to just form groups and we do not have to “arrange” the groups. Since we arranged 3 objects that did not have to be arranged, we counted each unique way of forming the groups 3! times i.e. 6 times. Thus, the correct answer would be found by dividing the earlier found answer by 3! This will give you the above formula itself.

Recommended Video Based on Formation of Groups:

Solved Example Based on Formation of Groups

Example 1: The number of ways in which 10 identical balls can be distributed among 5 students so that each gets at least one is

Solution: Rule for distribution of identical objects into Groups:

The number of ways in which $n$ identical things can be distributed to $r$ people (when each gets at least one) is ${}^{n-1}{C}_{r-1}$

Now,
The number of ways $={}^{10-1}{C}_{5-1}={}^9{C}_4$.
Hence, the answer is ${}^9{C}_4$

Example 2: Out of a group of 8 students, 5 are to be arranged in a queue, among which particular 3 out of 8 must be there. Then the number of ways in which a queue can be formed is

Solution: According to the question, out of 8 students, 3 students are already fixed.
So out of the remaining 5 - and two more have to be included
No. of ways of selecting those two $={}^5{C}_2=10$
Now we have a total of 5 students, so these five can be arranged in 5! i.e 120 ways
$\therefore$ Total number of ways $=120\times 10=1200$

Now we have a total of 5 students, so these five can be arranged in 5 ! i.e 120 ways
$\therefore$ Total number of ways $=120\times 10=1200$
Hence, the answer is 1200
Example 3: The number of ways of allotting three rooms in a hotel among 12 guests, where one room has a capacity of 3 , the second has a capacity of 4 , and the third has a capacity of 5 is

Solution: Now,

Firstly, 12 people have to be divided into three groups of 3,4 and 5
No. of ways of grouping $=\frac{12!}{3!4!5!}$
After division allotment can be done only in one way

$\text{ Total number of ways }=\frac{(12)!}{(3)!(4)!(5)!}=27720$

Hence, the answer is 27720

Example 4: The number of ways in which 6 distinct objects can be kept in two identical boxes so that no box remains empty is

Solution: Initially consider the boxes $B_1$ and $B_2$ to be distinct.
Object ' a ' can be kept in either of the boxes in 2 ways, similarly for all other things $\Rightarrow$ Total ways $=2^6$
But this includes when all the things are in $B_1$ or $B_2\Rightarrow$ Number of ways $=2^6-2$
Since the boxes are identical, therefore,

$\frac{2^6-2}{2}=2^5-1=31$

Hence, the answer is 31

Example 5: There are 9 chairs placed along a row. If there are 5 girls and 4 boys, then in how many ways can they sit such that all girls sit together and all boys sit together?

Solution: Put all the girls in one box and the boys in another box 5G 4B These two boxes can be arranged in 2 ! ways. In the first box, the 5 girls will arrange themselves in 5 ! ways, and in the other box, the boys will rearrange themselves in 4! ways.
$\therefore$ Total number of ways $=2!4!5$ !
Hence, the answer is $2!4!5$ !