Length of Sub-Tangent and Sub-Normal of an Ellipse

An ellipse is the locus of a point which moves such that its distance from a fixed point (focus) gives a constant. The tangent of an ellipse is a line which touches the ellipse at only one point without passing through it. This concept length of sub-tangent and sub-normal of an ellipse is used in to determine important properties of the ellipse.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

In this article, we discuss the director circle of ellipses which falls under the topic of two dimensional Analytical Geometry. It is an important topic for not only board exam but also for the competitive exams.

Ellipse

An ellipse is the locus of a point which moves such that its distance from a fixed point (focus) gives a constant. The standard form of the equation of an ellipse with centre $(0,0)$ and major axis on the x -axis is $\frac{\mathrm{x}^2}{\mathbf{a}^2}+\frac{\mathbf{y}^2}{\mathbf{b}^2}=1 \quad$ where $\mathrm{b}^2=\mathrm{a}^2\left(1-\mathrm{e}^2\right)$
1. $a>b$
2. the length of the major axis is $2 a$
3. the length of the minor axis is $2 b$
4. the coordinates of the vertices are $( \pm a, 0)$

Tangent of an Ellipse

Tangent of an ellipse is a line which touches the ellipse at only one point.

For any point $\left(x_1, y_1\right)$ on the ellipse, the equation of the tangent line at that point is given by:

$
\frac{x_1 x}{a^2}+\frac{y_1 y}{b^2}=1
$

Normal at a point of an Ellipse

Normal at a point of the ellipse is a line perpendicular to the tangent and passing through the point of contact. The equation of normal at $\left(x_1, y_1\right)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is

$
\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2
$

Length of sub-Tangent and sub-Normal of an Ellipse

The sub-Tangent and sub-Normal are particular portions of the tangent line and normal line respectively. The portion of the tangent along the x-axis from the point of contact of the tangent on the ellipse to the intersection of the tangent at the x-axis is called the sub-Tangent. Similarly, the portion of the normal along the x-axis from the point of contact of the tangent on the ellipse to the intersection of the normal at the x-axis is called the sub-Normal.

The tangent and normal of the ellipse at P(x₁ , y₁) meet the X-axis at Q and R respectively

Then, the equation of the tangent at $P\left(x_1, y_1\right)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is:

$
\frac{\mathrm{xx}_1}{\mathrm{a}^2}+\frac{\mathrm{yy}_1}{\mathrm{~b}^2}=1
$

$\because Q$ lies on X -axis, then put $\mathrm{y}=0$ in $\mathrm{Eq}(\mathrm{i})$, we get
$\Rightarrow \mathrm{x}=\mathrm{OQ}$
$\Rightarrow \mathrm{OQ}=\frac{\mathrm{a}^2}{\mathrm{x}_1}$ and $\mathrm{OS}=\mathrm{x}_1$

$
\text { length of subtangent }=S Q=O Q-O S=\frac{a^2}{x_1}-x_1
$

Equation of normal at $P\left(x_1, y_1\right)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is

$
\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2
$
$\Rightarrow \mathrm{x}=\mathrm{OR}$
$\therefore \mathrm{OR}=\mathrm{x}_1-\frac{\mathrm{b}^2}{\mathrm{a}^2} \mathrm{x}_1$
$\therefore$ Length of Subnormal $=$ RS $=$ OS - OR

$
\begin{aligned}
& =x_1-\left(x_1-\frac{b^2}{a^2} x_1\right) \\
& =\frac{b^2}{a^2} x_1=\left(1-e^2\right) x_1
\end{aligned}
$

Recommended Video Based on Length of Sub-Tangent and Sub-Normal of Ellipse

Solved Examples based on Length of Sub-Tangent and Sub-Normal of Ellipse

Example 1: If the normal to the ellipse $3 x^2+4 y^2=12$ at a point P on its parallel to the line, $2 x+y=4$ and the tangent to the ellipse at P passes through $Q(4,4)$ then PQ is equal to :
1)$
\frac{\sqrt{157}}{2}
$

2)$
\frac{\sqrt{221}}{2}
$

3)$
\frac{\sqrt{61}}{2}
$

4) $\frac{5 \sqrt{5}}{2}$

Solution

Equation of Norma to ellipse -
The equation of normal at $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to the ellipse, $\frac{\mathrm{A}}{\mathrm{a}^2}+\frac{y}{\mathrm{~b}^2}=1$ is $\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$.

Distance formula -
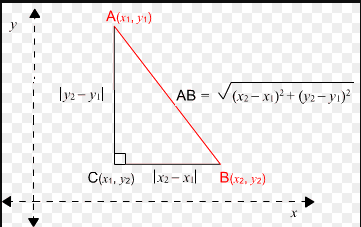
The distance between the point $A\left(x_1, y_1\right)$ and $B\left(x_2, y_2\right)$
is $\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$
- wherein

$
\begin{aligned}
& 3 x^2+4 y^2=12 \\
& \frac{x^2}{4}+\frac{y^2}{3}=1
\end{aligned}
$

So, $x=2 \cos \theta \quad y=\sqrt{3} \sin \theta$
Let $\quad P(2 \cos \theta, \sqrt{3} \sin \theta)$
Equation of normal is $\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$

$
\begin{aligned}
& \frac{4 x}{2 \cos \theta}-\frac{3 y}{\sqrt{3} \sin \theta}=4-3 \\
& 2 x \sin \theta-\sqrt{3} y \cos \theta=\cos \theta \sin \theta \\
& \text { Slope }=\frac{2}{\sqrt{3}} \tan \theta=-2 \\
& \tan \theta=-\sqrt{3}
\end{aligned}
$

Equation of tangent is it passes through $(4,4)$
$12 \cos \theta+8 \sqrt{3} \sin \theta=6$

$
\begin{aligned}
& \frac{1}{2} \cos \theta+\frac{8 \sqrt{3}}{6} \sin \theta=1 \\
& \cos \theta=-\frac{1}{2}, \quad \sin \theta=\frac{\sqrt{3}}{2} \quad \therefore \theta=120^{\circ}
\end{aligned}
$

Hence point is $(2 \cos 120, \sqrt{3} \sin 120)$

$
\begin{aligned}
& P\left(-1, \frac{3}{2}\right), Q(4,4) \\
& P Q=\sqrt{(-1-4)^2+\left(\frac{3}{2}-4\right)^2}=\sqrt{25+\frac{25}{4}} \\
& =\frac{5 \sqrt{5}}{2}
\end{aligned}
$

Example 2: Let the tangents at the points P and Q on the ellipse $\frac{\mathrm{x}^2}{2}+\frac{\mathrm{y}^2}{4}=1$ meet at the point $\mathrm{R}(\sqrt{2}, 2 \sqrt{2}-2)$. If S is the focus of the ellipse on its negative major axis, then $\mathrm{SP}^2+\mathrm{SQ}^2$ is equal to $\qquad$
MAINS 2022]
Solution
Equation of chard of contact is $\mathrm{T}=0$

$
\begin{aligned}
& \Rightarrow \quad \frac{\sqrt{2} \mathrm{x}}{2}+\frac{(2 \sqrt{2}-2) \mathrm{y}}{4}=1 \\
& \Rightarrow \quad 2 \sqrt{2} \mathrm{x}+(2 \sqrt{2}-2) \mathrm{y}=4 \\
& \Rightarrow \quad \mathrm{x}=\frac{4-(2 \sqrt{2}-2) \mathrm{y}}{2 \sqrt{2}}
\end{aligned}
$
Finding point of intersection with ellipse

$
\begin{aligned}
& \frac{(4-(2 \sqrt{2}-2) \mathrm{y})^2}{8 \times 2}+\frac{y^2}{4}=1 \\
& \Rightarrow \frac{(2-(\sqrt{2}-1) \mathrm{y})^2}{4}+\frac{\mathrm{y}^2}{4}=1 \\
& \Rightarrow \quad 4+(\sqrt{2}-1)^2 \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}+\mathrm{y}^2=4 \\
& \Rightarrow \quad(3-2 \sqrt{2}+1) \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}=0 \\
& \Rightarrow \quad 2 \sqrt{2}(\sqrt{2}-1) \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}=0 \\
& \Rightarrow 2 \sqrt{2}(\sqrt{2}-1) \mathrm{y}(\mathrm{y}-\sqrt{2})=0 \\
& \Rightarrow \mathrm{y}=0, \sqrt{2} \\
& \Rightarrow \mathrm{x}=\sqrt{2}, 1
\end{aligned}
$

$
\begin{aligned}
& \frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2 e^2 \\
& \frac{a^2 x}{a e}-\frac{b^2 y}{b^2} \cdot a=a^2 e^2 \\
& \frac{a x}{e}-a y=a^2 e^2 \Rightarrow \frac{x}{e}-y=a e^2
\end{aligned}
$

passes through $(0, b)$

$
\begin{aligned}
-b=a e^2 & \Rightarrow b^2=a^2 e^4 \\
a^2\left(1-e^2\right) & =a^2 e^4 \Rightarrow e^4+e^2=1
\end{aligned}
$

$
\begin{aligned}
& \Rightarrow \mathrm{x}=\sqrt{2}, 1 \\
& \therefore \mathrm{P}(\sqrt{2}, 0), \mathrm{Q}(1, \sqrt{2})
\end{aligned}
$
S is $(0,-\mathrm{be})$

$
\begin{aligned}
& \mathrm{e}=\sqrt{1-\frac{2}{4}}=\frac{1}{\sqrt{2}} \\
& \therefore \mathrm{S} \text { is }(0,-\sqrt{2}) \\
& \therefore \mathrm{PS}^2+\mathrm{SQ}^2=4+9=13
\end{aligned}
$

Hence, the answer is 13 .

Example 3: If the normal at the point $\mathrm{P}(\theta)$ to the ellipse $\frac{\mathrm{x}^2}{14}+\frac{\mathrm{y}^2}{5}=1$ intersects it again at the point $\mathrm{Q}(2 \theta)$, then $\cos \theta$ is equal to
1) $2 / 3$
2) $-2 / 3$
3) $3 / 4$
4) None of these

Solution

$
\begin{aligned}
& \frac{\sqrt{14} \mathrm{x}}{\cos \theta}-\frac{\sqrt{5} \mathrm{y}}{\sin \theta}=14-5 ; \text { as it passes through }(\sqrt{14} \cos 2 \theta, \sqrt{5} \sin 2 \theta) \\
& \text { so, } \frac{14\left(2 \cos ^2 \theta-1\right)}{\cos \theta}-\frac{5 \times 2 \sin \theta \cos \theta}{\sin \theta}=9 \\
& \Rightarrow 28 \cos \theta-\frac{14}{\cos \theta}-10 \cos \theta=9 \\
& \Rightarrow 18 \cos ^2 \theta-9 \cos \theta-14=0 \\
& \Rightarrow(3 \cos \theta+2)(6 \cos \theta-7)=0 \Rightarrow \cos \theta=-\frac{2}{3}
\end{aligned}
$
Hence, the answer is the option (2).

Example 4: Let the tangent and normal at the point $(3 \sqrt{3}, 1)$ on the ellipse $\frac{x^2}{36}+\frac{y^2}{4}=1$ meet the $y$-axis at the points $A$ and $B$ respectively. Let the circle $C$ be drawn taking $A B$ as a diameter and the line $\mathrm{x}=2 \sqrt{5}$ intersect C at the points P and Q . If the tangents at the points P and Q on the circle intersect at the point $(\alpha, \beta)$, then $\left(\alpha^2-\beta^2\right)$ is equal to [JEE MAINS 2023]
Solution

Given ellipse $\frac{x^2}{36}+\frac{y^2}{4}=1$
$\frac{\mathrm{x}}{4 \sqrt{3}}+\frac{\mathrm{y}}{4}=1$
$\mathrm{y}=4$
$\frac{x}{4}-\frac{4}{4 \sqrt{3}}=\frac{2}{\sqrt{3}}$
$y=-8$
$
\begin{aligned}
& \mathrm{h} x+\mathrm{ky}+2(\mathrm{y}+\mathrm{k})-32=0 \\
& \mathrm{k}=-2 \\
& \mathrm{hx}+2 \mathrm{k}-32=0 \\
& \mathrm{hx}=36 \\
& \alpha=\mathrm{h}=\frac{36}{2 \sqrt{5}} \\
& \beta=\mathrm{k}=-2 \\
& \alpha^2-\beta^2=\frac{304}{5}
\end{aligned}
$
Hence, the answer is 304 / 5

Example 5: If m is the slope of a common tangent to the curves $\frac{\mathrm{x}^2}{16}+\frac{\mathrm{y}^2}{9}=1$ and $\mathrm{x}^2+\mathrm{y}^2=12$, then $12 \mathrm{~m}^2$ is equal to :
[JEE MAINS 2022]
Solution

$
\begin{aligned}
& \frac{x^2}{16}+\frac{y^2}{9}=1 \\
& \therefore \quad 16 m^2+9=\mathrm{m} x \pm \sqrt{12 \mathrm{~m}^2+12} \\
& \mathrm{~m}^2=\frac{3}{4} \\
& \therefore 12 \mathrm{~m}^2=9
\end{aligned}
$
$
\begin{array}{ll}
\because & x^2+y^2=12 \\
\therefore & y=m x \pm \sqrt{2 m^2+12}
\end{array}
$

Hence, the answer is 9

Summary:

The lengths of the sub-Tangent and sub-Normal is used to determine the nature of the tangent and the curve respectively. This concept is used to determine the other properties of the eliipse. In real life, this can be used to manufacture optical instruments as they are used to determine the angle of incidence, reflection and refraction.