Matrix Multiplication

Matrix multiplication: Definition

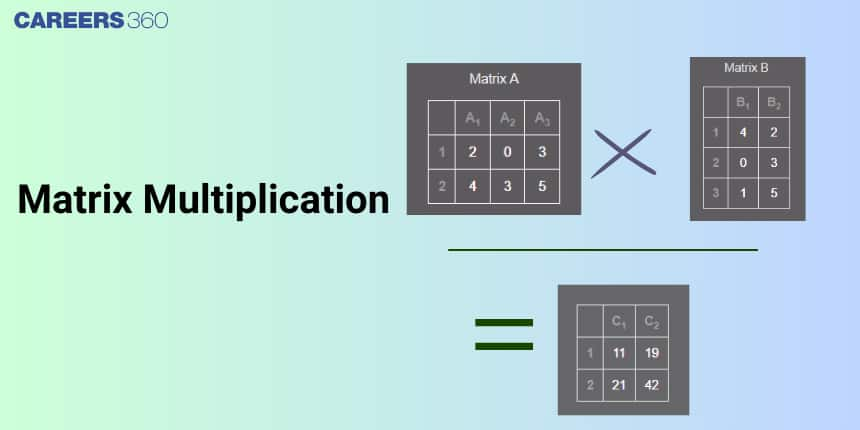
Matrix multiplication is a method of combining two matrices by multiplying rows of the first matrix with columns of the second. If $A = [a_{ij}]$ is a matrix of order $m \times n$ and $B = [b_{ij}]$ is a matrix of order $n \times p$, then the product $C = AB$ is defined as a matrix of order $m \times p$, where each element $c_{ij}$ is given by:

$c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj}$

This means that to calculate the element in the $i$-th row and $j$-th column of $C$, we multiply the elements of the $i$-th row of $A$ with the corresponding elements of the $j$-th column of $B$, and then add them together.

The product of the two matrices $A$ and $B$, if they are $A$ and $B$, is represented as : $X=A B$. As a result, the two matrices' product equals their dot product.

Order of the Product Matrix

• If $A$ is of order $m \times n$ and $B$ is of order $n \times p$, then $AB$ will be of order $m \times p$.

• The number of columns in the first matrix must equal the number of rows in the second for multiplication to be possible.

Example: Let $A = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}, \quad B = \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix}$

Here, $A$ is of order $1 \times 3$ and $B$ is of order $3 \times 1$, so the product $AB$ will be of order $1 \times 1$:

$AB = [1 \cdot 4 + 2 \cdot 5 + 3 \cdot 6] = [32]$

Thus, the product of a row matrix and a column matrix gives a single number, also called a scalar result.

Conditions for Matrix Multiplication

For two matrices $A$ and $B$, the product $AB$ is defined only when the number of columns of $A$ equals the number of rows of $B$.

• If $A$ is of order $m \times n$ and $B$ is of order $n \times p$, then $AB$ exists and is of order $m \times p$.

• If this condition is not satisfied, the multiplication is not possible.

Example of Valid Multiplication:

$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}_{2 \times 2}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}_{2 \times 2}$

Here, $A$ is $2 \times 2$, $B$ is $2 \times 2$. Since columns of $A$ = rows of $B$, $AB$ exists (order $2 \times 2$).

Example of Invalid Multiplication:

$P = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}_{2 \times 3}, \quad Q = \begin{bmatrix} 7 & 8 \\ 9 & 10 \end{bmatrix}_{2 \times 2}$

Here, $P$ is $2 \times 3$ and $Q$ is $2 \times 2$. Since columns of $P \neq$ rows of $Q$, the product $PQ$ does not exist.

Types of Matrix Multiplication

Matrix multiplication can be performed in different ways depending on the type of operation involved. The main types of matrix multiplication include row by column multiplication, scalar multiplication, and special cases like square, identity, and zero matrices. These variations help in solving different mathematical problems. Below are the main types of matrix multiplication.

Matrix Multiplication by scalar

When a constant $k$ (scalar) multiplies a matrix $A = [a_{ij}]$, each element is multiplied by $k$:

$kA = [k \cdot a_{ij}]$

Example:

$3 \cdot \begin{bmatrix} 1 & -2 \\ 0 & 5 \end{bmatrix} = \begin{bmatrix} 3 & -6 \\ 0 & 15 \end{bmatrix}$

Let $\mathrm{k}$ be any scalar number, and $A=\left[a_{i j}\right]_{m \times n}$ be a matrix. Then the matrix is obtained by multiplying every element $\mathrm{A}$ by a scalar $\mathrm{k}$ and denoted as $\mathrm{kA}$.
$
\begin{aligned}
& k A=\left[k a_{i j}\right]_{m \times n} \\
& \qquad \mathrm{~A}=\left[\begin{array}{ll}
2 & 6 \\
3 & 7 \\
5 & 8
\end{array}\right] \text { then, } 3 \mathrm{~A}=\left[\begin{array}{ll}
3 \times 2 & 3 \times 6 \\
3 \times 3 & 3 \times 7 \\
3 \times 5 & 3 \times 8
\end{array}\right]=\left[\begin{array}{cc}
6 & 18 \\
9 & 21 \\
15 & 24
\end{array}\right]
\end{aligned}
$

Properties of scalar multiplication:

If $A$ and $B$ are two matrices and $k, l$ are scalar then
i) $k(A+B)=k A+k B$
ii) $k(A)=k(I A)=l(k A)$
iii) $(k+1) A=k A+1 A$
iv) $(-k) A=-(k A)=k(-A)$
v) $1 \mathrm{~A}=\mathrm{A},(-1) \mathrm{A}=-\mathrm{A}$

Note: $A$ and $B$ have the same order $m \times n$.

Row by Column Multiplication

This is the standard multiplication method where the $i$-th row of the first matrix is multiplied with the $j$-th column of the second.

For $A = [a_{ij}]{m \times n}$ and $B = [b{ij}]_{n \times p}$,

$c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj}$

Product $A B$ can be found if the number of columns in matrix $A$ and the number of rows in matrix $B$ are equal. Otherwise, multiplication $A B$ is not possible.
i) $A B$ is defined only if $\operatorname{col}(A)=\operatorname{row}(B)$
ii) $B A$ is defined only if $\operatorname{col}(B)=\operatorname{row}(A)$

If

$\begin{aligned} & \mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \\ & B=\left[b_{i j}\right]_{\mathrm{n} \times \mathrm{p}} \\ & \mathrm{C}=\mathrm{AB}=\left[\mathrm{c}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{p}} \\ & \text { Where } c_{i j}=\sum_{j=1}^n a_{i j} b_{j k}, 1 \leq \mathrm{i} \leq \mathrm{m}, 1 \leq \mathrm{k} \leq \mathrm{p} \\ & =\mathrm{a}_{\mathrm{i} 1} \mathrm{~b}_{1 \mathrm{k}}+\mathrm{a}_{\mathrm{i} 2} \mathrm{~b}_{2 \mathrm{k}}+\mathrm{a}_{\mathrm{i} 3} \mathrm{~b}_{3 \mathrm{k}}+\ldots+\mathrm{a}_{\mathrm{in}} \mathrm{b}_{\mathrm{nk}} \\ & \end{aligned}$

For example:

Suppose, two matrices are given
$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{33}
\end{array}\right]_{2 \times 3} \quad \text { and } \quad \mathrm{B}=\left[\begin{array}{lll}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} & b_{32} & b_{33}
\end{array}\right]_{3 \times 3}
$

To obtain the entries in row $i$ and column j of AB, we multiply the entries in row $i$ of $\mathrm{A}$ by column $j$ in $\mathrm{B}$ and add.
given matrices $\mathrm{A}$ and $\mathrm{B}$, where the order of $\mathrm{A}$ are $2 \times 3$ and the order of $\mathrm{B}$ are $3 \times 3$, the product of $\mathrm{AB}$ will be a $2 \times 3$ matrix.To obtain the entry in row 1, column 1 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the first column in $\mathrm{B}$, and add.

$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{11} \\
b_{21} \\
b_{31}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{11}+\mathrm{a}_{12} \cdot \mathrm{b}_{21}+\mathrm{a}_{13} \cdot \mathrm{b}_{31}
$

To obtain the entry in row 1, column 2 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the second column in B and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{12} \\
b_{22} \\
b_{32}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{12}+\mathrm{a}_{12} \cdot \mathrm{b}_{22}+\mathrm{a}_{13} \cdot \mathrm{b}_{32}
$

To obtain the entry in row 1, column 3 of $\mathrm{AB}$, multiply the first row in $A$ by the third column in B, and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{13} \\
b_{23} \\
b_{33}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{13}+\mathrm{a}_{12} \cdot \mathrm{b}_{23}+\mathrm{a}_{13} \cdot \mathrm{b}_{33}
$

We proceed the same way to obtain the second row of $\mathrm{AB}$. In other words, row 2 of $\mathrm{A}$ times column 1 of $\mathrm{B}$; row 2 of A times column 2 of B; row 2 of A times column 3 of B.

When complete, the product matrix will be
$
\mathrm{AB}=\left[\begin{array}{lll}
a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31} & a_{11} \cdot b_{12}+a_{12} \cdot b_{22}+a_{13} \cdot b_{32} & a_{11} \cdot b_{13}+a_{12} \cdot b_{23}+a_{13} \cdot b_{33} \\
a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31} & a_{21} \cdot b_{12}+a_{22} \cdot b_{22}+a_{23} \cdot b_{32} & a_{21} \cdot b_{13}+a_{22} \cdot b_{23}+a_{23} \cdot b_{33}
\end{array}\right]
$

Matrix multiplication rules

The following matrix multiplication rules and properties can be expressed using the above-described formula and process.

• If the number of rows in B equals the number of columns in A, then the product of two matrices A and B is defined.
• BA does not need to be defined if AB is defined.
• Both AB and BA are defined if A and B are square matrices of the same order.
• It is not required for AB to equal BA if both AB and BA are defined.
• One of the matrices is not required to be a zero matrix in order for the product of two matrices to be a zero matrix.

Properties of matrix multiplication:

i) Multiplication may or may not be commutative, so AB may or may not be equal to $BA$
ii) Matrix multiplication is associative, meaning $A(B C)=(A B) C$
iii) Matrix multiplication is distributive over addition, mean $A(B+C)=A B+A C$ and $(B+C) A=B A+C A$
iv) If matrix multiplication of two matrices gives a null matrix then it doesn't mean that any of those two matrices was a null matrix.

$A=\left[\begin{array}{ll}0 & 2 \\ 0 & 0\end{array}\right]$ and $B=\left[\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right]$, then $A B=\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$

v) Cancellation law in matrix multiplication doesn't hold, which means $A B=A C \Rightarrow B$ $=\mathrm{C}$
vi) Matrix multiplication $A \times A$ is represented by $A^2$. Thus, $A \cdot A \cdot A \cdot A$ .........$n$ times $=A^n$.

vii) if $\mathrm{A}$ is $\mathrm{m} \times \mathrm{n}$ matrix then, $\mathrm{I}_{\mathrm{m}} \mathrm{A}=\mathrm{A}=\mathrm{AI}_{\mathrm{n}}$.

Special Cases

1. Square Matrices: Multiplication of square matrices of the same order is always possible.

2. Identity Matrix ($I$): $AI = IA = A$ for any compatible matrix $A$.

3. Zero Matrix ($O$): $AO = OA = O$, where $O$ is the zero matrix of suitable order.

Solved Example based on Multiplication of matrices

Example 1: Let $\mathrm{A}=\left[\mathrm{a}_{i j}\right]$ be a square matrix of order 3 such that $\mathrm{a}_{i j}=2^{j-i}$, for all $i, j=1,2,3$. Then, the matrix $\mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}$ is equal to: [JEE-2022]
Solution: Forming matrix A using the given $\mathrm{A}=\left[\mathrm{a}_{i j}\right]$ formula
$
\begin{aligned}
& \mathrm{A}=\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right] \\
& \mathrm{A}^2=\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right] \\
& =\left[\begin{array}{ccc}
3 & 6 & 12 \\
3 \cdot 2^{-1} & 3 & 6 \\
3 \cdot 2^{-2} & 3 \cdot 2^{-1} & 3
\end{array}\right]=3 \mathrm{~A}
\end{aligned}
$

$
\begin{aligned}
& \therefore \mathrm{A}^2=3 \mathrm{~A} \\
& \Rightarrow \mathrm{A}^3=\mathrm{A}^2 \cdot \mathrm{A}=3 \mathrm{~A} \cdot \mathrm{A}=3 \mathrm{~A}^2=3 \cdot 3 \mathrm{~A}=3^2 \mathrm{~A} \\
& \Rightarrow \mathrm{A}^4=\mathrm{A}^2 \cdot \mathrm{A}^2=3 \mathrm{~A} \cdot 3 \mathrm{~A}=3^2 \mathrm{~A}^2=3^2 \cdot 3 \mathrm{~A}=3^3 \mathrm{~A}
\end{aligned}
$

Similarly $\mathrm{A}^5=3^4 \mathrm{~A}, \cdots \cdot \mathrm{A}^{10}=3^9 \mathrm{~A}$
$
\begin{aligned}
& \therefore \mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}=\mathrm{A}\left(3+3^2+\cdots+3^9\right) \\
& =\frac{3\left(3^9-1\right)}{3-1} \mathrm{~A} \\
& =\left(\frac{3^{10}-3}{2}\right) \mathrm{A} \text {. } \\
&
\end{aligned}
$

Hence, the matrix $\mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}$ is equal to $=\left(\frac{3^{10}-3}{2}\right) \mathrm{A}$.

Example 2: Let $\mathrm{M}=\left[\begin{array}{cc}0 & -\alpha \\ \alpha & 0\end{array}\right]$, where $\alpha$ is a non-zero real number and $N=\sum_{k=1}^{49} \mathrm{M}^{2 \mathrm{k}}$. If $\left(\mathrm{I}-\mathrm{M}^2\right) \mathrm{N}=-2 \mathrm{I}$, then the positive integral value of $\alpha$ is [JEE-2022]

Solution:
$
\begin{aligned}
& \mathrm{M}=\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right] \\
& \mathrm{M}^2=\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right]\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right] \\
&=\left[\begin{array}{cc}
-\alpha^2 & 0 \\
0 & -\alpha^2
\end{array}\right] \\
&=-\alpha^2 \cdot \mathrm{I} \\
& \therefore \mathrm{M}^4=\mathrm{M}^2 \cdot \mathrm{M}^2=\alpha^4 \mathrm{I} \\
& \mathrm{M}^6=\mathrm{M}^4 \cdot \mathrm{M}^2=-\alpha^6 \mathrm{I} \\
&\ldots . . \\
&\ldots . . \\
& \therefore \mathrm{N}=\mathrm{M}^2+\mathrm{M}^4+\mathrm{M}^6+--+\mathrm{M}^{98}
\end{aligned}
$

$
\begin{aligned}
& =-\alpha^2 \mathrm{I}+\alpha^4 \mathrm{I}-\alpha^6 \mathrm{I} \ldots . .49 \text { terms } \\
& =\left(-\alpha^2+\alpha^4-\alpha^6-\ldots\right) \mathrm{I} \\
& =-\alpha^2\left(\frac{\left(-\alpha^2\right)^{49}-1}{-\alpha^2-1}\right) \mathrm{I}
\end{aligned}
$
$
\begin{aligned}
& \text { Given }\left(\mathrm{I}-\mathrm{M}^2\right) \mathrm{N}=-2 \mathrm{I} \\
& \Rightarrow\left(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{cc}
-\alpha^2 & 0 \\
0 & -\alpha^2
\end{array}\right]\right)\left(\frac{\alpha^2\left(-\alpha^{98}-1\right)}{\left(\alpha^2+1\right)}\right) \mathrm{I}=-2 \mathrm{I} \\
& \Rightarrow\left(1+\alpha^2\right) \mathrm{I} \cdot \frac{\alpha^2\left(-\alpha^{98}-1\right)}{\left(\alpha^2+1\right)}=-2 \mathrm{I} .
\end{aligned}
$

Only $\alpha=1$ satisfies it.
$
\Rightarrow \quad \alpha^2\left(-\alpha^{98}-1\right)=-2
$

Hence, the positive integral value of $\alpha$ is 1

Example 3: If $p=\left[\begin{array}{cc}\frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2}\end{array}\right], \mathrm{A}=\left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]$ and $\mathrm{Q}=\mathrm{PAP}^{\top}$, then $\mathrm{P}^{\top} \mathrm{Q}^{2015} \mathrm{P}$ is:

Solution:

$P^T Q^{2015} P$

$= P^T Q \cdot Q \cdot Q \cdot \ldots \cdot Q P$

$(2015 \text{ times})$

Now, if $P = \begin{bmatrix} \tfrac{\sqrt{3}}{2} & \tfrac{1}{2} \\ -\tfrac{1}{2} & \tfrac{\sqrt{3}}{2} \end{bmatrix}$

then,

$P^T P = \begin{bmatrix} \tfrac{\sqrt{3}}{2} & -\tfrac{1}{2} \\ \tfrac{1}{2} & \tfrac{\sqrt{3}}{2} \end{bmatrix} \cdot \begin{bmatrix} \tfrac{\sqrt{3}}{2} & \tfrac{1}{2} \\ -\tfrac{1}{2} & \tfrac{\sqrt{3}}{2} \end{bmatrix}$

$= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I$

$\Rightarrow P^T Q^{2015} P = A^{2015}$

$= \underbrace{\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \cdot \ldots \cdot \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}}_{2015 \text{ times}}$

$= \begin{bmatrix} 1 & 2015 \\ 0 & 1 \end{bmatrix}$

Example 4: Let where $\mathrm{i}=\sqrt{-1}$. Then, the number of elements in the set $\left\{\mathrm{n} \in\{1,2, \ldots, 100\}: \mathrm{A}^{\mathrm{n}}=\mathrm{A}\right\}$ is [JEE-2017]
Solution:
$
\begin{aligned}
& A^2=\left[\begin{array}{cc}
1+i & 1 \\
-i & 0
\end{array}\right]\left[\begin{array}{cc}
1+i & 1 \\
-i & 0
\end{array}\right] \\
& =\left[\begin{array}{cc}
(1+i)^2-i & 1+i \\
-i+1 & -i
\end{array}\right] \\
& =\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right] \\
& \mathrm{A}^4=\mathrm{A}^2 \cdot \mathrm{A}^2 \\
& =\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right]\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right] \\
& =\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]=I \\
& \therefore \mathrm{A}^4=\mathrm{I} . \\
& \Rightarrow \mathrm{A}^{4 \mathrm{p}+1}=\left(\mathrm{A}^4\right)^{\mathrm{p}} \cdot \mathrm{A}=\mathrm{I} \cdot \mathrm{A}=\mathrm{A}
\end{aligned}
$
$\therefore \mathrm{n}$ should be of type $4 \mathrm{p}+1$

$
\mathrm{n}=1,5,9, \ldots, 97
$

Hence, the number of elements in the set $\left\{\mathrm{n} \in\{1,2, \ldots, 100\}: \mathrm{A}^{\mathrm{n}}=\mathrm{A}\right\}$ is 25 .

Example 5: The total number of matrices $ A=\left(\begin{array}{ccc} 0 & 2 y & 1 \\ 2 x & y & -1 \\ 2 x & -y & 1 \end{array}\right),(x, y \in R, x \neq y)_{\text {for which }} A^T A=3 I_3 \text { is : } $

Solution:

$A=\begin{bmatrix}0&2y&1\\2x&y&-1\\2x&-y&1\end{bmatrix}$

Compute $A A^T$ and compare with $3I_3$:

$A A^T=\begin{bmatrix}
4y^2+1 & 2y^2-1 & -2y^2+1\\
2y^2-1 & 4x^2+y^2+1 & 4x^2-y^2-1\\
-2y^2+1 & 4x^2-y^2-1 & 4x^2+y^2+1
\end{bmatrix}$

Off-diagonal $=0$ gives $2y^2-1=0$ and $4x^2-y^2-1=0$.

$y^2=\tfrac12$, hence $4x^2=\tfrac12+1=\tfrac32\Rightarrow x^2=\tfrac38$.

Diagonal $=3$ is consistent: $4y^2+1=3$, $4x^2+y^2+1=3$.

Thus $x=\pm\sqrt{\tfrac38}$, $y=\pm\tfrac1{\sqrt2}$, and $x\ne y$ automatically since $\tfrac38\ne\tfrac12$.

Number of sign choices $=2\times2=4$.

List of topics related to Matrix Multiplication

Matrix multiplication connects to several advanced concepts in linear algebra and its applications in different fields. Below are the important topics related to matrix multiplication.

NCERT Resources

NCERT resources give step-by-step guidance and reliable practice material for mastering matrices in Class 12 Mathematics. They cover notes, solutions, and exemplar problems to build strong concepts. Below are the NCERT resources for Chapter 3 – Matrices.

NCERT Class 12 Maths Notes for Chapter 3 - Matrices

NCERT Solutions for Class 12 Maths for Chapter 3 - Matrices

NCERT Exemplar Class 12 Maths Solutions for Chapter 3 - Matrices

Practice Questions based on Matrix Multiplication

Practice questions are the best way to master matrix multiplication and apply its rules effectively. They help in gaining accuracy and speed for exams. Below are practice questions based on matrix multiplication.

Matrix Multiplication - Practice Question MCQ

You can practice questions on the related topics using the links shared below: