Onto Function: Definition, Properties, Examples

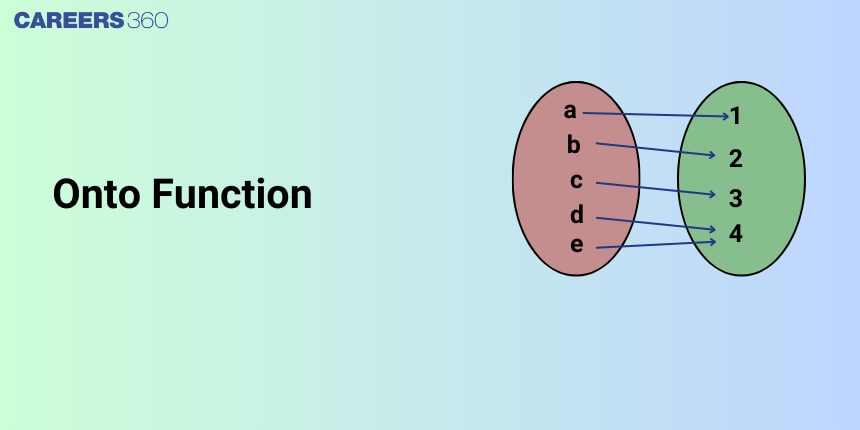
An onto function, also known as a surjective function, is a type of function where every element in the co-domain is mapped to at least one element in the domain. In other words, an onto function covers the entire codomain, ensuring that every possible output value is achieved by some input value.

In this article, we will explore the concept of onto functions, an important topic within the broader category of relations and functions, which is a crucial chapter in class 12 Mathematics. Understanding onto functions is essential not only for board exams but also for competitive exams such as the Joint Entrance Examination (JEE Main), SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the past ten years (2013 to 2023) in the JEE Main exam, a total of five questions have been asked on this concept: one in 2013, one in 2015, one in 2019, one in 2022, and one in 2023.

Onto function

A function $f: X \rightarrow Y$ is said to be onto (or surjective), if every element of $Y$ is the image of some element of $X$ under $f$, i.e., for every $y \in Y$, there exists an element $x$ in $X$ such that $f(x)=y$

Hence, Range = co-domain for an onto function

Example: Consider, $\mathrm{X}=\left\{\mathrm{x}_1, \mathrm{x}_2, \mathrm{x}_3, \mathrm{x}_4\right\}$ and $\mathrm{Y}=\left\{\mathrm{y}_1, \mathrm{y}_2, \mathrm{y}_3\right\}$

$
f: X \rightarrow Y
$

As every element in $Y$ has a pre-image in $X$, so it is an onto function

Method to show onto or surjective

Find the range of $y=f(x)$ and show that range of $f(x)=\operatorname{co}$-domain of $f(x)$

Properties of Onto Functions

1. Completeness: Every element of the codomain Y is the image of at least one element from the domain A.
2. Range and Codomain: For a function to be onto, its range (the set of all outputs) must be equal to its codomain.
3. Inverse Function: An onto function has a right inverse, meaning that there exists a function $g: Y \rightarrow X$ such that $f(g(y))=y$ for all $b \in Y$.

Number of Onto functions

If there is a function $f: A \rightarrow B_{\text {such that }} n(A)=m$ and $n(B)=n$, where $m \geq n$.
Then, the number of onto functions $=\displaystyle\sum_{r=1}^n(-1)^{n-r} n_{C_r} r^m$

If $A$ has $m$ elements and $B$ has $n$ elements, then the total number of onto functions can be calculated using the formula,
$n^m-\binom{n}{1}(n-1)^m+\binom{n}{2}(n-2)^m-\cdots+(-1)^{n-1}\binom{n}{n-1} 1^m$

We need to note that this formula will work only if $m ≥ n$. But if $m < n$, then the number of onto functions will be $0$ as it is not possible to use all the elements of $B$.
Therefore,

• if $n < m$, number of onto functions $= 0$
• if $n = m$, number of onto functions $= m!$

Example to Calculate Number of Onto Functions

If $A$ has $m$ elements and $B$ has $2$ elements, then the number of onto functions will be $2^{\mathrm{m}}-2$. This can be explained as:

• From a set of $m$ elements in $A$ to the set of $2$ elements in $B$, the total number of functions will be $2^{\mathrm{m}}$.
• And, out of these functions, $2$ functions are not onto, if all elements are mapped to the $1^{\text {st }}$ element of B or all elements are mapped to the $2^{\text {nd }}$ element of $B$.
• Thus, the total number of onto functions is $2^{\mathrm{m}}-2$.

Relationship Between Onto Function and One-to-One Function

Surjective and Injective functions are the different names for onto and one-to-one functions, respectively. The primary difference is that onto functions hit all the output values, whereas one-to-one functions are the ones where each $x$ is connected to only one $y$.

A function that is both One to One and Onto is called the bijective function. Each value of the output set is connected to the input set, and each output value is connected to only one input value.

Important Notes on Onto Function

Here is a list of a few points that should be remembered while studying onto function.

• A function is onto when its range and codomain are equal.
• Any function can be decomposed into an onto function or a surjection and an injection.

Recommended Video Based on Onto Functions

Solved Examples Based On the Onto Functions

Example 1: In the case of an onto function, which of the following is true?

1) Codomain = Range
2) Codomain $\subseteq$ Range
3) Range $\subseteq$ Codomain
4) None of these

Solution:

By the definition of onto function, we know that:

Co-domain = Range

Hence, the answer is the option (1).

Example 2: The number of functions f from {1,2,3,........,20} onto {1,2,3,........,20} such that f(k) is a multiple of 3, whenever k is a multiple of 4, is:

Solution:

Onto function -

If $f: A \rightarrow B$ is such that each \& every element in $B$ is the $f$ image of at least one element in $A$. Then it is the Onto function.
wherein
The range of $f$ is equal to Co - domain of $f$.

$
f(k)=3,6,9,12,15,18
$

for $\mathrm{k}=4,8,12,16,20$

$
\text { ways }=6 \times 5 \times 4 \times 3 \times 2 \times 1=6!
$
For remaining numbers $=(20-5)!=15$ !
Total ways $=15!\times 6$ !

Example 3: Let $A=\left\{x_1, x_2, x_3 \ldots . ., x_7\right\}$ and $B=\left\{y_1, y_2, y_3\right\}$ be two sets containing seven and three distinct elements respectively. Then the total number of functions $f: \mathrm{A} \rightarrow \mathrm{B}$ that are onto, if there exist exactly three elements x in A such that $f(\mathrm{x})=\mathrm{y}_2$, is equal to :

Solution:

As we learned in

Number of Onto functions -

$f: A \rightarrow B$

Such that $n(A)=m$
and $n(B)=n$

$m \geqslant n$

Number of onto functions

$=\displaystyle\sum_{r=1}^n(-1)^{n-r} n_{C_r} r^m$

No. of onto functions.
Since if there exist exactly three elements $x$ in $A$ which give a single image $y_2$. If this means four elements of $A$ will give an image of $y_1$ and $y_3$. So that $\left(2^4-2\right)$ of ${ }^7 C_3$

$=(16-2)^7 C_3=14 .^7 C_3$

Hence, the answer is $14 \cdot{ }^7 C_3$.

Example 4: If $n(A)=5$ and $n(B)=3$. Find the number of onto functions $A$ to $B$.

Solution:

$\begin{aligned}
& \sum_{r=1}^3(-1)^{3-r} C_r^3 \cdot r^5 \\
& =C_1^3-C_2^3\left(2^5\right)+C_3^3\left(3^5\right) \\
& =3-96+243 \\
& =150
\end{aligned}$

Hence, the answer is 150.

Example 5: If $n(A)=3$ and $n(B)=5$. Find the number of onto functions from $A$ to $B$.
Solution:
As we have learned
Number of Onto functions-
$f: A \rightarrow B$ such that $\mathrm{n}(\mathrm{A})=\mathrm{m}$ and $\mathrm{n}(\mathrm{B})=\mathrm{n}$, where:

$m \geqslant n$
Number of onto functions

$=\sum_{r=1}^n(-1)^{n-r} n_{C_r} r^m$
For onto function n(A)$>$ n(B). Otherwise, it will always be a into function.

Hence, there are zero onto functions.

Hence, the answer is 0.

Frequently Asked Questions(FAQ)-

1. What is the onto function?

Ans: An onto function is such that for every element in the codomain there exists an element in domain which maps to it.

2. How do you know if a function is onto?

Ans: $A$ function $f: A \rightarrow B$ is onto if, for every element $b \in B$, there exists an element $a \in A$ such that $f(a)=b$. To show that $f$ is an onto function, set $y=f(x)$, and solve for $x$, or show that we can always express $x$ in terms of $y$ for any $y \in B$.

3. What is the difference between into and onto function?

Ans: A function is called an Into function if there exists at least one element in the codomain of the function, which does not have a pre-image in the domain of the function. In an Onto function, no elements in the range are left unmapped. Each element in the range is associated with at least one element in the domain.

4. What is one example of an onto function?

Ans: For example, the function $f(x) = x + 1$ is a one-to-one function because it produces a different answer for every input.

5. Why is a function not onto?

Ans: When is a function not onto? If there is an element $y$ in the co-domain for which there is no x value in the domain such that $f(x) = y$.