Acceleration Of Block Against Friction

Imagine you are pushing a heavy box across the carpeted floor. The more force or effort in pushing that you put on the box, the more resistance it seems to give you against the movement. This is the force of friction, which opposes the motion of two or more materials involved with contact.

In this article, we will cover the concept of acceleration of block against friction. This concept falls under the broader category of the Law of motion which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of fourteen questions have been asked on this concept. And for NEET three questions were asked from this concept.

This Story also Contains

1. Acceleration Of Block Against Friction
2. Solved Example Based on Acceleration Of Block Against Friction
3. Summary

Acceleration Of Block Against Friction

There are mainly three cases of acceleration of a block on a horizontal surface. Let's start one by one.

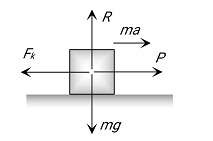
Case 1: Acceleration of a Block on a Horizontal Surface

When the body is moving under the application of force P, then kinetic friction opposes its motion.

Let a be the net acceleration of the body.

From the figure,

P−fk=maa=P−fkm

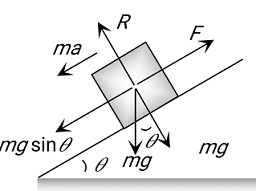
Case 2: Acceleration of a Block Sliding Down Over a Rough Inclined Plane

When the angle of the inclined plane is more than the angle of repose, the body placed on the inclined plane slides down with an acceleration a.

From the figure,

ma=mgsin⁡θ−fkma=mgsin⁡θ−μRma=mgsin⁡θ−μmgcos⁡θa=g[sin⁡θ−μcos⁡θ] For μ=0∴a=gsin⁡θ

Case 3: Retardation of a Block Sliding up Over a Rough Inclined Plane

When the angle of the inclined plane is less than the angle of repose, then for the upward motion (with some initial velocity)

ma=mgsin⁡θ+fkma=mgsin⁡θ+μmgcos⁡θma=g[sin⁡θ+μcos⁡θ]a=g[sin⁡θ+μcos⁡θ] For μ=0a=gsin⁡θ

Recommended Topic Video

Solved Example Based on Acceleration Of Block Against Friction

Example 1: In the given diagram if the force of 160 N is applied then what is the acceleration (in m/s²) of the block?

1) 4

2) 0

3) 6

4) 8

Solution:

Acceleration of Block on a horizontal surface -

ma=P−FKa=P−FKma= acceleration FK= kinetic friction - wherein

This is the case of acceleration against friction
fL=μsN⇒0.6∗200=120N N=mg=20×10=200 N
f>fL hence, the body will move

Kinetic friction fk will act on the body in the opposite direction.
∑f=ma160−80=20×aa=8020=4 m/s2

Example 2: A cylindrical vessel filled with water is released on an inclined surface of angle θ as shown in the figure. The friction coefficient of the surface with the vessel is μ(<tan⁡θ). Then the constant angle made by the surface of the water with the incline will be:

1) tan−1⁡μ 2) θ−tan−1⁡μ 3) θ+tan−1⁡μ 4) cot−1⁡μ

Solution:

Acceleration of Block sliding down over rough inclined plane -

ma=mgsin⁡θ−Fma=mgsin⁡θ−μRma=mgsin⁡θ−μmgcos⁡θa=[sin⁡θ−μcos⁡θ]

So using the above concept, below is the figure which shows forces acting on a 'particle' on the surface, with respect to the vessel.

(mgsin⁡θ and μmgcos⁡θ are pseudo forces)
tan⁡ϕ=μ∴ϕ=tan−1⁡μ

$\phi$ is the angle between the normal to the inclined surface and the resultant force. The same angle will be formed between the surface of the water & the inclined surface.

Example 3: A body of mass 2 kg slides down with an acceleration of 3 m/s2 on a rough inclined plane having a slope of 30∘. With what force along the plane(in N ), the block should be pulled to take the same body up the plane with the same acceleration: (g=10 m/s2)

1) 20

2) 14

3) 6

4) 4

Solution:

Given-

mass of the block, m=2kg

Accelerations of block in both cases, a=3m/s²

The angle of inclination, θ=30∘

Case -1: block sliding down-

From the figure,

ma=mgsin⁡θ−fkma=mgsin⁡θ−μRR=mgcos⁡θma=mgsin⁡θ−μmgcos⁡θa=g[sin⁡θ−μcos⁡θ]
substituting values-
3=10×(12−3μ2)μ=253

Case- 2: motion up the incline

Let us assume the block is pulled by applying force F as shown in the figure.

R=mgcos⁡θfk=μRF−fk−mgsin⁡θ=maF=fk+mgsin⁡θ+ma

Substituting the values-
F=253×20×32+20×12+2×3 F=20 N

Example 4:A block of mass 20 kg is kept on a rough horizontal surface. It is being pulled by applying 160N force horizontally as shown in the figure. The coefficient of static and kinetic friction between the block and surface respectively are 0.6 and 0.4. The acceleration (in m/s²) of the block is-(g=10m/s²)

1)4

2)8

3)2

4)1

Solution:

Given-

mass of the block, m=20 kg
Coefficients of friction, μs=0.6μk=0.4

Let the friction force acting on the block be f and acceleration be a.

F.B.D of the block-

For vertical equilibrium-

N=mg=200 N

Limiting friction-
fl=μsN=0.6×200=120 N

As ff(120)<F(160),
The block will begin to move and kinetic friction will act upon the block
f=fk=μkN=0.4×200=80 N

From F.B.D, along horizontal direction-
160−f=ma160−80=20a⇒a=4 m/s2

Example 5: A block of mass 40 kg slides over a surface, when a mass of 4 kg is suspended through an inextensible massless string passing over frictionless pulley as shown below. The coefficient of kinetic friction between the surface and block is 0.02 . The acceleration of block is. (Given g=10 ms−2.)

1) 1 ms−2
2) 1/5 ms−2
3) 4/5 ms−2
4) 8/11 ms−2

Solution:

flim=μN=0.02×400=8 Na=40−840+4=3244=811 m/s2

Summary

The acceleration of a block against friction involves calculating how much the block speeds up or slows down due to the opposing force of friction. This requires understanding the balance between the applied force and the frictional force, which resists motion. The net force determines the block's acceleration according to Newton's second law.