Skidding Of Vehicle On A Level Road

Skidding of a vehicle on a level road is a phenomenon that most drivers experience, often leading to sudden loss of control and potential accidents. It occurs when the tyres lose their grip on the road surface, causing the vehicle to slide uncontrollably. This can happen due to various factors such as wet or icy roads, sudden braking, or sharp turns. In real life, skidding is a common cause of accidents, particularly during adverse weather conditions. For instance, imagine driving on a rainy day when the road is slick—if you brake abruptly or turn too quickly, the vehicle may skid, making it difficult to steer and stop, leading to dangerous situations. Understanding the mechanics of skidding is crucial for drivers to avoid accidents and maintain control, especially in challenging driving conditions.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Skidding of Vehicle on a Level Road
2. Recommended Topic VideoSolved Examples Based on Skidding of Vehicles on a Level Road
3. Summary

Skidding of Vehicle on a Level Road

Skidding a vehicle on a level road is a critical issue that every driver should be aware of, as it directly impacts safety on the road. Skidding occurs when the tyres lose their traction with the road surface, leading to a loss of control. This can be triggered by factors such as sudden braking, sharp turns, or poor road conditions like rain, ice, or oil spills. In everyday life, this is a common scenario, especially during adverse weather conditions when roads become slippery. For example, driving on a wet road after a rainstorm can easily lead to skidding if proper caution isn't exercised. Understanding the causes and prevention of skidding is essential for ensuring safety and avoiding potential accidents on the road.

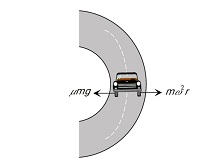
$\begin{aligned} & \text { Frictional force } \geq \text { Req. centripetal Force } \\ & \mu m g \geq \frac{m v^2}{r} \\ & V_{\text {safe }} \leq \sqrt{\mu r g} \\ & V_{\text {safe }}=\text { Safe vector move } \\ & \mathrm{r}=\text { radius of the curve } \\ & \mu=\text { coefficient of friction } \\ & V_{\text {safe }} \text { is the maximum velocity by which a vehicle can turn on a circular path of radius } \mathrm{r} \text {. }\end{aligned}$

Recommended Topic VideoSolved Examples Based on Skidding of Vehicles on a Level Road

Example 1: The coefficient of friction between tyers and road is 0.5. The maximum speed (in m/s) with which a car be driven around a curve with a radius of 20m without skidding is [ g = 10m/s²]

1) 10

2) 40

3) 15

4) 20

Solution:

Skidding of Vehicle on a Level Road

$\begin{aligned} & \text { Frictional force } \geq \text { Req. centripetal Force } \\ & \mu m g \geq \frac{m v^2}{r} \\ & V_{\text {safe }} \leq \sqrt{\mu r g} \\ & V_{\text {safe }}=\text { Safe vector move } \\ & \mathrm{r}=\text { radius of the curve } \\ & \mu=\text { coefficient of friction }\end{aligned}$

$V_{\text {safe }}$ is the maximum velocity by which a vehicle can turn on a circular path of radius r.

So,

$\begin{aligned} & \mu m g=\frac{m v_{\max }^2}{r} \\ & v_{\max }=\sqrt{\mu r g}=\sqrt{0.5 \times 20 \times 10}=10 \mathrm{~m} / \mathrm{s}\end{aligned}$

Hence, the answer is the option (1).

Example 2: A modern Grand - Prix racing car of mass m is travelling on a flat track in a circular arc of radius R with a speed v. If the coefficient of static friction between the tyres and the track is $\mu_s$, then the magnitude of negative lift $F_L$ acting downwards on the car is : (Assume forces on the four tyres are identical and g = acceleration due to gravity)

1) $-m\left(g+\frac{v^2}{\mu_s R}\right)$
2) $m\left(g-\frac{v^2}{\mu_s R}\right)$
3) $m\left(\frac{v^2}{\mu_s R}-g\right)$
4) $m\left(\frac{v^2}{\mu_s R}+g\right)$

Solution:

$\begin{aligned} & \mu_{\mathrm{s}} \mathrm{N}=\frac{\mathrm{mv}^2}{\mathrm{R}} \\ & \mathrm{N}=\frac{\mathrm{mv}^2}{\mu_{\mathrm{s}} \mathrm{R}}=\mathrm{mg}+\mathrm{F}_{\mathrm{L}} \\ & \mathrm{F}_{\mathrm{L}}=\frac{\mathrm{mv}^2}{\mu_{\mathrm{s}} \mathrm{R}}-\mathrm{mg}\end{aligned}$

Hence, the answer is the option (3).

Example 3: The maximum velocity (in ms^-1) with which a car driver must traverse a flat curve of radius 150 m and coefficient of friction 0.6 to avoid skidding is

1) 30

2) 60

3) 15

4) 25

Solution:

Skidding of Vehicle on a Level Road

Frictional force $\geq$ Req. centripetal Force
$\mu m g \geq \frac{m v^2}{r}$
$V_{\text {safe }} \leq \sqrt{\mu r g}$
$V_{\text {safe }}=_{\text {Safe vector move }}$
$r=$ radius of curve
$\mu=$ coefficient of friction
wherein
$V_{\text {safe }}$ is the maximum velocity by which a vehicle can turn on a circular path of radius r .
For no skidding along the curved track,

$
\nu=\sqrt{0.6 \times 150 \times 10}=30 \mathrm{~ms}^{-1}
$

Hence, the answer is the option (1).

Example 4: A curve in a level road has a radius of 75 m. The maximum speed of a car turning this curved road can be 30 m/s without skidding. If the radius of the curved road is changed to 48 m and the coefficient of friction between the tyres and the road remains the same, then the maximum allowed speed would be ___________m/s.

1) 24

2) 25

3) 26

4) 27

Solution:

For level road,

$\begin{aligned} & \mathrm{f}_{\mathrm{smax}}=\frac{\mathrm{mv}^2}{\mathrm{R}} \\ & \mu \mathrm{mg}=\frac{\mathrm{mv}^2}{\mathrm{R}} \\ & \mathrm{v}=\sqrt{\mu \mathrm{Rg}} \\ & \frac{\mathrm{v}_2}{\mathrm{v}_1}=\sqrt{\frac{\mathrm{R}_2}{\mathrm{R}_1}} \\ & \frac{\mathrm{v}_2}{30}=\sqrt{\frac{48}{75}} \\ & \mathrm{v}_2=24 \mathrm{~m} / \mathrm{s}\end{aligned}$

Hence, the answer is the option (1).

Example 5: A car is moving on a horizontally curved road with a radius of 50 m. The approximate maximum speed of the car will be if friction between the tyres and the road is 0.34.

[take g = 10 ms⁻²]

1) 17 ms^–1

2) 13 ms^–1

3) 22.4 ms^–1

4) 3.4 ms^–1

Solution:

$\begin{aligned} & \mu=0.34, \mathrm{R}=50 \mathrm{~m} \\ & \mathrm{~V}=\sqrt{\mu \mathrm{Rg}}=\sqrt{0.34 \times 50 \times 10}=\sqrt{34 \times 5}=\sqrt{170}=13\end{aligned}$

Hence, the answer is the option (2).

Summary

Skidding on a level road occurs when a vehicle's tyres lose traction, often due to factors like sudden braking, sharp turns, or slippery surfaces. The maximum safe speed to avoid skidding can be determined using the formula $V_{\text {safe }} \leq \sqrt{\mu r g}$ where $\mu$ is the coefficient of friction, r is the radius of the curve, and g is the acceleration due to gravity. Understanding this relationship helps in calculating the safe speed to navigate curves without skidding, ensuring safer driving conditions.