Centre Of Mass Of Hollow Cone

The centre of mass of a hollow cone is a fundamental concept in physics, especially in the study of rigid bodies. This point represents the average position of all the mass in the cone, considering its symmetrical distribution around the axis. Unlike a solid cone, the hollow nature means the mass is distributed along the surface, leading to a unique centre of mass position that is not at the geometric centre. Understanding the centre of mass is crucial in various real-life applications, such as in the design of satellite dishes, megaphones, and other conical structures where balance and stability are essential. For instance, when designing a loudspeaker horn, engineers must calculate the centre of mass to ensure that the speaker can be mounted securely without tipping, ensuring optimal sound projection.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Definition of Centre of Mass
2. Centre of Mass of Hollow Cone
3. Solved Examples Based on Centre of Mass of Hollow Cone
4. Summary

Definition of Centre of Mass

The Centre of mass of a body is defined as a single point at which the whole mass of the body or system is imagined to be concentrated and all external forces are applied there. It is the point where if a force is applied it moves in the direction of the force without rotating.

Centre of Mass of Hollow Cone

The centre of mass of a hollow cone is a critical concept in physics, particularly in mechanics, where it helps in understanding the motion and stability of objects. For a hollow cone, which has mass distributed along its surface rather than throughout its volume, the centre of mass lies along the axis of symmetry, but at a specific distance from the base that depends on the cone's dimensions.

Recommended Topic Video

Solved Examples Based on Centre of Mass of Hollow Cone

Example 1: In a hollow symmetrical cone which has symmetry about the $x$ axis and the vertex of the cone is at $(2,0,0)$ then the coordinate of the centre of mass of the mentioned hollow cone is (Height of the cone is 30 cm -1) $(2,22,0)$
2) $(20,0,0)$
3) $(0,20,0)$
4) $(22,0,0)$

Solution

Since the vertex of the cone is at $(2,0,0)$, the distance of the centre of mass of the hollow cone is at a distance of $y_{c m}=\frac{2 H}{3}$ from the vertex. So, the $y_{\mathrm{cm}}$ from the vertex is $\frac{2 H}{3}=\frac{2 \times 30}{3}=20 \mathrm{~cm}$ From the vertex Now, the x coordinate is- $20+2=22 \mathrm{~cm}$

The y and z coordinates will not change because it is symmetrical in shape.
Hence, the answer is the option (4).

Example 2: A hollow cone and a hollow semicircular shell are placed as shown in the diagram. Each has mass M . What is the y-coordinate of COM of the system

1) $\frac{10}{13} R$
2) $\frac{5}{7} R$
3) $\frac{3}{7} R$
4) $\frac{13}{12} R$

Solution

$\begin{gathered}y_{c m}=\frac{m_1 y_1+m_2 y_2}{m_1+m_2} \\ y_{c m}=\frac{\left.M\left(\frac{2 R}{3}\right)+M\left(R+\frac{R}{2}\right)\right)}{M+M} \\ y_{c m}=\frac{\left(\frac{2 M R}{3}+\left(\frac{3 M R}{2}\right)\right)}{2 M} \\ y_{c m}=\frac{13}{6} \frac{M R}{2 M} \Rightarrow y_{c m}=\frac{13}{12} R\end{gathered}$

Hence, the answer is the option (4).

Example 3: A hollow hemisphere and a hollow cone of the same mass are arranged as shown in the figure. find the position of the centre of mass from the centre of the hemisphere

1) $\frac{11}{13} R$
2) $\frac{14}{9} R$
3) $\frac{11}{12} R$
4) $\frac{5}{7} R$

Solution:

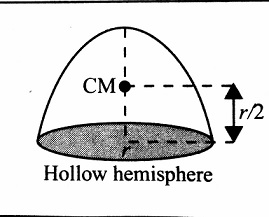
Centre of Mass of Hollow Hemisphere

It lies at a distance of $\frac{r}{2}$ from the centre of the sphere.

$\begin{aligned} & y_{c m}=\frac{m_1 y_1+m_2 y_2}{m_1+m_2} \\ & y_{c m}=\frac{M(R / 2)+M(4 R / 3)}{M+M} \\ & y_{c m}=\frac{\frac{R}{2}+\frac{4 R}{3}}{2} \\ & y_{\mathrm{cm}}=\frac{11}{12} R\end{aligned}$

Hence, the answer is the option (3).

Shown in the figure is a hollow ice cream cone (it is open at the top). If its mass is 'M', the radius of its top, R and height is H, then its M.O.I about its axis is :

1) $\frac{M H^2}{3}$
2) $\frac{M R^2}{3}$
3) $\frac{M\left(R^2+H^2\right)}{4}$
4) $\frac{M R^2}{2}$m

Solution:

We will take an elemental ring of thickness dy and radius r at a slant height y as shown in the figure
$
\begin{aligned}
& \text { given, Mass }=M \\
& \text { Radius }=R \\
& I_{H C}=\int d I \text { ring }=\int(d m) r^2 \\
& d m=\frac{M}{\pi R l}(2 \pi r d y)
\end{aligned}
$

where dm is the mass of the elemental ring

$
\begin{aligned}
& I_{H C}=\int \frac{2 M}{R \ell} r^3 d y \\
& \frac{r}{R}=\frac{y}{l} \quad \Rightarrow \quad r=\frac{R}{l} y \\
& I_{H C}=\frac{2 M}{R l} \frac{R^3}{l^3} \int_0^l y^3 d y=\frac{M R^2}{2}
\end{aligned}
$

Hence, the answer is the option (4).

Summary

The centre of mass of a hollow cone, an essential concept in physics, lies along its axis of symmetry at a specific distance from the base. This understanding is crucial in analyzing the stability and motion of objects, especially in real-life applications like the design of satellite dishes, megaphones, and other conical structures. It ensures balance and stability, particularly in engineering and construction, where precise calculations are necessary to prevent tipping and optimize functionality.