Rolling Without Slipping
Rolling without slipping is a common phenomenon we encounter in our daily lives. It occurs when an object, like a wheel or a ball, rolls along a surface without sliding. This means that at any instant, the point of the object in contact with the ground is momentarily at rest relative to the ground. Think of a bicycle tire on the road; as it rolls, the point where the tire touches the road isn’t skidding but gripping the surface perfectly. This concept is crucial for understanding how vehicles move efficiently and how energy is conserved in rolling motions. It also plays a key role in various sports, like bowling, where the ball needs to roll smoothly down the lane. Let's read this concept in this article with some solved examples to boost your confidence.
This Story also Contains
- The Linear Velocity of Different Points
- Solved Examples Based on Rolling Without Slipping
- Summary
The Linear Velocity of Different Points
- In pure Translation: All points of a rigid body have the same linear velocity.

- In pure Rotation: All points of a rigid body have the same angular speed but different linear velocities depending on their distance from the axis of rotation.

And in Rolling all points of a rigid body have the same angular speed ($\omega$) but different linear speeds.
I.e 
During Rolling motion
$\begin{aligned} & \text { If } V_{c m}>R w \rightarrow \text { slipping motion } \\ & \text { If } V_{c m}=R w \rightarrow \text { pure rolling } \\ & \text { If } V_{c m}<R w \rightarrow \text { skidding motion }\end{aligned}$
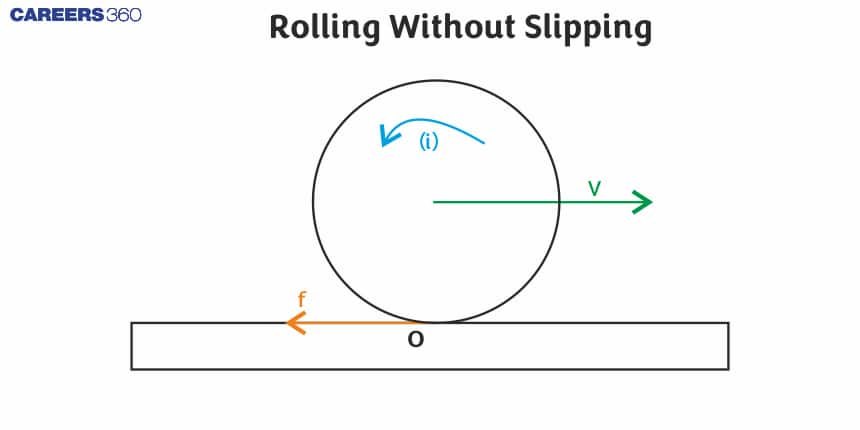
When the object rolls across a surface such that there is no relative motion of the object and surface at the point of contact, the motion is called rolling without slipping.

Here the point of contact is P.
Friction force is available between object and surface but work done by it is zero because there is no relative motion between body and surface at the point of contact.
Or we can say No dissipation of energy is there due to friction.
I.e., Energy is conserved.
Which is $K_{\text {net }}=K_T+K_R=\frac{1}{2} m V^2+\frac{1}{2} I \omega^2$
Now using $V=\omega \cdot R$
And using $K_{\text {net }}=\frac{1}{2} m V^2+\frac{1}{2} I \omega^2=\frac{1}{2}\left(I+m R^2\right) \omega^2$
Where I = moment of inertia of the rolling body about its centre ‘O’
And using the Parallel axis theorem
We can write $I_p=I+m R^2$
So we can write $K_{\text {net }}=\frac{1}{2} I_p \omega^2$
Where $I_p$ =moment of inertia of the rolling body about point of contact ‘P’.
So this Rolling motion of a body is equivalent to a pure rotation about an axis passing through the point of contact (here through P) with the same angular velocity $\omega$.
Here, the axis passing through the point of contact P is also known as the Instantaneous axis of rotation.
(Instantaneous axis of rotation-Motion of an object may look as pure rotation about a point that has zero velocity.)
Net Kinetic Energy for different rolling bodies
${ }_{\mathrm{As}} K_{\text {net }}=K_T+K_R=\frac{1}{2} m V^2\left(1+\frac{K^2}{R^2}\right)$
So the quantity $\frac{K^2}{R^2}$ will have different values for different bodies.
| Rolling body | $\frac{K^2}{R^2}$ | $K_{\text {net }}$ |
Ring Or Cylindrical shell | 1 | $m V^2$ |
Disc Or solid cylinder | 1/2 | $\frac{3}{4} m V^2$ |
| Solid sphere | 2/5 | $\frac{7}{10} m V^2$ |
| Hollow sphere | 2/3 | $\frac{5}{6} m V^2$ |
The direction of friction
Kinetic friction will always oppose the rolling motion. While Static friction on the other hand only opposes the tendency of an object to move.
When an external force is in the upward diametric part
- If $K^2=R x$ then no friction will act
- If $K^2>R x$ then Friction will act in the backward direction
- If $K^2<R x$ then Friction will act in a forward direction
If an external force is in the lower diametric part, Then friction always acts backwards.
Recommended Topic Video
Solved Examples Based on Rolling Without Slipping
Example 1: A string is wound around a hollow cylinder of mass 5 kg and radius 0.5m. If the string is now pulled with a horizontal force of 40N, and the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration ( in rad/s2 ) of the cylinder will be (neglect the mass and thickness of the string):
1) 20
2) 16
3) 12
4) 10
Solution:
Draw FBD of the hollow cylinder

It is rolling without slipping.
So the point of contact of the ground & hollow cylinder will be at rest.
$
\begin{aligned}
& \text { So } a=R \alpha \cdots(1) \\
& \text { apply } \sum F_x=m a_x \\
& \Rightarrow 40+f=m a=m R \alpha \cdots \text { (2) } \\
& \text { apply } \tau=I \alpha \quad \text { (about } 0 \text { point) } \\
& 40 \times R-f \times R=m R^2 \alpha \cdots \text { (3) }
\end{aligned}
$
From (2) \& (3)
$
\alpha=\frac{40}{M R}=16 \mathrm{rad} / \mathrm{s}^2
$
Hence, the answer is option (2).
Example 2: A solid sphere and cylinder of identical radii and mass approach an incline with the same liner velocity (see figure ). Both roll without slipping all throughout. The two climb maximum heights $h_{\text {sph }}$ and $h_{\text {cyl }}$ on the incline. The ratio $\frac{h_{\text {sph }}}{h_{\text {cyl }}}$ is given by:

1) $\frac{2}{\sqrt{5}}$
2) 1
3) $\frac{14}{15}$
4) $\frac{4}{5}$
Solution:
$
V=w R
$
For sphere
$
\begin{aligned}
m g h_1 & =k_1=\frac{1}{2} I w^2+\frac{1}{2} m v^2 \\
& =\frac{1}{2} \times \frac{2}{5} m R^2 w^2+\frac{1}{2} m v^2 \\
& =\left(\frac{1}{5}+\frac{1}{2}\right) m v^2=\frac{7}{10} m v^2
\end{aligned}
$
For solid cylinder
$
\begin{aligned}
& m g h_2=k_2=\frac{1}{2} m v^2+\frac{1}{2} \frac{m R^2}{2} w^2=m v^2\left(\frac{1}{2}+\frac{1}{4}\right)=\frac{3}{4} m v^2 \\
& \frac{m g h_1}{m g h_2}=\frac{k_1}{k_2}=\frac{\frac{7}{10} m v^2}{\frac{3}{4} m v^2}=\frac{28}{30}=\frac{14}{15}
\end{aligned}
$
Hence, the answer is option (3).
Example 3: The following bodies are made to roll up (without slipping) the same inclined plane from a horizontal plane :(i) a ring of radius R , (II) a solid cylinder of radius $\frac{R}{2}$ and (iii) a solid sphere of radius $\frac{R}{4}$, If in each case, the speed of the centre of mass at the bottom of the incline is the same, the ratio of the maximum heights they climb is :
1) $4: 3: 2$
2) $20: 15: 14$
3) $14: 15: 21$
4) $2: 3: 4$
Solution:
$\frac{1}{2} m v_0^2=$ Translational kinetic energy of the centre of mass
$\frac{1}{2} I_{c m} w^2=$ Rotational kinetic energy about the centre of mass
$h=\frac{\left(1+\frac{K^2}{R^2}\right) V^2}{2 g}$ using the values of $\frac{K^2}{R^2}$ for given bodies, where K is the radius of
gyration
$
=h_1: h_2: h_3=20: 15: 14
$
Hence, the answer is the option (2).
Example 4: A solid spherical ball is rolling on a frictionless horizontal plane surface about its axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is -
1) $\frac{2}{5}$
2) $\frac{2}{7}$
3) $\frac{1}{5}$
4) $\frac{7}{10}$
Solution:
For solid spherical ball -
$
\mathrm{I}=\frac{2}{5} \mathrm{mr}^2
$
Rotational kinetic energy is given by
$
\begin{aligned}
& \mathrm{KE}_{\mathrm{R}}=\frac{1}{2} \mathrm{I} \omega^2 \\
& =\frac{1}{2} \times\left(\frac{2}{5} \mathrm{mr}^2\right) \frac{\mathrm{v}^2}{\mathrm{r}^2} \\
& =\frac{2}{5}\left(\frac{1}{2} m v^2\right) \\
& \mathrm{KE}_{\mathrm{R}}=\frac{2}{5} \mathrm{KE}_{\mathrm{T}} \\
&
\end{aligned}
$
Here,
$\mathrm{KE}_{\mathrm{T}}$ is the translational kinetic energy
$
\begin{aligned}
\mathrm{KE}_{\text {total }} & =\mathrm{KE}_{\mathrm{R}}+\mathrm{KE}_{\mathrm{T}} \\
& =\frac{7}{5} \mathrm{KE}_{\mathrm{T}} \\
\frac{\mathrm{KE}_{\mathrm{R}}}{\mathrm{KE}_{\text {total }}} & =\frac{2}{7}
\end{aligned}
$
Hence, the answer is the option (2).
Example 5: A uniform disc with mass $M=4 \mathrm{~kg}$ and radius $\mathrm{R}=10 \mathrm{~cm}$ is mounted on a fixed horizontal axle as shown in the figure. A block with mass $\mathrm{m}=2 \mathrm{~kg}$ hangs from a massless cord that is wrapped around the rim of the disc. During the fall of the block, the cord does not slip and there is no friction at the axle. The tension in the cord is $\qquad$ N.
$\left(\right.$ Take $\mathrm{g}=10 \mathrm{~ms}^{-2}$ )

1) 10
2) 20
3) 30
4) 40
Solution:
$
\begin{aligned}
& R=0.1 \mathrm{~m} \\
& I=\frac{M R^2}{2}=0.02 \\
& 20-T=2 a-(1) \\
& T \times 0.1=0.02 \times \alpha=0.02 \times \frac{a}{0.1}-(2) \\
& \Rightarrow T=2 a, a=5 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$
So, $T=10 \mathrm{~N}$
Hence, the answer is option (1).
Summary
Combining translational and rotational motion results in pure rolling. In a pure rolling state, the body is not affected by the friction force. Consequently, regardless of how rough the surface is, there should ideally be no energy loss via friction. This is a significant rolling property. Since rolling motion loses the least amount of energy, machines with rounded wheels and ball bearings utilise less energy. Pure rolling is a crucial idea in rigid body dynamics with a wide range of applications.

