Coefficient Of Friction Between A Body And Wedge

The coefficient of friction between a body and a wedge plays a crucial role in determining the ease with which the body can slide over the wedge's surface. This fundamental concept in physics helps us understand the interaction between surfaces in contact. In real life, we encounter such interactions in various scenarios, from moving furniture across a floor to driving a car on a ramp. Understanding the coefficient of friction can aid in designing safer and more efficient systems in everyday applications, ensuring stability and preventing unwanted slippage. This article explains into the principles behind the coefficient of friction, its calculation, and its practical implications.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

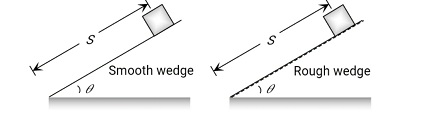
1. Case 1- A body Slides on a Smooth Wedge of Angle θ and its Time of Descent is t.
2. For smooth wedge
3. Case 2- If the Same Wedge is Made Rough Then the Time Taken by it to Come Down becomes n times more (i.e., nt)
4. Solved Example Based on Coefficient Of Friction Between A Body And Wedge
5. Summary

Case 1- A body Slides on a Smooth Wedge of Angle θ and its Time of Descent is t.

For smooth wedge

S=u⋅t+12at2S=12(gsin⁡θ)t2....(i)u=0a=gsin⁡θ

Case 2- If the Same Wedge is Made Rough Then the Time Taken by it to Come Down becomes n times more (i.e., nt)

For Rough wedge

S=12g[sin⁡θ−μcos⁡θ](nt)2 (i) = (ii) μ=tan⁡θ[1−1n2]

μ= coefficient of friction θ= Angle of inclination n= an integer

Recommended Topic Video

Solved Example Based on Coefficient Of Friction Between A Body And Wedge

Example 1: A body takes just twice the time as long to slide down a plane inclined at 30⁰ to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is:

1) 34
2) 3
3) 43
4) 34

Solution:

Coefficient of Friction Between a Body and Wedge -

If the same wedge is made rough then the time taken by it to come down becomes n times more (nt)

Then find the Coefficient of Friction between the body and wedge in terms of n.

For this make 2 cases

Case 1- A body slides on a smooth wedge of angle θ and its time of descent is t.

Case 2- If the same wedge is made rough then the time taken by it to come down becomes n times more (i.e., nt)

(The length of the path in both cases are the same)

For smooth wedge

S=u⋅t+12at2S=12(gsin⁡θ)t2....(i)u=0a=gsin⁡θ

For Rough wedge

S=12g[sin⁡θ−μcos⁡θ](nt)2...(ii) (i) = (ii) μ=tan⁡θ[1−1n2]

μ= coefficient of friction θ= Angle of inclination n= an integer

By using this concept -

μ=tan⁡Θ(1−1n2)=tan⁡30(1−122)=34

Hence, the answer is option (1).

Example 2: In case (i) plane is smooth and in case (ii) plane is rough. If the time taken by the block in case (ii) to come down is 3 times to the time to come down in case (i) then the coefficient of friction of plane in case (ii) is?

1) 13
2) 23
3) 34
4) 12

Solution:

Length covered in both cases is same so for smooth wedge s=ut+12at2

s1=12at2s1=12gsin⁡θt2−(I)[a=gsin⁡θ]

For rough wedge
s2=12g(sin⁡θ−μcos⁡θ)(nt)2−(II)[a=g(sin⁡θ−μcos⁡θ)]

Now s1=s2
12gsin⁡θt2=12g(sin⁡θ−μcos⁡θ)(nt)2

Solving

μ=tan⁡θ[1−1n2]=34[1−132]=34×89⇒23

Hence, the answer is option (2).

Example 3: A sphere of radius R is in contact with a wedge. The point of R contact is R/3 from the ground as shown in the figure. Wedge is moving with a velocity 10 m/s, then the velocity of the sphere at this instant will be:

1) 10 m/s
2) 33 m/s
3) 55 m/s
4) 15 m/s

Solution:

By wedge constraint,

Relative velocity along the line perpendicular to the contact surface is zero.

10sin⁡θ=Vcos⁡θ10tan⁡θ=VV=10×52=55 m/s

Hence, the answer is option (3).

Summary

This article explores the concept of the coefficient of friction between a body and a wedge, examining its impact on the interaction between surfaces and motion. The coefficient of friction, which depends on the materials in contact, represents the portion of the force of friction holding between surfaces. The article elaborates on how this coefficient significantly influences the stability and ease of movement on inclined planes.