Conservation of Mechanical Energy - Definition, Example, Formula, FAQs

Edited By Vishal kumar | Updated on Sep 24, 2024 10:08 PM IST

In this article, we are going to learn about mechanical energy and types of mechanical energy. We will learn what is mechanical energy or the mechanical energy definition, what are the two forms of mechanical energy and also state the law of conservation of mechanical energy. The mechanical energy meaning is , the energy of a body due to which the body gets ability to do work for its motion or speed. By discussing some mechanical energy example we will learn how it exist in this physical world.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

Conservation of Mechanical Energy - Definition, Example, Formula, FAQs

Mechanical Energy:

The sum of kinetic energy and potential energy of a body, is known as mechanical energy of a body .

Example of mechanical energy –

A ball kept on the top of a building at rest ,that is potential energy .After some time the ball is freely falling downward, this is kinetic energy .

Example of mechanical energy:

Q. Kinetic energy of an object is 12 J and potential energy 8 J, what is the mechanical energy of the object ?

Ans: kinetic energy = 12 J

Potential energy = 8 J

Total mechanical energy of the object = 12 + 8 = 20 J

Also read -

Mechanical Power:

The rate of doing mechanical work with respect to time is known as mechanical power.

Law of conservation of mechanical energy or principle of conservation of mechanical energy:

The law of conservation of mechanical energy states that, in an isolated system or if there is no energy dissipation, then the total mechanical energy of the system remains constant.

Conservation of mechanical energy formula:

Mechanical energy = Kinetic energy + potential energy

Example for conservation of mechanical energy:

If a ball of mass m is dropped from height h , initially is was at rest at that height. When it is falling freely the potential energy gets converted into the kinetic energy in the motion.

Types of mechanical energy:

There are two types of mechanical energy.

Kinetic energy
Potential energy

Kinetic energy:

The mechanical energy of a body due to its motion is known as kinetic energy. The working power of a body due to its motion can also be called kinetic energy .

Also read :

Example of kinetic energy:

A ball is moving with a velocity
A freely falling body
A bullet is fired from a gun towards the target

Mathematical formula of kinetic energy:

Kinetic Energy= 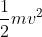$\frac{1}{2}mv^2$

Where, m is the mass and v is the velocity of the object .

Example problem :

Q. A ball of mass 50 kg is moving with a velocity 5 m/s , what is its kinetic energy ?

Ans: mass of the ball , m = 50 Kg

velocity , v = 5 m/s

kinetic energy of the ball =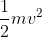 $\frac{1}{2}mv^2$

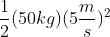
= $\frac{1}{2}(50kg)(5\frac{m}{s})^2$

=125 J

Potential energy:

The mechanical energy of a body due to its position is known as potential energy. The working power of a body due to its position or configuration can also be called potential energy.

Example of potential energy:

A ball is kept in rest at a height
A box is kept in rest at an incline plane (friction less)

Related Topics Link,

Mathematical formula of potential energy:

potential energy=mgh

Where, m is the mass of a body, h is the height from the ground where the object is kept, g is the gravitational acceleration.

Example problem:

Q. A ball of mass 50 kg is kept at height 15 m above the ground, what is its potential energy?

Ans: mass of the ball , m = 50 Kg

height, h = 15 m

gravitational acceleration, g = 9.8 m/s²

Potential energy of the ball = mgh

= (50 Kg)×(9.8 m/s²)×(15 m)

= 7350 J

NCERT Physics Notes :

There are few more types of potential energy:

Elastic potential energy
Gravitational potential energy

Elastic Potential energy in a spring:

The energy which is generated due to application of force .When the external force is applied to the elastic object then the elastic potential energy stays stored until the objects comes to its equilibrium position.

Example: when a spring of spring constant k is displaced from x (equilibrium position) to y position , then the potential energy of the spring will be, 1 / 2 k(y-x)²

Gravitational potential energy:

The potential energy of a body when it is kept at height from the earth’s surface, it is known as gravitational potential energy of that body.

Example: If the mass of an object is m , height from the earth’s surface is h and gravitational acceleration is g ,therefore the gravitational potential energy of the object will be mgh .

The sign of gravitational potential energy is negative (‘-‘).

When a body is lifted upwards from the earth’s surface the displacement of the body is in the opposite direction of the earth’s surface. As the displacement's direction is negative , the total gravitational potential energy becomes negative.

Also check-

Frequently Asked Questions (FAQs)

1. What is mechanical energy?

The sum of kinetic energy and potential energy of a body is called mechanical energy of a body.

2. What is the S.I unit of mechanical energy?

The S.I unit of mechanical energy is Joule.

3. What is conservative system?

When the total mechanical energy of a system is conserved , then that system is called conservative system. The force acting on such systems is known as conservative force.

4. Give some examples of conservative forces.

Gravitational force , electrostatic force, magnetic force between two poles etc.

5. What is non-conservative force?

In a system where resistive forces are present and mechanical energy of that system is not conserved, such a system is called non-conservative system. The resistive force is known as non-conservative force.

Example of a non-conservative force is frictional force .