Work Done By A Constant Force: Definition, Formula, Examples, Questions

Work Done By A Constant Force

Edited By Vishal kumar | Updated on Sep 25, 2024 04:17 PM IST

Work is considered to be done when a force operating on a body can really move it a certain distance in the direction of the force. The watchman at the office gate is not causing any load to move and is simply standing there, thus both force and displacement are zero. Similarly, no work is done by the watchman. When the coolie bears a load on his head, he applies vertical effort to support it. With the load on his head, the coolie moves horizontally along the platform. Since no distance is covered along the vertical, that is, in the direction of the force exerted by him, the work performed by the coolie is also zero.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Define Work
Dependence Of Work Done By A Constant Force
Types of Work
Solved Examples Based on Work Done By a Constant Force
Summary

Work Done By A Constant Force

In this article, we will cover the concept of work and its types, including work done by a constant force. This concept falls under the broader category of work, energy, and power, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept, including two in 2019, one in 2020, two in 2021, and one in 2023. And for NEET two questions were asked from this concept.

Let's read this entire article to gain an in-depth understanding of the work done by a constant force.

Define Work

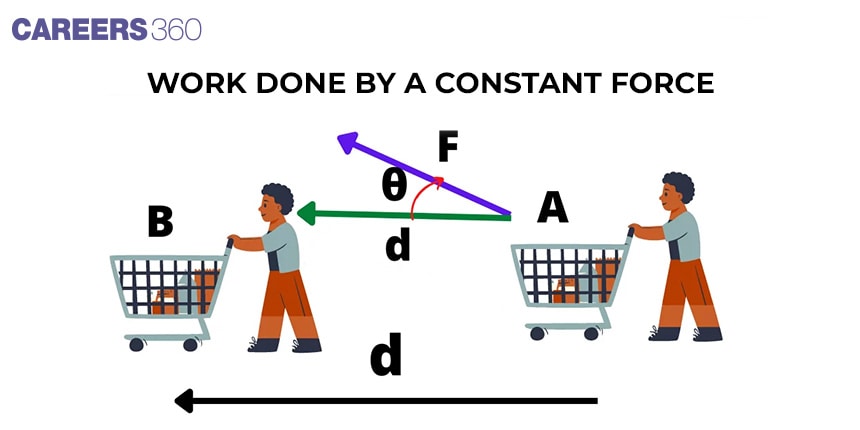
Work is said to be done when a force applied on the body displaces the body through a certain distance along the direction of the force.

Work Done By a Constant Force

1. The scalar product of the force vector $(\vec{F})$ and the displacement vector $(\vec{S})$
$W = \vec{F} \cdot \vec{S}$
2. The product of the magnitude of force $(F)$ magnitude of displacement $(S)$ and cosine of the angle between them $(Θ)$
$W = F S \cos Θ$
3. If the number of forces $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}} \dots \dots, {\vec{F}}_{n}$ , are acting on a body and it shifts from position vector $\vec{r_{1}}$ to position vector $\vec{r_{2}}$
$Then W = ({\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} \dots \dots \dots + {\vec{F}}_{n}) \cdot ({\vec{r}}_{2} - {\vec{r}}_{1}) = {\vec{F}}_{n e t} \cdot {\vec{r}}_{n e t}$
4. Units-
SI Unit-Joule
CGS Unit- Erg
1 Joule $= 10^{7} Erg$
5. Dimension- $M L^{2} T^{- 2}$

1. The scalar product of the force vector $(\vec{F}$ ) and the displacement vector ( $\vec{S}$ )
$W = \vec{F} \cdot \vec{S}$
2. The product of the magnitude of force $(F)$ magnitude of displacement $(S)$ and cosine of the angle between them $(Θ)$
$W = F S \cos Θ$
3. If the number of forces ${\vec{F}}_{1}, {\vec{F}}_{2}, {\vec{F}}_{3} \dots \dots, {\vec{F}}_{n}$ , are acting on a body and it shifts from position vector $\vec{r_{1}}$ to position vector $\vec{r_{2}}$
Then
$W = ({\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} \dots \dots . + {\vec{F}}_{n}) \cdot ({\vec{r}}_{2} - {\vec{r}}_{1}) = {\vec{F}}_{n e t} \cdot {\vec{r}}_{n e t}$

4. Units-
- SI Unit-Joule
- CGS Unit- Erg
- 1 Joule $= 10^{7} E r g$
5. Dimension- $M L^{2} T^{- 2}$

Dependence Of Work Done By A Constant Force

Till now we have studied the work and work done by a constant force now we are going to study the dependence of work done by a constant force, in which mainly covers the frame of reference.

- Frame of reference: With a change of frame of reference (inertial), force does not change while displacement may change. So the work done by a force will be different in different frames. i.e. A person is pushing a box inside a moving train with a force $\vec{F}$ , displacement inside train $\vec{S}$ and displacement of the train in the ground frame is ${\vec{S}}_{0}$

Then work done by $W = \vec{F} \cdot (\vec{S} + {\vec{S}}_{0})$

Types of Work

There are mainly three types of work which are mentioned below:

Positive Work-

Positive work means that force (or its component) is parallel to displacement.
Means $0 \leq Θ < \frac{π}{2}$

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Where $Θ$ is the angle between force vectors and displacement vector

Maximum work $= W_{max} = F S$ , When $θ = 0^{0}$
E.g When you move a block by pulling it then work done by you on the block is positive

Negative Work

Negative work means that force (or its component) is opposite to displacement.
Means $\frac{π}{2} < Θ \leq π$

Where $\Theta$ is the angle between force vectors and displacement vector

Minimum work= $W_{min} = - F S$ , When $θ = 180^{\circ}$
E.g When a body is made to slide over a rough surface, the work done by the frictional force is negative

Zero work

Under three conditions Work can be zero

a. If the force is perpendicular to the displacement

Means $Θ = \frac{π}{2}$

E.g-When a body moves in a circle the work done by the centripetal force is always zero.

b. If there is no displacement (means s = 0)

E.g- When a person tries to displace a wall by applying a force and can't able to move the wall

So the work done by the person on the wall is zero.

c. If there is no force acting on the body (means F=0)

E.g- Motion of an isolated body in free space.

Solved Examples Based on Work Done By a Constant Force

Example 1: A force $\vec{F} = 5 \hat{i} - 4 \hat{j} + \hat{k}$ moves a body of mass 10 Kg from position (3,4,5) to position (6,7,8). Find the work (Joule) done :

Solution:

The scalar product of the force vector $(\vec{F})$ and the displacement vector $(\vec{S})$
$\begin{aligned} w = \vec{F} \cdot \vec{S} \\ \vec{s_{1}} = 3 \hat{i} + 4 \hat{j} + 5 \hat{k} \\ \vec{s_{2}} = 6 \hat{i} + 7 \hat{j} + 8 \hat{k} \\ \vec{S} = \vec{s_{2}} - \vec{s_{1}} = 3 \hat{i} + 3 \hat{j} + 3 \hat{k} \\ w = \vec{F} \cdot \vec{s} = (5 \hat{i} - 4 \hat{j} + \hat{k}) \cdot (3 \hat{i} + 3 \hat{j} + 3 \hat{k}) = 15 - 12 + 3 = 6 J \end{aligned}$

Hence, the answer is the option (4).

Example 2: A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle, the motion of the particle takes place in a plane. It follows that :

its velocity is constant

its acceleration is constant

its kinetic energy is constant (correct)

it moves in a straight line.

Solution:

Net work done by all the forces gives the change in kinetic energy -

$\begin{aligned} W = \frac{1}{2} m v^{2} - \frac{1}{2} m v_{0}^{2} \\ W = k_{f} - k_{i} \\ - wherein \\ m = mass of the body \\ v_{0} = initial velocity \\ v = final velocity \end{aligned}$
- wherein
$m =$ mass of the body
$v_{0} =$ initial velocity
$v =$ final velocity
As $w = \vec{F} \cdot \vec{S}$ or
$W = \int \vec{F} \cdot \vec{v} d t$

In this case, since force is constant and it is always perpendicular to velocity, the work done by this force is zero. Hence kinetic energy remains constant.

Hence, the correct answer is option(3)

Example 3: A block of mass m is kept on a platform which starts from rest with constant acceleration g/2 upward, as shown in the figure. Work done by the normal reaction on the block in time t is:

1. $- \frac{m g^{2} t^{2}}{8}$
2. $\frac{m g^{2} t^{2}}{8}$
3. 0
4) $\frac{3 m g^{2} t^{2}}{8}$

Solution:

The scalar product of the force vector $(\vec{F})$ and the displacement vector $(\vec{S})$
By balancing the forces in the vertical direction, we get:
$\Rightarrow N - M g = \frac{M g}{2} \Rightarrow N = \frac{3 m g}{2}$
and displacement is given by the equation:
$s = u t + \frac{1}{2} a t^{2}$
where $u = 0$ and $a = g / 2$
$\Rightarrow \vec{S} = \frac{1}{2} \frac{\vec{g}}{2} t^{2}$
and we know,
$\begin{aligned} W_{N} = \vec{N} \cdot \vec{S} \\ \Rightarrow W = \frac{3 m g^{2} t^{2}}{8} \end{aligned}$

Example 4: A particle which is experiencing a force, given by $\vec{F} = 3 \vec{i} - 12 \vec{j},$ undergoes a displacement of $\vec{d} = 4 \vec{i}$ . If the particle had a kinetic energy of 3J at the beginning of the displacement, What is its kinetic energy (in Joule) at the end of the displacement?

Solution:

Net work done by all the forces gives the change in kinetic energy -

$\begin{aligned} W = \frac{1}{2} m v^{2} - \frac{1}{2} m v_{0}^{2} \\ W = k_{f} - k_{i} \\ - wherein \\ m = mass of the body \\ v_{0} = initial velocity \\ v = final velocity \\ W = F . d = 3 \times 4 = 12 J \\ W_{net} = Δ K E \\ 12 = Kf - 3 \\ Kf = 15 J \end{aligned}$

Hence, the answer is the option (3).

Example 5: A lift of mass m is moving in an upward direction with acceleration g/4 , its displacement is 'h'. Find out work (in mgh) done by the tension force

1) 0.25

2) 1.25

3) 2

4) 0.75

Solution:

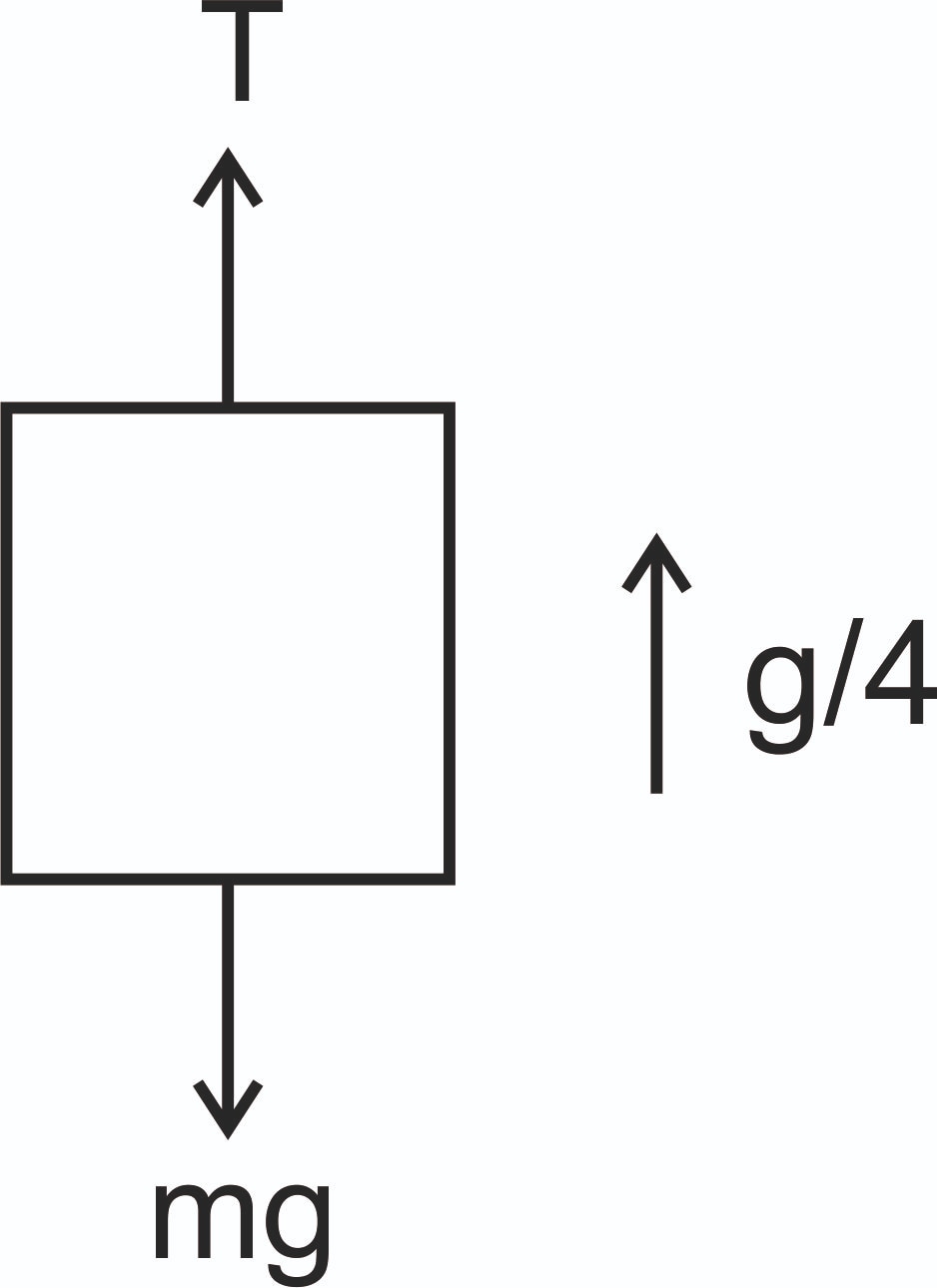
1722492902676

$\begin{aligned} T - mg = m (g / 4) \\ T = 5 / 4 mg \\ W = F S \cos θ \\ W = [5 / 4 mg] h \cos θ \\ W = 5 / 4 mgh \end{aligned}$

Hence, the answer is option (2).

Summary

If nothing is actually moving, no work is done- no matter how great the force is involved. Work is a scalar quantity but you can have positive and negative work. positive work is where the force pulls in the same direction as the movement. Negative work is where the force is in the opposite direction. This is the very first concept of work energy and power after this we generally study the Work Done By Variable Force.