Davisson-Germer Experiment

The Davisson-Germer experiment, conducted in 1927 by American physicists Clinton Davisson and Lester Germer, was a landmark study that provided crucial evidence for the wave-particle duality of matter. By demonstrating the diffraction of electrons off a nickel crystal, this experiment confirmed that electrons exhibit wave-like behaviour, a foundational concept in quantum mechanics. This discovery has profound implications in real-life applications, such as the development of electron microscopes, which rely on electron diffraction to achieve high-resolution imaging. Understanding wave-particle duality is essential for innovations in materials science, nanotechnology, and the broader field of quantum physics. In this article, we will delve into the details of the Davisson-Germer experiment and its significance in modern science.

This Story also Contains

1. Davisson-Germer Experiment
2. Galvanometer in Davisson Germer Experiment
3. Frank Hertz Experiment
4. Solved Examples Based on the Davisson-Germer Experiment
5. Summary

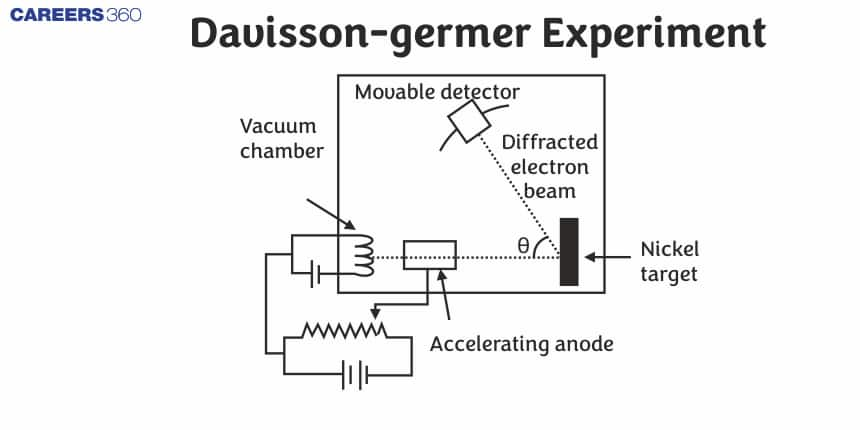
Davisson-Germer Experiment

The Davisson-Germer experiment, conducted in 1927 by American physicists Clinton Davisson and Lester Germer, was a groundbreaking study that provided direct evidence for the wave nature of electrons, a key concept in quantum mechanics. The experiment involved directing a beam of electrons at a nickel crystal and observing the resulting diffraction pattern, which resembled the pattern produced by X-rays or light waves when they encountered a similar obstacle. This finding confirmed Louis de Broglie's hypothesis that particles of matter, such as electrons, exhibit both wave-like and particle-like properties. Davisson and Germer's experiment, for the first time, proved the wave nature of electrons through electron diffraction and verified the de Broglie equation. In this experiment, we will study the scattering of electrons by a Ni crystal.

The experimental setup for the Davisson and Germer experiment is enclosed within a vacuum chamber.

The experimental arrangement of the Davisson Germer experiment consists of the following main parts

Electron Gun

An electron gun comprising of a tungsten filament F was coated with barium oxide and heated through a low-voltage power supply. It emits electrons when heated to a particular temperature. The electrons emitted by the electron gun are again accelerated to a particular velocity.

Collimator

The accelerator is enclosed within a cylinder perforated with fine holes along its axis, these emitted electrons were made to pass through it. Its function is to render a narrow and straight (collimated) beam of electrons ready for acceleration.

Target

The target is a Nickel crystal. The beam produced from the cylinder is again made to fall on the surface of a nickel crystal. The crystal is placed such that it can be rotated about a fixed axis. Due to this, the electrons scatter in various directions.

Detector

A detector is used to capture the scattered electrons from the Ni crystal. The beam of electrons produced has a certain amount of intensity which is measured by the electron detector and after it is connected to a sensitive galvanometer, it is then moved on a circular scale to record the current.

Observations of the Davisson Germer Experiment

• The intensity of the scattered electron beam is measured for different values of the angle of scattering by changing the $\phi$ (angle between the incident and the scattered electron beams).

These electrons formed a diffraction pattern. Thus the dual nature of matter was verified.

• The energy of the incident beam of electrons can be varied by changing the applied voltage to the electron gun.

Note-Intensity of a scattered beam of electrons is found to be maximum when the angle of scattering is $50^{\circ}$ and the accelerating potential is 54 V.

i.e. we could see a strong peak in the intensity. This peak was the result of the constructive interference of the scattered electrons.

The intensity of the scattered electrons is not continuous. It shows a maximum and a minimum value corresponding to the maxima and the minima of a diffraction pattern produced by X-rays.

Galvanometer in Davisson Germer Experiment

In the Davisson-Germer experiment, the galvanometer played a crucial role in detecting and measuring the intensity of the electrons scattered by the nickel crystal.

The detector is connected to a sensitive galvanometer to measure the small values of current due to a scattered beam of electrons.

Bragg’s Formula

Bragg's formula, also known as Bragg's law, is a fundamental equation in the field of X-ray crystallography. It relates the angles at which X-rays are diffracted by the atomic planes in a crystal to the wavelength of the X-rays and the distance between the planes.

The path difference between electrons scattered from adjacent crystal planes is given by $\Delta x=2 d \sin \theta$

and For constructive interference between the two scattered beams

$\Delta x=2 d \sin \Theta=n \lambda$

where $d$ - the distance between dif fracting planes
and $\theta$ is the angle between the incident rays and the surface of the crystal

For the above figure $\phi=$ scattering angle
As $\theta+\phi+\theta=180^{\circ}$
So $\Theta=\frac{180-\phi}{2}$

The intensity of a scattered beam of electrons is found to be maximum when the angle of scattering is $50^{\circ}$

So For $\phi=50^{\circ}$ we get $\theta+50^{\circ}+\theta=180^{\circ}$ we get $\theta=65^{\circ}$

Co-relating Davisson Germer experiment and de Broglie relation

According to de Broglie

$\lambda_e=\frac{12.27}{\sqrt{V}} A^{\circ}$

and using V = 54 Volt we get $\lambda_e=0.167 \mathrm{~nm}$

From Bragg’s formula, we have $2 d \sin \Theta=n \lambda$

The Lattice Spacing in Ni Crystal is given as d=0.092 nm.

And using $n=1, \phi=50^{\circ}$ and $V=50$ Volt

we get $\lambda_e=0.165 \mathrm{~nm}$

Therefore the experimental results are in close agreement with the theoretical values obtained from the de Broglie equation.

Thus Davisson and Germer's Experiment verify the de Broglie equation.

Frank Hertz Experiment

The Frank-Hertz experiment, conducted by James Franck and Gustav Hertz in 1914, was a pivotal experiment in the development of quantum physics. It provided direct evidence for the existence of quantized energy levels in atoms, supporting Niels Bohr's model of the atom. In this experiment, electrons were accelerated through a gas of mercury atoms, and the energy exchange between the electrons and the mercury atoms was studied. This experiment is the first experimental verification of the existence of discrete energy states in atoms. For this experiment, the graph of Collected current vs. accelerating Voltage is given below

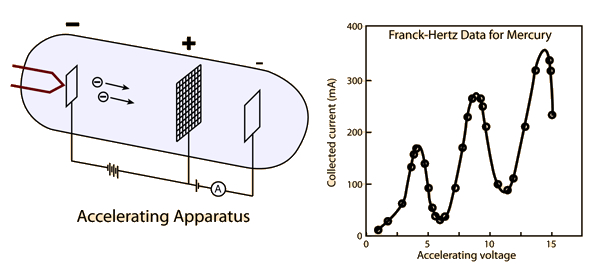
Frank and Hertz proposed that the 4.9 V characteristic of their experiments was due to the ionization of mercury atoms by collisions with the flying electrons emitted at the cathode.

Solved Examples Based on the Davisson-Germer Experiment

Example 1: This question has statement 1 and statement 2 of the four choices given after the statements, choose the one that best describes the two statements

statement 1: Davisson – Germer experiment established the wave nature of electrons.

statement 2: If electrons have a wave nature, they can interfere and show diffraction.

1) Statement 1 is false, Statement 2 is true

2) Statement 1 is true, Statement 2 is false

3) Statement 1 is true, Statement 2 is true and the correct explanation for statement 1

4) Statement 1 is true, Statement 2 is true, and Statement 2 is not the correct explanation for statement 1.

Solution:

Davisson-Germer's experiment showed that electron beams can undergo diffraction when passed through atomic crystals. This shows the wave nature of electrons as waves can exhibit interference and diffraction.

The diffraction and the interference pattern of an electron were observed during the Davisson and Germer experiment hence it establishes the wave nature of the electron.

Hence, the answer is the option (3).

Example 2: The Davisson-Germer experiment involves the diffraction of electrons by a crystal lattice. The figure below shows a typical diffraction pattern obtained in the experiment.

If the lattice spacing of the nickel crystal is 0.092 nm, what is the angle of diffraction for the first-order peak when the accelerating voltage of the electrons is 54 V?

1) $26.4^{\circ}$
2) $65^{\circ}$
3) $36.4^{\circ}$
4) $41.2^{\circ}$

Solution:

In the Davisson-Germer experiment, a beam of electrons is accelerated towards a nickel crystal. The electrons are diffracted by the crystal lattice and produce a diffraction pattern on a screen behind the crystal.

The diffraction pattern consists of a series of peaks that correspond to different angles of diffraction. The angle of diffraction is given by

$\sin \theta=\frac{n \lambda}{2 d}$

where $\theta$ is the angle of diffraction, n is the order of the diffraction peak, $\lambda$ is the de Broglie wavelength of the electrons, and d is the lattice spacing of the crystal.

The de Broglie wavelength of an electron is given by:

$\lambda=\frac{h}{p}$

where h is Planck's constant and p is the momentum of the electron. The momentum of an electron is given by:

$p=\sqrt{2 m_e E}$

where $m_e$ is the mass of an electron and E is the kinetic energy.

Substituting the given values, we get:

$\lambda=\frac{h}{\sqrt{2 m_e E}}=\frac{6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}}{\sqrt{2 \times 9.109 \times 10^{-31} \mathrm{~kg} \times 54 \mathrm{~V}}}=0.167 \mathrm{~nm}$

Substituting the values into the formula for the angle of diffraction, we get:

$\sin \theta=\frac{1 \times 0.167 \mathrm{~nm}}{2 \times 0.092 \mathrm{~nm}}=0.9087$

Taking the inverse sine of both sides, we get:

$\theta=\sin ^{-1} 0.9087=65.32$

where $\theta$ is the angle between the incident rays and the surface of the crystal And also $\theta$ is the angle of diffraction

$\begin{aligned} & \text { (Now For } \phi=\text { scattering angle } \\ & \text { As } \theta+\phi+\theta=180^{\circ} \\ & \text { So } \phi=180-2 \theta \\ & \text { so } \phi=50^{\circ} \text { ) }\end{aligned}$

Example 3: What is the function of the collimator in the Davisson-Germer experiment?

1) To detect scattered electrons

2) To produce a beam of electrons

3) To accelerate electrons

4) To rotate the nickel crystal

Solution:

The Davisson-Germer experiment and the Frank Hertz experiment. The Davisson-Germer experiment demonstrated the wave nature of electrons through electron diffraction and verified the de Broglie equation. The experimental setup included an electron gun, collimator, target, and detector. The scattered electrons produced a diffraction pattern and the dual nature of matter was verified. The Frank Hertz experiment verified the existence of discrete energy states in atoms, and the graph of collected current vs accelerating voltage showed a characteristic 4.9 V peak due to the ionization of mercury atoms. The collimator in the Davisson-Germer experiment is used to produce a narrow and straight beam of electrons ready for acceleration.

Hence, the answer is the option (2).

Example 4: What is the significance of the maximum intensity of the scattered electron beam in the Davisson-Germer experiment?

1) It is the result of the destructive interference of the scattered electrons.

2) It verifies the particle nature of electrons.

3) It is the result of the constructive interference of the scattered electrons.

4) It disproves the de Broglie equation.

Solution:

The Davisson-Germer experiment and the Frank Hertz experiment. The Davisson-Germer experiment demonstrated the wave nature of electrons through electron diffraction and verified the de Broglie equation. The experimental setup included an electron gun, collimator, target, and detector. The scattered electrons produced a diffraction pattern and the dual nature of matter was verified. The Frank Hertz experiment verified the existence of discrete energy states in atoms, and the graph of collected current vs accelerating voltage showed a characteristic 4.9 V peak due to the ionization of mercury atoms.

The maximum intensity of the scattered electron beam in the Davisson-Germer experiment is the result of the constructive interference of the scattered electrons.

Hence, the answer is the option (3).

Example 5: The X-ray diffraction pattern of a crystal is given below. It undergoes first-order reflection at a Bragg angle of 30 degrees from a crystal. What is the value of the interplanar spacing (d) of the crystal, given that the X-ray wavelength used is 0.15 nm?

1) 0.10 nm

2) 0.15 nm

3) 0.20 nm

4) 0.25 nm

Solution:

The given X-ray diffraction pattern is due to the constructive interference of X-rays diffracted by the crystal planes. According to Bragg's law, the condition for constructive interference is given by $2 d \sin \theta=n \lambda$ , where d is the interplanar spacing, $\theta$ is the angle of incidence,$\lambda$ is the wavelength of the X-rays, and n is an integer.

It undergoes first-order reflection at a Bragg angle of 30 degrees from a crystal.

Therefore, we can calculate the interplanar spacing (d) using the formula:

$\begin{aligned} & 2 d \sin \theta=n \lambda \\ & 2 d \sin 30^{\circ}=1(0.15 \mathrm{~nm}) \\ & d=\frac{0.15 \mathrm{~nm}}{2 \sin 30^{\circ}} \\ & d=\frac{0.15 \mathrm{~nm}}{1} \\ & \mathrm{~d}=0.15 \mathrm{~nm}\end{aligned}$

For more information and understanding of the topic below video can be referred:

Summary

The Davisson-Germer experiment (1927) provided direct evidence of the wave nature of electrons by demonstrating electron diffraction through a nickel crystal, thus confirming de Broglie's wave-particle duality hypothesis. This discovery has had profound implications, including the development of electron microscopes and advancements in quantum physics. Similarly, the Frank-Hertz experiment (1914) validated the existence of quantized energy levels in atoms, aligning with Bohr's model and underpinning our understanding of atomic structure. Both experiments are cornerstones in quantum mechanics, highlighting the dual nature of matter and energy.