Equation Of Path Of A Projectile

Edited By Vishal kumar | Updated on Jul 02, 2025 05:44 PM IST

Understanding the path of a projectile is crucial in physics, as it combines principles of motion and forces. The equation of a projectile's path describes how an object moves under the influence of gravity after being launched.

In this article, we will cover the concept of the equation of the path of the projectile. This concept falls under the broader category of kinematics which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept. And for NEET two questions were asked from this concept.

This Story also Contains

Equation of Path of a Projectile
Solved Question Besed On Equation Of Path Of A Projectile
Summary

Equation Of Path Of A Projectile

Projectile Motion

Two-dimensional motions under the action of the uniform force are called projectile motion.

E.g- A javelin thrown by an athlete

Projectile Projected at an angle 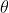$\theta$

Initial Velocity- u

Horizontal component $=u_x=u \cos \theta$
Vertical component $=u_y=u \sin \theta$
Final velocity $=\mathrm{V}$
Horizontal component $=V_x=u \cos \theta$
Vertical component $=V_y=u \sin \theta-g . t$

So,

$V=\sqrt{V_x^2+V_y^2}$

Displacement = S

Horizontal component $=S_x=u \cos \theta . t$
Vertical component $=S_y=u \sin \theta \cdot t-\frac{1}{2} \cdot g \cdot t^2$

and, $\quad S=\sqrt{S_x^2+S_y^2}$
Acceleration $=\mathrm{a}$
Horizontal component $=0$
Vertical component $=-g$
So, $a=-g$

Parameters In Projectile Motion

1) Maximum Height -

Maximum vertical distance attained by a projectile during its journey.

Formula,

$H=\frac{U^2 \sin ^2 \theta}{2 g}$

When the velocity of the projectile increases n time then the Maximum height is increased by a factor of $n^2$

Special Case: If U is doubled, H becomes four times provided $\theta \& \mathrm{~g}$ is constant.

2) Time of Flight -

Time for which projectile remains in the air above the horizontal plane.

Formula,

$T=\frac{2 u \sin \theta}{g}$

Time of ascent $= t_a=\frac{T}{2}$

Time of descent $= t_d=\frac{T}{2}$

Notes:

When the velocity of the projectile increases n time then the Time of ascent becomes n times.
When the velocity of the projectile increases n time then the Time of descent becomes n times.
When the velocity of the projectile increases n time then the time of flight becomes n times.

3) Horizontal Range

Horizontal distance travelled by a projectile from the point of the projectile to the point on the ground where it hits.

Formula,

$R=\frac{u^2 \sin 2 \theta}{g}$

The special case of horizontal range:

For max horizontal range.

$ \begin{aligned}
\theta & =45^0 \\
R_{\max } & =\frac{u^2 \sin 2(45)}{g}=\frac{u^2 \times 1}{g}=\frac{u^2}{g}
\end{aligned}$

Range remains the same whether the projectile is thrown at an $\text { angle } \theta \text { with the horizontal or at an angle } \theta \text { with vertical }(90-\theta)$ with horizontal.
When the velocity of the projectile increases n time then the horizontal range is increased by a factor of $n^2$
When the horizontal range is n times the maximum height then,

$$\tan \theta=\frac{4}{n} $$

Equation of Path of a Projectile

$
y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}
$$
or-
$$
y=x \tan \theta\left(1-\frac{x}{R}\right)
$

Where R is the horizontal range of the projectile.

It is the equation of the parabola, So the trajectory/path of the projectile is

parabolic in nature

$g \rightarrow$ Acceleration due to gravity
$u \rightarrow$ initial velocity
$\theta=$ Angle of projection

Solved Question Besed On Equation Of Path Of A Projectile

Example 1: The trajectory of a projectile near the surface of the earth is given as $y=2 x-9 x^2$. If it were launched at an angle $\theta_0$ with speed $v_0$ then $\left(g=10 \mathrm{~ms}^{-2}\right)$ :

1) $\theta_0=\sin ^{-1}\left(\frac{2}{\sqrt{5}}\right)$ and $v_0=\frac{3}{5} m s^{-1}$
2) $\theta_0=\cos ^{-1}\left(\frac{2}{\sqrt{5}}\right)$ and $v_0=\frac{3}{5} m s^{-1}$
3) $\theta_0=\cos ^{-1}\left(\frac{1}{\sqrt{5}}\right)$ and $v_0=\frac{5}{3} m s^{-1}$
4) $\theta_0=\sin ^{-1}\left(\frac{1}{\sqrt{5}}\right)$ and $v_0=\frac{5}{3} m s^{-1}$

Solution:

Given :
$
y=2 x-9 x^2
$

The standard equation of trajectory for a projectile
$
y=x \tan \theta_0-\frac{g x^2}{2 v_0^2 \cos ^2 \theta_0}
$

On comparing Eq. (1) and (2)
$
\begin{aligned}
& \tan \theta_0=2 \\
& \Rightarrow \theta_0=\sin ^{-1}\left(\frac{2}{\sqrt{5}}\right)=\cos ^{-1}\left(\frac{1}{\sqrt{5}}\right) \\
& \frac{g}{2 v_0^2 \cos ^2 \theta_0}=9 \\
& \Rightarrow \frac{g}{2 v_0^2 \times \frac{1}{5}}=9 \\
& \Rightarrow \frac{10 \times 5}{2 \times 9}=v_0^2 \\
& \Rightarrow v_0^2=\frac{25}{9} \\
& v_0=\frac{5}{3} \mathrm{~m} / \mathrm{s}
\end{aligned}
$

Hence, the answer is the Option (3).

Example 2: A particle just clears a wall of height b at a distance a and strikes the ground at a distance c from the point of projection. The angle of projection is:

1) $\tan ^{-1}\left(\frac{b c}{a(c-a)}\right)$
2) $\tan ^{-1}\left(\frac{b c}{a}\right)$
3) $\tan ^{-1}\left(\frac{b}{a * c}\right)$
4) $45^{\circ}$

Solution:

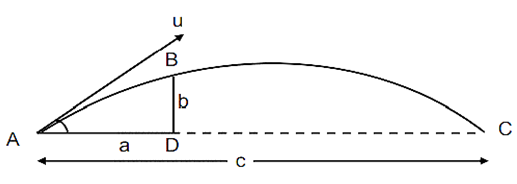
$\begin{aligned}
& a=(u \cos \alpha) t \text { and } \\
& b=(u \sin \alpha) t-\frac{1}{2} g t^2 \\
& b=a \tan \alpha-\frac{1}{2} g \frac{a^2}{u^2 \cos ^2 \alpha} \\
& \text { also, } c=\frac{u^2 \sin 2 \alpha}{g} \\
& \Rightarrow b=a \tan \alpha-\frac{a^2 g}{2}\left(\frac{\sin 2 \alpha}{c g}\right) \sec ^2 \alpha \\
& \Rightarrow b=a \tan \alpha-\frac{a^2}{2 c} 2 \tan \alpha \\
& \Rightarrow\left(a-\frac{a^2}{c}\right) \tan \alpha=b \\
& \Rightarrow \tan \alpha=\frac{b c}{a(c-a)}
\end{aligned}$

Hence, the answer is option (1).

Example 3: $ \text { Position of a particle moving in } x-y \text { plane as a function of time } t \text { is } 2 t \hat{i}+4 t^2 \hat{j} \text {. The equation of the trajectory of the particle is : }$

1) $ y=x^2 $
2) $ y=2 x $
3) $ y^2=x $
4) $ y=x $

Solution:

$
\begin{aligned}
& \mathrm{x}=2 \mathrm{t} \Rightarrow \mathrm{t}=\mathrm{x} 2 \\
& \mathrm{y}=4 \mathrm{t}^2 \\
& \text { put } \mathrm{t}=\mathrm{x} / 2 \text { we get } \mathrm{y}=4 \mathrm{xx}^2 / 4 \\
& \mathrm{y}=\mathrm{x}^2 \\
& X=2 t \\
& Y=4 t^2 \\
& Y=x^2
\end{aligned}
$

Hence, the answer is the option (1).

Example 4: A projectile is given an initial velocity of $(\hat{i}+2 \hat{j}) \mathrm{m} / \mathrm{s}$, where $\hat{i}$ is along the ground and $\hat{j}$ is along the vertical. If $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$, the equation of its trajectory is :

1) $4 y=2 x-25 x^2$
2) $y=x-5 x^2$
3) $y=2 x-5 x^2$
4) $4 y=2 x-5 x^2$

Solution:

Given :
$
\vec{u}=\hat{i}+2 \hat{j}
$

From the equation of motion,
$
\begin{aligned}
& \vec{s}=\vec{u} t+\frac{1}{2} a t^2 \\
& \Rightarrow \overrightarrow{r_f}-\overrightarrow{r_i}=(\hat{i}+2 \hat{j}) t+\frac{1}{2}(-g \hat{j}) t^2 \\
& \Rightarrow \overrightarrow{r_f}-0=t \hat{i}+2 t \hat{j}-\frac{g}{2} t^2 \hat{j} \\
& \Rightarrow x \hat{i}+y \hat{j}=t \hat{i}+\left(2 t-\frac{g}{2} t^2\right) \hat{j}
\end{aligned}
$

After comparing both sides, we get,
$
x=t \text { and } y=\left(2 t-5 t^2\right)
$

Now, put the value of $\mathrm{t}$ in $y=\left(2 t-5 t^2\right)$

$\text{Note: the above question is solved by the basic method of kinematical equation motion but you can also solve this question by the equation of trajectory of projectile motion. Hint for alternate method :}$
$
y=x \tan \theta\left(1-\frac{x}{R}\right)
$
$\mathrm{OR}$,
$
y=x \tan \theta-\frac{1}{2} \frac{x^2 g}{u^2 \cos ^2 \theta}
$

Hence, the answer is the option (3).

Example 5: A body of mass $10 \mathrm{~kg}$ is projected at an angle of $45^{\circ}$ with the horizontal. The trajectory of the body is observed to pass through a point $(20,10)$. If $\mathrm{T}$ is the time of flight, then its momentum vector, at time $\mathrm{t}=\frac{\mathrm{T}}{\sqrt{2}}$ $\qquad$
$\left[\right.$ Take $\left.g=10 \mathrm{~m} / \mathrm{s}^2\right]$
$\left[\text { Take } g=10 \mathrm{~m} / \mathrm{s}^2\right]$

1) $100 \mathrm{i}+(100 \sqrt{2}-200) \mathrm{j}$
2) $100 \sqrt{2} \hat{\mathrm{i}}+(100-200 \sqrt{2}) \hat{\mathrm{j}}$
3) $100 \hat{\mathrm{i}}+(100-200 \sqrt{2}) \hat{\mathrm{j}}$
4) $100 \sqrt{2} \hat{\mathrm{i}}+(100 \sqrt{2}-200) \hat{\mathrm{j}}$

Solution:

$
\mathrm{m}=10 \mathrm{~kg}
$

We know that the equation of trajectory is
$
\begin{aligned}
& \mathrm{y}=\mathrm{x} \tan \theta\left(1-\frac{\mathrm{x}}{\mathrm{R}}\right) \\
& 10=20\left(\tan 45^{\circ}\right)\left(1-\frac{20}{\mathrm{R}}\right) \\
& \frac{1}{2}=1-\frac{20}{\mathrm{R}} \\
& \frac{1}{2}=\frac{20}{\mathrm{R}} \\
& \mathrm{R}=40 \rightarrow(1)
\end{aligned}
$

Also, we know that,

$\begin{aligned}
& \mathrm{R}=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}} \\
& 40=\frac{\mathrm{u}^2 \sin 90^{\circ}}{10} \\
& \mathrm{u}^2=400 \\
& \mathrm{u}=20 \mathrm{~m} / \mathrm{s} \rightarrow(2) \\
& \text { At } \mathrm{t}=\frac{\mathrm{T}}{\sqrt{2}} \\
& \overline{\mathrm{V}}=\overline{\mathrm{v}}_{\mathrm{x}}+\overline{\mathrm{V}}_{\mathrm{y}} \\
& =\mathrm{u} \cos \theta(\hat{\mathrm{i}})+(\mathrm{u} \sin \theta-\mathrm{g}) \hat{\jmath} \\
& =10 \sqrt{2} \hat{\mathrm{i}}+\left(10 \sqrt{2}-10 \times \frac{\mathrm{T}}{\sqrt{2}}\right) \hat{\jmath} \\
& \text { But } \mathrm{T}=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}=\frac{2 \times 20 \times}{10} \frac{1}{\sqrt{2}}
\end{aligned}$

$\begin{aligned}
& \mathrm{T}=2 \sqrt{2} \\
& \overline{\mathrm{v}}=10 \sqrt{2} \hat{\mathrm{i}}+(10 \sqrt{2}-20) \hat{\jmath} \\
& \therefore \text { Momentum vector }=\overline{\mathrm{P}}=\mathrm{m} \overline{\mathrm{v}} \\
& \overline{\mathrm{P}}=100 \sqrt{2} \hat{\mathrm{i}}+(100 \sqrt{2}-200) \hat{\mathrm{j}}
\end{aligned}$

Hence, the answer is option (1).

Summary

In summary, the equation of the path of a projectile is one of the cornerstone equations of physics, permitting great precision in the prediction and, hence, analysis of such described trajectories of the objects thrown into the atmosphere. This general movement, forming a parabola, due to the known movements under the law of the earth's gravity force in action, is core to understanding and optimizing the trajectory of the moving projectiles in different real-life scenarios.

Frequently Asked Questions (FAQs)

1. What is the equation of the path of a projectile?

The equation of the path of a projectile is y = x tan θ - (gx^2)/(2v0^2 cos^2 θ), where y is the vertical position, x is the horizontal position, θ is the launch angle, g is the acceleration due to gravity, and v0 is the initial velocity. This equation describes a parabola in the x-y plane.

2. What is the significance of the coefficient of x in the projectile equation?

The coefficient of x in the equation, tan θ, represents the initial slope of the projectile's path. It determines the initial direction of the projectile's motion and is directly related to the launch angle.

3. Why is the path of a projectile a parabola?

The path of a projectile is a parabola because it combines two types of motion: constant velocity in the horizontal direction and uniformly accelerated motion in the vertical direction due to gravity. The combination of these motions results in a parabolic trajectory.

4. Does air resistance affect the equation of the projectile's path?

Yes, air resistance affects the equation of the projectile's path. The equation y = x tan θ - (gx^2)/(2v0^2 cos^2 θ) assumes no air resistance. In reality, air resistance causes the path to deviate from a perfect parabola, typically resulting in a shorter range and a slightly asymmetrical trajectory.

5. How does gravity influence the projectile's path equation?

Gravity (g) appears in the second term of the equation: -(gx^2)/(2v0^2 cos^2 θ). It causes the downward curvature of the parabola. A stronger gravitational field (larger g) results in a more pronounced curvature and shorter range.

6. What assumptions are made in deriving the standard projectile path equation?

The standard projectile path equation assumes: 1) no air resistance, 2) constant gravitational acceleration, 3) flat, horizontal ground, 4) the projectile is treated as a point mass, and 5) the Earth's curvature and rotation are negligible for the distances involved.

7. Can the projectile equation be used to determine the time of flight?

While the projectile equation doesn't directly give the time of flight, it can be used in conjunction with the equations of motion to find it. By setting y = 0 and solving for x to find the range, you can then use the horizontal motion equation x = v0 cos θ * t to solve for the total time of flight.

8. How does the coefficient of restitution affect the projectile's path after bouncing?

The coefficient of restitution affects the projectile's path after bouncing by determining how much kinetic energy is conserved in the collision. A higher coefficient results in a bouncier collision, leading to a new projectile path with a higher initial velocity. The new path would be described by a new equation with updated initial conditions.

9. How can the projectile equation be used to analyze the motion of a projectile in a resistant medium?

The standard projectile equation assumes no air resistance. To analyze motion in a resistant medium, the equation needs to be modified to include drag forces. This typically results in a more complex differential equation that may not have a simple analytical solution. Numerical methods are often used to approximate the trajectory in these cases.

10. How does the curvature of the Earth affect the projectile equation for long-range projectiles?

For very long-range projectiles, the curvature of the Earth becomes significant. The standard projectile equation assumes a flat Earth and doesn't account for this curvature. For such cases, a modified equation using spherical coordinates or a numerical approach considering the changing direction of gravity is necessary.

11. How does changing the launch angle affect the shape of the projectile's path?

Changing the launch angle affects the shape of the projectile's path by altering the ratio of initial vertical velocity to horizontal velocity. A higher launch angle results in a steeper, narrower parabola, while a lower angle produces a flatter, wider parabola. The optimal angle for maximum range is 45 degrees in the absence of air resistance.

12. How does initial velocity affect the projectile's path equation?

Initial velocity (v0) appears in the denominator of the second term in the equation: y = x tan θ - (gx^2)/(2v0^2 cos^2 θ). A higher initial velocity results in a flatter trajectory and longer range, while a lower initial velocity leads to a more curved path and shorter range.

13. Can the projectile equation be used to find the maximum height of the projectile?

Yes, the projectile equation can be used to find the maximum height. At the highest point, the vertical velocity is zero. By setting the derivative of y with respect to x equal to zero and solving for x, you can find the x-coordinate of the highest point. Substituting this x-value back into the original equation gives the maximum height.

14. How is the range of a projectile related to its path equation?

The range of a projectile is the horizontal distance it travels before returning to its initial height. It can be found by setting y = 0 in the path equation and solving for x. The resulting expression for range is R = (v0^2 sin 2θ)/g, which is derived from the path equation.

15. How does the projectile's path equation change on different planets?

The projectile's path equation remains the same on different planets, but the value of g (gravitational acceleration) changes. For example, on Mars where g is about 3.7 m/s^2, the parabola would be less curved and the projectile would have a longer range compared to Earth (g ≈ 9.8 m/s^2) for the same initial conditions.

16. Can the projectile equation be used to determine the velocity at any point along the path?

While the projectile equation itself doesn't directly give velocity, it can be used to find velocity components at any point. By differentiating y with respect to time (using the chain rule and dx/dt = v0 cos θ), you can obtain the vertical velocity component. The horizontal velocity component remains constant at v0 cos θ.

17. What is the relationship between the projectile's path equation and its energy?

The projectile's path equation is related to its energy through the principle of conservation of energy. At any point on the path, the sum of kinetic and potential energy remains constant. The height y in the equation directly relates to gravitational potential energy, while the slope of the path at any point relates to the ratio of vertical to horizontal kinetic energy.

18. How does the projectile equation change in a rotating reference frame, such as on a rotating planet?

In a rotating reference frame, like on the surface of a rotating planet, the projectile equation needs to account for the Coriolis effect and centrifugal force. These additional terms cause the projectile's path to deviate from a simple parabola. The modified equation becomes more complex and often requires numerical solutions.

19. How can the projectile equation be used to analyze the motion of a projectile in a non-inertial reference frame?

In a non-inertial reference frame (like a rotating or accelerating frame), the standard projectile equation doesn't apply directly. Additional terms need to be added to account for fictitious forces like the Coriolis force and centrifugal force. The resulting equation becomes more complex and often requires numerical methods to solve, as the path may not be a simple parabola in the non-inertial frame.

20. What is the physical meaning of the term (gx^2)/(2v0^2 cos^2 θ) in the projectile equation?

The term (gx^2)/(2v0^2 cos^2 θ) represents the vertical displacement due to gravity. It shows how much the projectile has fallen below the straight-line path it would follow if there were no gravity. This term increases quadratically with x, causing the downward curvature of the parabola.

21. How can you use the projectile equation to find the angle of impact?

To find the angle of impact, take the derivative of y with respect to x in the projectile equation: dy/dx = tan θ - (gx)/(v0^2 cos^2 θ). Evaluate this at the point of impact (where the projectile hits the ground) to get the slope of the path at that point. The arctangent of this slope gives the angle of impact.

22. What is the relationship between the projectile's path equation and its velocity components?

The projectile's path equation is derived from its velocity components. The horizontal velocity component (v0 cos θ) remains constant and determines the x-coordinate: x = (v0 cos θ)t. The vertical velocity component (v0 sin θ - gt) is integrated to get the y-coordinate, which leads to the path equation.

23. How does the projectile equation change for a projectile launched from a height?

For a projectile launched from a height h, the equation becomes y = h + x tan θ - (gx^2)/(2v0^2 cos^2 θ). The only change is the addition of the initial height h to the right side of the equation. This shifts the entire parabola upward by h units.

24. How does the projectile equation relate to the concept of symmetry in projectile motion?

The projectile equation reveals the symmetry of projectile motion. The parabola is symmetrical about its vertex, which occurs at the highest point of the trajectory. This symmetry is reflected in the equation: the linear term (x tan θ) represents the upward part of the motion, while the quadratic term (-(gx^2)/(2v0^2 cos^2 θ)) causes the downward curvature, creating a balanced parabolic shape.

25. What is the significance of the discriminant in the projectile equation when solving for range?

When solving the projectile equation for range (setting y = 0), the discriminant of the resulting quadratic equation determines the nature of the solutions. A positive discriminant indicates two solutions (the projectile hits the ground twice), zero discriminant means one solution (the projectile just grazes the ground), and a negative discriminant means no real solutions (the projectile doesn't reach the ground).

26. Can the projectile equation be used to determine the optimal launch angle for maximum range?

Yes, the projectile equation can be used to determine the optimal launch angle for maximum range. By expressing the range R in terms of the launch angle θ (R = (v0^2 sin 2θ)/g) and finding the maximum of this function, you can show that the optimal angle is 45° in the absence of air resistance.

27. How does the projectile equation change in a non-uniform gravitational field?

In a non-uniform gravitational field, the standard projectile equation doesn't apply. The acceleration due to gravity g would be a function of position rather than a constant. This results in a more complex differential equation that typically requires numerical methods to solve, as the path may not be a simple parabola.

28. What is the significance of the vertex form of the projectile equation?

The vertex form of the projectile equation, y = -a(x-h)^2 + k, where (h,k) is the vertex of the parabola, is particularly useful for finding the maximum height and the x-coordinate at which it occurs. It also clearly shows the symmetry of the path about the vertical line x = h.

29. How can the projectile equation be used to analyze the motion of a projectile launched at an angle downhill or uphill?

For a projectile launched at an angle downhill or uphill, the standard equation needs to be modified. The ground is no longer horizontal, so a coordinate rotation is applied. The new equation will have additional terms that account for the angle of the slope. This affects both the range and the optimal launch angle.

30. What is the relationship between the projectile equation and the equations of uniform circular motion?

While the projectile equation describes parabolic motion and uniform circular motion involves circular paths, both are examples of two-dimensional motion. In fact, a projectile's path can be seen as part of an extremely elongated ellipse, of which a circle is a special case. The connection becomes more apparent when considering orbital motion, where the projectile equation evolves into equations of elliptical orbits.

31. How does the projectile equation relate to the concept of independence of horizontal and vertical motions?

The projectile equation y = x tan θ - (gx^2)/(2v0^2 cos^2 θ) embodies the principle of independence of horizontal and vertical motions. The x-term (x tan θ) represents the straight-line path the projectile would follow without gravity, while the x^2 term shows the effect of gravity. This separation reflects how horizontal motion (constant velocity) and vertical motion (uniformly accelerated) are independent but combine to create the parabolic path.

32. Can the projectile equation be used to analyze the motion of a projectile with varying mass?

The standard projectile equation assumes constant mass. For a projectile with varying mass (like a rocket burning fuel), the equation needs to be modified. The changing mass affects the acceleration, leading to a more complex differential equation. In such cases, the path may deviate significantly from a parabola, and numerical methods are often required for analysis.

33. What is the relationship between the projectile equation and the concept of parametric equations in mathematics?

The projectile motion can be described using parametric equations, where x and y are expressed as functions of time t: x = (v0 cos θ)t and y = (v0 sin θ)t - (1/2)gt^2. The standard projectile equation is derived by eliminating the parameter t from these equations. This parametric form is often more useful for solving certain types of problems and illustrates the connection between projectile motion and parametric representations in mathematics.

34. How can the projectile equation be used to analyze the motion of a projectile in a medium with altitude-dependent air resistance?

For a projectile moving through a medium with altitude-dependent air resistance, the standard equation doesn't apply. The drag force would be a function of both velocity and altitude, leading to a system of coupled differential equations. These equations typically don't have simple analytical solutions and require numerical methods for accurate analysis.

35. What is the significance of the initial velocity vector in the projectile equation?

The initial velocity vector, represented by v0 and θ in the equation, is crucial as it determines the initial conditions of the projectile's motion. It sets both the speed and direction at launch, influencing the range, maximum height, and overall shape of the trajectory. The components of this vector (v0 cos θ and v0 sin θ) appear in the equation and directly affect the coefficients of x and x^2 terms.

36. How does the projectile equation relate to the concept of vector addition in physics?

The projectile equation is a result of vector addition of two motions: constant velocity motion in the horizontal direction and uniformly accelerated motion in the vertical direction. At any given time, the projectile's position vector is the sum of these two component vectors. The equation y = x tan θ - (gx^2)/(2v0^2 cos^2 θ) is essentially a scalar representation of this vector addition process.

37. Can the projectile equation be used to analyze the motion of a projectile affected by wind?

The standard projectile equation doesn't account for wind. To analyze a projectile affected by wind, you need to modify the equation to include wind velocity components. This typically results in additional terms in both x and y directions. For constant wind, the path remains parabolic but is shifted. For varying wind, the path may deviate significantly from a parabola and often requires numerical analysis.

38. How does the projectile equation change for a projectile launched from a moving platform?

For a projectile launched from a moving platform, the initial velocity in the equation needs to be modified to include the velocity of the platform. If the platform's motion is uniform, this effectively changes the initial velocity vector (both magnitude and direction). The resulting equation will still describe a parabola, but with different parameters. If the platform's motion is accelerated, the problem becomes more complex and may require a different approach.

39. What is the relationship between the projectile equation and the equations of orbital motion?

The projectile equation describes motion under constant gravitational acceleration near Earth's surface, while orbital motion equations describe movement under varying gravitational force at larger distances. As the initial velocity of a projectile increases, its path transitions from a parabola to an ellipse, then to a parabola again (escape velocity), and finally to a hyperbola. The projectile equation can be seen as a special case of the more general orbital equations for motion close to Earth's surface.

40. What is the significance of the quadratic nature of the projectile equation?

The quadratic nature of the projectile equation (y being a quadratic function of x) is significant because it results in a parabolic path. This quadratic relationship arises from the linear time dependence of horizontal position and the quadratic time dependence of vertical position due to constant acceleration. The quadratic term represents the effect of gravity, causing the down