Isobaric Process

An isobaric process is a thermodynamic scenario where the pressure remains constant while the volume and temperature of a system might change. This concept is particularly relevant when studying the behaviour of gases in various conditions, such as in weather systems or car engines. For students preparing for board exams and competitive exams like JEE and NEET, understanding an isobaric process is crucial for solving problems related to gas laws and heat transfer. This article explains the isobaric process in simple terms and includes a solved example to illustrate how these principles are applied in real-life situations.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Definition of Isobaric Process
2. Solved Examples Based on the Isobaric Process
3. Summary

Definition of Isobaric Process

Isobaric Process- A Thermodynamic process in which pressure remains constant is known as the isobaric process.

In this process, V and T change keeping P constant. I.e Charle’s law is obeyed in this process

Key points in the Isobaric Process

- Its Equation of state is given as $\frac{V}{T}=$ constant
I.e $\frac{V_1}{T_1}=\frac{V_2}{T_2}=$ constant
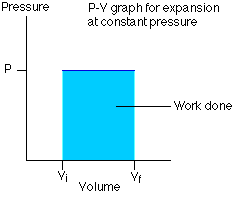
- P-V Indicator diagram for an isobaric process
Its PV graph has slope $=0$ (i.e $\frac{d P}{d V}=0$ )

The above Graph represents an isobaric expansion.

The P-V diagram for this process is a line is parallel to the volume line.

• Specific heat of gas during the isobaric process is given by

$C_P=\left(\frac{f}{2}+1\right) R$

• The bulk modulus of elasticity during the isobaric process is given by

$K=\frac{\Delta P}{-\Delta V / V}=0$

• Work done in the isobaric process-

$
\Delta W=\int_{V_i}^{V_f} P d V=P \int_{V_i}^{V_f} d V=P\left[V_f-V_i\right]
$

Or we can write
$
\Delta W=P\left(V_f-V_i\right)=n R\left[T_f-T_i\right]=n R \Delta T
$

• Internal energy in an isobaric process

$\Delta U=n C_V \Delta T=n \frac{R}{(\gamma-1)} \Delta T$

• Heat in an isobaric process

From FLTD $\Delta Q=\Delta U+\Delta W$
$
\begin{aligned}
& \quad \Delta Q=n \frac{R}{(\gamma-1)} \Delta T+n R \Delta T=n R \Delta T\left[\frac{1}{\gamma-1}+1\right] \\
& \text { So } \Rightarrow \Delta Q=n R \Delta T \frac{\gamma}{\gamma-1}=n\left(\frac{\gamma}{\gamma-1}\right) R \Delta T=n C_p \Delta T \\
& \\
& \quad \text { So } \Delta Q=n C_p \Delta T
\end{aligned}
$

• Examples of the isobaric process

1. Conversion of water into vapour phase (boiling process)

From the first law of thermodynamics

$\Delta Q=\Delta U+\Delta W=\Delta U_K+\Delta U_P+\Delta W$

since $\Delta U_K=0$ [as there is no change in temperature] and using,
$
\Delta Q=m L
$
$
\begin{aligned}
\Delta Q & =\Delta U_P+P\left[V_f-V_i\right] \\
\Delta U_P & =\Delta Q-P\left[V_f-V_i\right] \\
\Delta U_P & =m L-P\left[V_f-V_i\right]
\end{aligned}
$

Here, i- initial state and f- final state

2. Conversion of ice into water

From FLOT $\quad \Delta Q=\Delta U+\Delta W$
and using, $\Delta Q=m L$
we get $m L=\Delta U_P+\Delta U_K+\Delta W$
$
m L=\Delta U_P+\Delta U_K+P\left(V_f-V_i\right)
$
since $\Delta U_K=0$ [as there is no change in temperature]
and $\Delta W=0 \quad$ [As $V_f-V_i$ is negligible, I.e, when ice converts into water then changes in volume, is negligible]

Hence $\Delta U_P=m L$

Recommended Topic Video

Solved Examples Based on the Isobaric Process

Example 1: When heat is given to a system in an isobaric process, then

1) The work is done by the gas

2) The internal energy of the gas increases

3) Both a and b

4) None from a and b

Solution:

Isobaric process

A Thermodynamic process in which pressure remains constant.

wherein

$\begin{aligned} & P V=n R T \\ & \because P=\text { constant } \\ & V \alpha T \\ & \frac{V_1}{T_1}=\frac{V_2}{T_2}\end{aligned}$

When heat is supplied at constant pressure, a part of it goes in the expansion of gas and the remaining part is used to increase the temperature of the gas which in turn increases the internal energy

Hence, the answer is the option 3.

Example 2: If $C_P$ and $C_V$ denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then
1) $C_P-C_V=28 / R$
2) $C_P-C_V=R / 28$
3) $C_P-C_V=R / 14$
4) $C_P-C_V=R$Solution:

Specific heat in the isobaric process

$
C_p=\left(\frac{f}{2}+1\right) R
$
- wherein
$f_{\text {is the degree of freedom }}$
Difference between molar specific heat $=\mathrm{R}$
$C_p-C_v=R \quad$ this is in per molar, we have to convert it into per mass
1 mole $=28 \mathrm{~g}$ of nitrogen.
$
\therefore C_p-C_v=\frac{R}{28}
$
where $C_{p \&} C_v$ denote specific heats of nitrogen per unit mass.

Hence, the answer is the option (2).

Example 3: A gaseous mixture consists of 16 g of helium and 16 g of oxygen. The ratio $C_P / C_V$ of the mixture is

1) 1.62

2) 1.54

3) 1.59

4) 1.4

Solution:

Specific heat in the isobaric process

$
\begin{aligned}
& C_p=\left(\frac{f}{2}+1\right) R \\
& \gamma_{\text {mix }}=\frac{n_1 C_{p 1}+n_2 C_{p 2}}{n_1 C_{v 1}+n_2 C_{v 2}}
\end{aligned}
$
wherein
$f$ is the degree of freedom
$
\begin{aligned}
& \gamma_{\text {mix }}=\frac{n_1 C_{p 1}+n_2 C_{p 2}}{n_1 C_{v 1}+n_2 C_{v 2}} \\
& n_1=\frac{16}{4}=4, C_{v 1}=\frac{3 R}{2}, C_{p 1}=\frac{5 R}{2} \\
& n_2=\frac{16}{32}=\frac{1}{2}, C_{v 2}=\frac{5 R}{2}, C_{p 2}=\frac{7 R}{2} \\
& \gamma_{\text {mix }}=\frac{10 R+\frac{7 R}{4}}{6 R+\frac{5 R}{4}} \\
& =\frac{47}{29}=1.62
\end{aligned}
$

Hence, the answer is (1.62).

Example 4: The equation of state for a gas is given by $P V=n R T+\alpha V$, where $\boldsymbol{n}$ is the number of moles and $\alpha$ is a positive constant. The initial temperature and pressure of one mole of the gas contained in a cylinder are $T_0$ and $P_0$ respectively. The work done by the gas when its temperature doubles isobarically will be :

1) $\frac{P_0 T_0 R}{P_0-\alpha}$
2) $\frac{P_0 T_0 R}{P_0+\alpha}$
3) $P_0 T_0 R \ln 2$
4) $P_0 T_0 R$

Solution:

As the Equation of state is $\mathrm{PV}=\mathrm{nRT}+\alpha \mathrm{V}$
$
\Rightarrow(P-\alpha) V=n R T \text { or } P-\alpha=\frac{n R T}{V}
$

Initial volume =
$
V_0=\frac{n R T_0}{P_0-\alpha}
$

Final volume
$
V_f=\frac{2 n R T_0}{P_0-\alpha}
$
$
\begin{aligned}
& \quad W=P \Delta V \\
& =P_0\left(V_f-V_i\right)=P_0\left[\frac{2 n R T_0}{P_0-\alpha}-\frac{n R T_0}{P_0-\alpha}\right]
\end{aligned}
$

For $\mathrm{n}=1$
$
\begin{aligned}
W & =P_0 \frac{R T_0}{P_0-\alpha} \\
W & =\frac{P_0 T_0 R}{P_0-\alpha}
\end{aligned}
$

Hence, the answer is the option (1).

Example 5: When a system undergoes a physical change in such a way that its pressure remains constant, then the bulk modulus of elasticity for the process is

1) infinite

2) one

3) zero

4) can have any value

Solution:

Bulk Modulus of elasticity in the isobaric process -

$
\begin{aligned}
& W=\int P d V^W=P\left(V_f-V_i\right) \\
& W=P\left(V_f-V_i\right)=n R\left(T_f-T_i\right)
\end{aligned}
$

The bulk modulus of elasticity
$
K=\frac{\Delta P}{-\frac{\Delta V}{V}}
$
as $\Delta P=0$ for isobaric process
So,
$
K=\frac{0}{-\frac{\Delta V}{V}}=0
$

Hence, the answer is the option 3.

Summary

In an Isobaric process, while the system volume and temperature can change, such change in temperature is directly related to work done by the ones on it. For an ideal gas, the volume-temperature relationship can be well represented by Charles’s law which says volume is proportional to temperature, provided it remains constant at any given point throughout the entire isobaric process.