Magnetic Moment Of Revolving Electron And Bohr Magneton

The magnetic moment of a revolving electron and the concept of the Bohr magneton are fundamental to understanding the magnetic properties of atoms and molecules. In essence, as an electron orbits the nucleus, it generates a magnetic field, much like a tiny loop of electric current creates a magnetic dipole. This magnetic moment is quantized, meaning it can only take on certain discrete values, a principle crucial to quantum mechanics. The Bohr magneton serves as the physical constant representing the natural unit of the electron's magnetic moment. This concept is not just theoretical; it has practical implications in various fields. For instance, the magnetic properties of materials, such as the ferromagnetism in refrigerator magnets and the functioning of MRI machines in hospitals, are deeply rooted in these quantum mechanical principles. In this article, we will understand the magnetic moment and Bohr magneton bridges the gap between microscopic quantum behaviours and macroscopic magnetic phenomena we encounter in everyday life.

This Story also Contains

1. Magnetic Dipole Moment of a Revolving Electron
2. Solved Examples Based on Magnetic Moment of Revolving Electron And Bohr Magneton
3. Summary

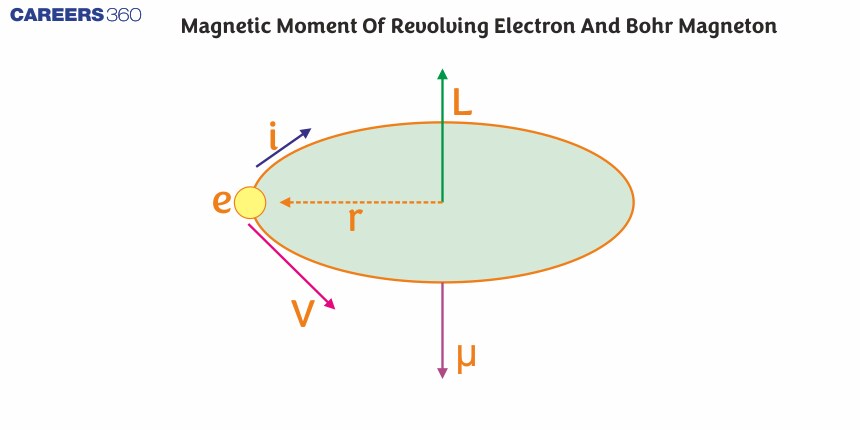
Magnetic Dipole Moment of a Revolving Electron

The magnetic dipole moment of a revolving electron is a crucial concept in quantum mechanics and electromagnetism. When an electron revolves around the nucleus of an atom, it can be thought of as a tiny loop of electric current, creating a magnetic field and behaving like a magnetic dipole.

Let us consider an electron that is revolving around in a circle of radius r with a velocity v. The charge of the electron is e and its mass is m, both of which are constant. The time period T of the electrons’ orbit is

$T=\frac{\text { Circumference }}{\text { Velocity }}=\frac{2 \pi r}{v}$

So the current due to the motion of the electron is

$i=\frac{q}{T}=\frac{-e}{\frac{2 \pi r}{v}}=\frac{-e v}{2 \pi r}$

Now, as we know the direction of current is opposite to the direction of motion of electron. Now the magnetic moment is defined as

$
\mu=i A
$

So the Magnetic moment of an electron:
$
\begin{aligned}
& \mu=\frac{-e v}{2 \pi r} A=\frac{-e v}{2 \pi r} \pi r^2 \\
& \mu=\frac{-e r v}{2}
\end{aligned}
$

If we divide and multiply by the mass of the electron,

$\mu=\frac{-e}{2 m_e} m_e v r$

As we have studied the angular momentum L is given by

$\mathrm{L}=\mathrm{mvr}$

So the above equation can be written as

$\mu=\frac{-e}{2 m_e} L$

The negative sign shows that the velocity and current are in opposite directions as shown in the figure given above. Also in the vector form, it is written as -

$\vec{\mu}=\frac{-e}{2 m_e} \vec{L}$........(I)

Now, by Niels Bohr (we have studied this particular concept in Atomic structure of Chemistry and we will study this in detail in the chapter Atoms and Nuclei of Physics), the Angular momentum of the electron is given as

$L=n \frac{h}{2 \pi}, n=0, \pm 1, \pm 2 \ldots$

Where n is the orbit quantum number and h is the Planck’s constant,

Now by using the equation (1)

$\begin{aligned} & \mu=n \frac{-e}{2 m_e} \frac{h}{2 \pi} \\ & \mu=-n \frac{e h}{4 \pi m_c}\end{aligned}$

If we put n =1, then the equation becomes

$\mu_B=-\frac{e h}{4 \pi m_e}=9.27 \times 10^{-24} \mathrm{~J} / T$

(This is called Bohr Magneton μ_B)

Recommended Topic Video

Solved Examples Based on Magnetic Moment of Revolving Electron And Bohr Magneton

Example 1: What is the approximate numerical value of Bohr Magneton?

1) $9.27 \times 10^{-25} \mathrm{~J} / \mathrm{T}$
2) $9.27 \times 10^{-27} \mathrm{~W} / \mathrm{T}$
3) $9.27 \times 10^{-24} \mathrm{~J} / \mathrm{T}$
4) $9.27 \times 10^{-25} \mathrm{~W} / \mathrm{T}$

Solution:

The magnetic moment of the electron

$\begin{aligned} \mu & =n \frac{-e}{2 m_e} \frac{h}{2 \pi} \\ \mu & =-n \frac{e h}{4 \pi m_e}\end{aligned}$

If we put n =1, then the equation becomes

$\mu_B=-\frac{e h}{4 \pi m_e}=9.27 \times 10^{-24} \mathrm{~J} / T$

(This is called Bohr Magneton. i.e μ_B)

Hence, the answer is the option (3).

Example 2: What will be the angular momentum of the revolving electron in 3^rd orbit?

1) $9.27 \times 10^{-27} \mathrm{~J} / \mathrm{T}$
2) $27.81 \times 10^{-27} \mathrm{~J} / \mathrm{T}$
3) $18.54 \times 10^{-27} \mathrm{~J} / \mathrm{T}$
4) $37.08 \times 10^{-27} \mathrm{~J} / \mathrm{T}$

Solution:

According to the magnetic moment of the revolving electron equation

$
\begin{aligned}
\mu & =n \frac{-e}{2 m_e} \frac{h}{2 \pi} \\
\mu & =-n \frac{e h}{4 \pi m_e}
\end{aligned}
$

By putting the value, $n=3$
$\mathrm{e}, \mathrm{h}$ and $\mathrm{m}_{\mathrm{e}}$ of the electron

We will get $\mu=27.81 \times 10^{-27} \mathrm{~J} / T$

Hence, the answer is the option (2).

Example 3: The momentum of an electron revolving in $\mathrm{n}^{\text {th }}$ orbit is given by : (Symbols have their usual meanings)

1) $\frac{n h}{2 \pi r}$
2) $\frac{n h}{2 \mathrm{r}}$
3) $\frac{\mathrm{nh}}{2 \pi}$
4) $\frac{2 \pi r}{n h}$

Solution:

The angular momentum of an electron in $\mathrm{n}^{\text {th }}$ orbit is.
$
\begin{aligned}
& \mathrm{L}_{\mathrm{n}}=\mathrm{mv}_{\mathrm{n}} \mathrm{r}_{\mathrm{n}}=\frac{\mathrm{nh}}{2 \pi} \\
& \mathrm{P}_{\mathrm{n}}=\mathrm{mv}_{\mathrm{n}}=\frac{\mathrm{nh}}{2 \pi \mathrm{r}_{\mathrm{n}}} \\
& \mathrm{p}_{\mathrm{n}}=\frac{\mathrm{nh}}{2 \pi \mathrm{r}}
\end{aligned}
$
Hence, the answer is the option (1).

Example 4: The magnetic moment of an electron (e) revolving in an orbit around the nucleus with an orbital angular momentum is given by :

1) $\vec{\mu}_L=\frac{\overrightarrow{\mathrm{eL}}}{2 \mathrm{~m}}$
2) $\vec{\mu}_L=-\frac{\overrightarrow{e \mathrm{~L}}}{2 \mathrm{~m}}$
3) $\overrightarrow{\mu_l}=-\frac{\overrightarrow{\mathrm{eL}}}{\mathrm{m}}$
4) $\vec{\mu}_l=\frac{2 \overrightarrow{\mathrm{eL}}}{\mathrm{m}}$

Solution:

We know that

$
\begin{aligned}
\vec{\mu}_L & =(\text { Gyromagnetic ratio }) \vec{L} \\
\vec{\mu}_L & =\left(\frac{q}{2 m}\right) \vec{L}
\end{aligned}
$

For electron,
$
\begin{aligned}
& \mathrm{q}=-\mathrm{e} \\
& \therefore \vec{\mu}_L=\left(\frac{-e}{2 m}\right) \vec{L}
\end{aligned}
$

Hence, the answer is the option (2).

Example 5: A uniform conducting wire of length is $24 a$ and resistance $R$ is wound up as a current-carrying coil in the shape of an equilateral triangle of side ' a' and then in the form of a square of side $' a^{\prime}$. The coil is connected to a voltage source $V_0$ The ratio of the magnetic moment of the coils in the case of an equilateral triangle to that of the square is $1: \sqrt{y}$ where y is__________.

1) 3

2) 4

3) 5

4) 6

Solution:

$\begin{aligned} & \text { Magnetic moment = NIA } \\ & \begin{aligned} & \text { For equilateral triangle }=A_1= \frac{1}{2} \times b \times h \\ &=\frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a \\ &=\frac{\sqrt{3} a^2}{4} \\ & h=\frac{\sqrt{3}}{2} a\end{aligned}\end{aligned}$

$\begin{aligned} & A_2=A_{\text {square }}=a^2 \\ & 24 a=N_1(3 a)=N_2(4 a) \\ & N_1=8 \\ & N_2=6\end{aligned}$
$\begin{aligned} & \frac{M_{\text {eq.triangle }}}{M_{\text {square }}}=\frac{N_1 I A_1}{N_2 I A_2} \\ &=\frac{8}{6} \times \frac{\sqrt{3} a^2}{4 \times a^2} \\ &=\frac{1}{\sqrt{3}} \\ & \therefore y=3\end{aligned}$

Summary

The magnetic moment of a revolving electron and the Bohr magneton are crucial in understanding atomic and molecular magnetism. The magnetic dipole moment arises from the electron's motion around the nucleus, quantized and represented by the Bohr magneton. This principle has practical applications, such as in ferromagnetic materials and MRI technology. Understanding these concepts bridges the gap between quantum behaviours and everyday magnetic phenomena, providing a foundation for various technological advancements.