Mechanical Properties of Solids

Introduction:
If all of the atoms in a substance are closely packed together, it is considered to be in the solid-state. The shape and dimensions of solid material are fixed. An external force must be applied to modify the shape and size of the solid item. The Mechanical Properties of Solids will be covered in this chapter.

Solids' mechanical properties define properties such as strength and deformation resistance. It represents an object's ability to endure the stress that is applied to it. Elasticity, plasticity, strength, abrasion, hardness, ductility, brittleness, malleability, and toughness are examples of mechanical qualities.

There are some notable properties and the laws governing this chapter 9 of the NCERT textbook for class 11 Physics, Mechanical Properties of Solids. At the end of the chapter, questions are posed to summarise the chapter's overall concepts and topics.

List of topics according to NCERT and JEE Main/NEET syllabus:

• Introduction to Elasticity and Plasticity
• Applications of Elastic Behaviour of Materials
• Stress and Strain
• Elastic Moduli
• Hooke’s Law and Stress-strain Curve.
• Elastic behaviour of solids
• mechanical properties of solids solutions.

Related Topics,

Important concepts discussed in mechanical properties of solids class 11 notes, Solids' mechanical properties determine their numerous qualities, such as their resistance to deformation and their strength. Resistance to deformation refers to an object's ability to resist a change in shape, whereas strength refers to an object's ability to withstand applied force. In NCERT Class 11 Physics, Chapter 9 'Mechanical Properties of Solids' is part of Unit 7 'Properties of Bulk Matter.' It is one of the most essential chapters, In the CBSE Class 11 Physics Examination, Unit 7 has a combined weightage of 20 marks alongside units 8 and 9 which is there in the syllabus. Or one, who want to learn and prepare from physics class 11 mechanical properties of solids notes pdf can refer to all different lectures and free content available.

Resistance of Deformation:

Solids are defined by their size and shape. To modify the size and shape of a solid item, an external force is necessary. If the resistance to deformation is low, an object's shape can be easily modified. The qualities of solids that define their solidity are known as mechanical properties. Plasticity, elasticity, strength, and ductility are some of these characteristics.

Elasticity is described as the property of an object that allows it to restore its original shape and size once a force has been removed. For instance, if we stretch a rubber band to a certain length and then leave it, it will revert to its previous shape.

A Perfectly Elastic Body is described as a body that returns to its original shape and size completely and instantly after the deforming force has been eliminated. Phosphor bronze and quartz fibre, for example.

Plasticity is the property of an object that causes it to change shape when a deforming force is applied and never returns to its previous shape once the deforming force is removed.

Ductility is a quality of an object that allows it to be pulled through thin wires, plates, or sheets. Consider the following scenario: Strength of Gold and Silver:

Strength is defined as the ability to withstand imposed stress without failing.

class 11 physics ch 9 ncert solutions and class 11th physics chapter 9 notes also include,

Stress:

If a body is distorted as a result of an external force, an internal force is produced at each and every section of the body that attempts to restore the body to its original state. Stress is the name for this internal energy.

Stress = F/A its unit is N/m² or Pascal.

Types of stress:

There are three types of stress:

(a) Longitudinal Stress: Longitudinal Stress occurs when the deforming force of a cylindrical body is applied normally to the area of cross-section. A change in the length of an object occurs when it is subjected to longitudinal stress.

There are two forms of longitudinal stress.-

Tensile force: Tensile stress is defined as an increase in the length of an object as a result of the applied force effect.

Compressional stress occurs when the length of an object decreases as a result of the applied force effect.

(b) Shearing or Tangential Stress: Tangential stress is defined as the restoring force per unit area when the applied force is parallel to the body's cross-sectional area. When applied tangentially, the deforming force causes changes in the shape of the body.

(c) Hydraulic Stress: Hydraulic stress refers to the restoring force that a fluid like water exerts per unit area on a body or item.

Strain:

Strain is defined as a change in the size and shape of a body caused by the application of a deforming force. Strain is defined as the proportion of a change in shape or size to the initial shape or size. It is nothing more than a number with no dimensions.

There are three different sorts of strains:

Shearing strain is the measurement of the relative displacement on opposite faces of the body caused by shearing stress.

(b) Longitudinal strain: The original length of the body changes as a result of the imposed longitudinal stress. Longitudinal strain is defined as the difference between the current length and the original length

(c) Strain of volume: Hydraulic pressure causes a strain called volume strain. The ratio of change in volume to the initial volume is what it's called. Hooke's Law states that within the elastic limit, strain and stress are proportional to each other.

Thus,

Stress ∝ Strain

Stress = k * strain

The proportionality constant K, often known as the modulus of elasticity, is used here. Hooke's law is an empirical law that holds true for most materials. Some materials, such as human muscle and rubber, defy Hooke's law.

The curve of Stress and Strain:

A line created by stress and strain is known as the stress-strain curve. A stress-strain curve for a material gives the relationship between stress and strain in the ideal case of Hooke's law. It's calculated by progressively adding load to a test coupon and measuring deformation, from which stress and strain may be calculated (see tensile testing). Many properties of a material are revealed by these curves, including Young's modulus, yield strength, and ultimate tensile strength.

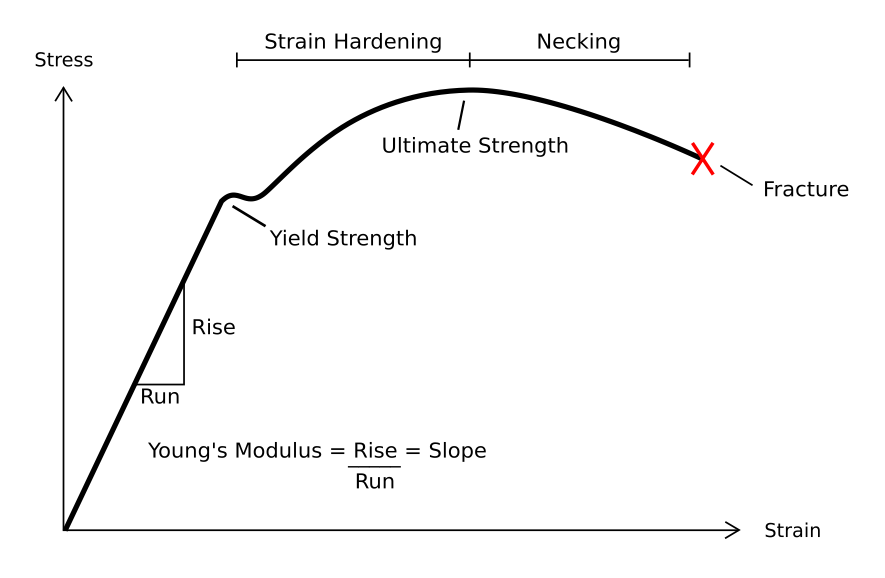
Strain

Strain is the amount of deformation experienced by the body in the direction of force applied, divided by the initial dimensions of the body.

Ε = δ/ L

is the change in length and L is the original length of the material.

The strain is a dimensionless quantity as it just defines the relative change in shape.

Elastic Moduli:

The ratio of strain and stress is known as the modulus of elasticity, or Elastic Moduli. It is one of the material's most fundamental features. Young's modulus, Shear modulus, and Bulk modulus are the three forms of elastic moduli.

Young's Rigidity Modulus:

Within the elastic limit, Young's Modulus of Rigidity is defined as the ratio of longitudinal stress to longitudinal strain. Young's Modulus is represented by the letter Y. Metals have high Young Modulus values when compared to other materials.

Y= Normal Stress / Longitudinal Strain

Bulk Modulus of Rigidity:

The ratio of normal stress to volumetric strain within the elastic limit is known as the Bulk Modulus of Rigidity. It is represented by B.

B= Normal Stress / Volumetric Strain

NCERT Notes Subject Wise Link:

• NCERT notes Class 11 Maths
• NCERT notes Class 11 Physics
• NCERT notes Class 11 Chemistry
• NCERT notes Class 11 Biology

Importance of Mechanical Properties of Solids class 11:

All applicants preparing for entrance examinations such as JEE and NEET will benefit from the ncert solutions for class 11 physics chapter 9. Mechanical properties of solids notes, are particularly useful for revision when you are short on time and have a lot of material to cover. Every year, they have posted at least two questions from properties of solids and liquids, as has been the case over the past five years. This is one of the most important chapters on the syllabus. So, if you have enough time, tackle solids before fluids because solids introduce us to new concepts such as stress, strain, potential energy, and strain relation. These subjects aren't as important in fluids, but you should start with solids since if you miss a chapter in the middle, you'll end up with a backlog. one must practice all mechanical properties of solids neet questions and furthermore, one should also practice with mechanical properties of solids class 11 questions and answers pdf. Also to prepare the best one must refer to ncert solutions for class 11 physics chapter 9 and class 11 mechanical properties of solids notes combined.

If you have time constraints, then also you should do solids first as it is a small chapter which will not take much time of yours!

NCERT Solutions Subject wise link:

• NCERT solutions for class 11 Physics.
• NCERT solutions for class 11 Chemistry.
• NCERT solutions for class 11 Mathematics.
• NCERT solutions for class 11 Biology.

NCERT Exemplar Solutions Subject wise link:

• NCERT exemplar solutions for class 11 Physics.
• NCERT exemplar solutions for class 11 Chemistry.
• NCERT exemplar solutions for class 11 Mathematics.
• NCERT exemplar solutions for class 11 Biology.