Relation Between Volumetric Strain, Lateral Strain And Poisson’s Ratio

The volumetric strain, lateral strain, and Poisson's ratio relationship form a basis that has to be understood to get an insight into material deformation behaviour under stress. For instance, rubber balls deformed by squeezing, or metal pieces strained along one axis will not change only in the direction of the force applied but also along the perpendicular directions. The interaction entered in these cases is measured through Poisson's ratio, a factor that relates the lateral and axial strains of a material. Such relationships empower us to create structures that are safe and efficient, everything from skyscrapers and bridges down to simple plastic containers and metal rods.

In this article, we will cover the concept of the relation between volumetric strain, Lateral Strain And Poisson’s Ratio. This concept we study in Properties of Solids and Liquids which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of three questions have been asked on this concept. But no direct question was found in NEET.

Relation Between Volumetric Strain, Lateral Strain And Poisson’s Ratio

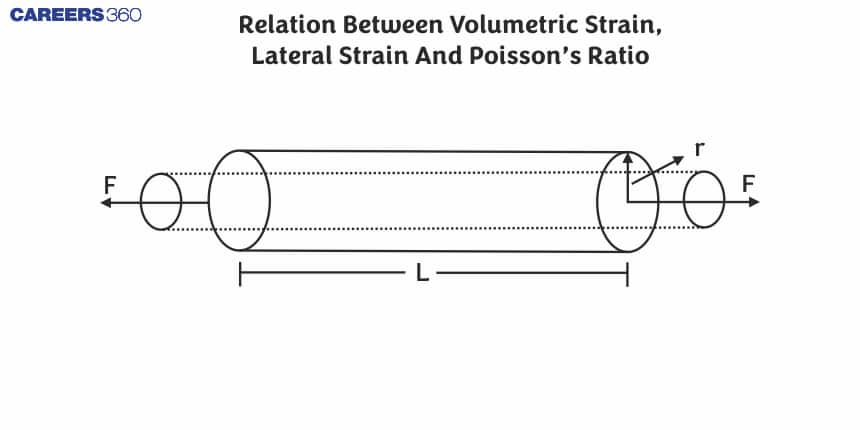
Let us long rod have a length L and radius 'r', then the volume of this rod = \pi $r^{2}L\dots \dots \dots \text{(1)}$

Now, Differentiating both the sides of equation (1), we get

$dV=\pi r^{2}dL+\pi 2rLdr$

Now, dividing both the sides by volume of the rod, i.e., $\pi r^{2}L$, we get,

$\frac{dV}{V}=\frac{\pi r^{2}dL}{\pi r^{2}L}+\frac{\pi 2rLdr}{\pi r^{2}L}=\frac{dL}{L}+2\frac{dr}{r}\dots (2)$

So we can say that,

Volumetric strain = Longitudinal strain + 2(Lateral strain)

Also, equation (2) can be written as,

$\Rightarrow \frac{dV}{V}=\frac{dL}{L}-2\sigma \frac{dL}{L}=(1-2\sigma )\frac{dL}{L}$

This is because, $[\sigma =\frac{-dr/r}{dL/L}\Rightarrow \frac{dr}{r}=-\sigma \frac{dL}{L}]$

Special Case

Now, let's see some special cases which are given below:

• $\text{When}\sigma =0.5\text{, then}dV=0\text{.}$ It means that the substance is incompressible, so there is no change in volume.
• If a material having $\sigma =0$, it means the lateral strain is zero. So, when a substance is stretched its length increases without any decrease in diameter. For example - cork has $\sigma =0$. Also, in this case, change in volume is maximum.

Recommended Topic Video

Solved Example Based on Relation Between Volumetric Strain, Lateral Strain And Poisson’s Ratio

Example 1: If $\mathrm{Y},\mathrm{K}$ and $\eta$ are the values of Young's modulus, bulk modulus and modulus of rigidity of any material respectively. Choose the correct relation for these parameters.

1) ${}^{\eta }=\frac{3YK}{9K+Y}N/m^2$
2) $Y=\frac{9K\eta }{2\eta +3K}N/m^2$
3) $K=\frac{Y\eta }{9\eta -3Y}N/m^2$
4) $Y=\frac{9K\eta }{3K-\eta }N/m^2$

Solution:

Let $\alpha =$ longitudinal strain per unit stress $=\frac{\mathrm{\Delta }l}{l}$
And $\beta =$ lateral strain per unit stress. $=\frac{\mathrm{\Delta }d}{d}$
Then Poisson's ratio, $\sigma =\frac{\text{lateral strain}}{\text{longitudinal strain}}=\frac{\beta }{\alpha }$
Young's modulus, $Y=\frac{\text{longitudinal stress}}{\text{longitudinal strain}}=\frac{1}{\frac{\text{longitudinal stress}}{\text{longitudinal strain}}}=\frac{1}{\alpha }$
And Bulk modulus, $K=\frac{\text{hydrostatic strain}}{\text{volumetric strain}}=\frac{1}{3(\alpha -2\beta )}$

$K=\frac{1}{3(\alpha -2\beta )}=\frac{1}{3\alpha (1-2\frac{\beta }{\alpha })}$

Since $\sigma =\frac{\beta }{\alpha }$ and $Y=\frac{1}{\alpha }$, so by substituting these values in above equation, we get
$K=\frac{Y}{3(1-2\sigma )}\cdots \cdots \cdot (1)$

Now the options are given in terms of $\mathrm{Y},\mathrm{K}$ and modulus of rigidity $(\eta )$.
For this we can use this formula
$Y=2\eta (1+\sigma )\cdots \cdots \cdot (2)$

From equation( 1)
$\begin{array}{rl}& 1-2\sigma =\frac{Y}{3K}\\ & \Rightarrow 2\sigma =1-\frac{Y}{3K}\\ & \Rightarrow \sigma =\frac{1}{2}(1-\frac{Y}{3K})\cdots \cdots (3)\end{array}$

Now from equation (2)
$\sigma =\frac{Y}{2\eta }-1\cdots \dots$

By comparing equations (3) and (4), we have
$\begin{array}{rl}& \frac{1}{2}(1-\frac{Y}{3K})=\frac{Y}{2\eta }-1\\ & \Rightarrow \frac{3}{2}-\frac{Y}{6K}=\frac{Y}{2\eta }\\ & \Rightarrow 3-\frac{Y}{3K}=\frac{Y}{\eta }\end{array}$

n further solving, we get
$\begin{array}{rl}& 3=\frac{Y}{\eta }+\frac{Y}{3K}\\ & \Rightarrow \frac{Y}{3K}=3-\frac{Y}{\eta }\\ & \Rightarrow \frac{Y}{3K}=\frac{3\eta -Y}{\eta }\\ & \Rightarrow K=\frac{Y\eta }{9\eta -3Y}\end{array}$

Hence, the answer is option (3).

Example 2: A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of the area floats on the surface of the liquid, covering the entire cross-section of the cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, $\left(\frac{dr}{r}\right)$ is:

1) $\frac{mg}{Ka}$
2) $\frac{Ka}{mg}$
3) $\frac{Ka}{3mg}$
4) $\frac{-mg}{3Ka}$

Solution:

Bulk Modulus -

The ratio of normal stress to volumetric strain.

$\begin{array}{rl}& K=\frac{f/A}{-\mathrm{\Delta }v/v}=\frac{-Fv}{A\mathrm{\Delta }v}\\ & K=\frac{-Pv}{\mathrm{\Delta }v}\end{array}$

v = Original volume

$\mathrm{\Delta }v=\text{Change in volume}$

P = Increase in pressure

$\text{-ve(sign) shows volume}(\mathrm{\Delta }v)\text{decrease.}$

- wherein

$\begin{array}{ll}\mathrm{\Delta }P=\frac{mg}{a}& V=\frac{4\pi }{3}{r}^3\\ K=-\frac{\mathrm{\Delta }P}{\left(\frac{\mathrm{\Delta }V}{V}\right)}& \therefore \frac{dV}{V}=3\cdot \frac{dr}{r}\\ K=\frac{-\mathrm{\Delta }P}{3\cdot \left(\frac{dr}{r}\right)}& \\ \text{or}\frac{dr}{r}=\frac{-mg}{3Ka}& \end{array}$

Hence, the answer is option (4).

Example 3: A material has Poisson's ratio of 0.5. If a uniform rod of it suffers a longitudinal strain of $2\times {10}^{-3}$. The percentage change in its volume is:

1) $5\mathrm{\%}$
2) $10\mathrm{\%}$
3) $12\mathrm{\%}$
4) $0\mathrm{\%}$

Solution:

Use,

$\begin{array}{rl}\frac{\mathrm{\Delta }V}{V}\times 100& =\frac{\mathrm{\Delta }l}{l}(1-2\sigma )\\ & =\frac{\mathrm{\Delta }l}{l}(1-2\times 0.5)\\ & =\frac{\mathrm{\Delta }l}{l}(1-1)=0\mathrm{\%}\end{array}$

Hence, the answer is option (4).

Example 4: Choose the correct relationship between the Poisson ratio $(\sigma )$and bull modulus (k) of rigidity $(\eta )$ of a given solid object :

1) $\sigma =\frac{3K+2\eta }{6K+2\eta }$
2) $\sigma =\frac{3K-2\eta }{6K+2\eta }$
3) $\sigma =\frac{6K+2\eta }{3K-2\eta }$
4) $\sigma =\frac{6K-2\eta }{3K-2\eta }$

Solution:

$\begin{array}{ll}Y=2\eta [1+\sigma ]& \\ \text{and}& Y=3K[1-2\sigma ]\\ \text{Now}& 2\eta (1+\sigma )=3K(1-2\sigma )\\ & 2\eta \sigma +2\eta =3K-6K\sigma \\ & (2n+6K)\sigma =3K-2n\\ & \sigma =\frac{3K-2n}{2\eta +6K}\end{array}$

Hence, the answer is option (2).

Example 5: A solid sphere of radius R made of material of buck modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area A floats on the surface of the liquid when a mass m is placed on the piston to compress the liquid, the fractional change in the radius of the sphere $\frac{\mathrm{\Delta }R}{R}$ is _____.

1) $\frac{mg}{AK}$
2) $\frac{mg}{3AK}$
3) $\frac{mg}{A}$
4) $\frac{3mg}{AK}$

Solution:

$\mathrm{\Delta }P=\frac{mg}{A}$

Volumetric strain is
$\begin{array}{rl}\frac{\mathrm{\Delta }V}{V}& =\frac{\mathrm{\Delta }P}{K}\\ 3\frac{\mathrm{\Delta }R}{R}& =\frac{mg/A}{K}\\ \frac{\mathrm{\Delta }R}{R}& =\frac{mg}{3KA}\end{array}$

Hence, the answer is option (2).

Summary

Volumetric strain is a measure of volume changes of a material under stress. Lateral strain is a measure of deformation perpendicular to the applied force. The ratio of lateral to axial strains is Poisson's ratio. All of these concepts are connected by the fact that Poisson's ratio makes predictions for the lateral and volumetric changes a material will undergo upon stretching or compressing.