Optical Density - Formula, FAQs

Q: Define optical density.

Optical density of a medium tells us about the ability of that medium to which extent or to which angle it can bend an incident ray of refraction.

Q: How absorbance and transmittance are related to each other?

Absorbance and transmittance are inversely proportional to each other.

Q: Why can transmittance never be greater than 1?

Transmittance greater than 1 means that somehow more light left the solution than entering, which is impossible.

Q: Mention the unit of measuring absorption of light.

Absorbance units measure how much light a particular wavelength is absorbed.

Q: Write the optical density formula and write optical density units.

Optical density is given by, Log(1/T)where, T is transmittance. optical density is a unitless quantity.

Optical Density - Formula, FAQs

Edited By Team Careers360 | Updated on Nov 12, 2024 09:24 PM IST

Introduction:

Optical density meaning is the change in the percentage transmission of light. Optical density meaning in Hindi is ऑप्टिकल घनत्व. In this article we will study in detail about what do you mean by optical density, what is absorbance, what is transmittance and what is high optical density.

Optical density:

Let us study optical density. Optical density definition can be given as the ability of that medium to which extent or to which angle it can bend an incident ray of refraction. In other words Optical density is the ability of a medium to refract a light or the degree to which a refractive medium bends an incident ray.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Introduction:
Optical density:
What does the 2.4 refractive index of the diamond mean?

Optical Density - Formula, FAQs

Optical density is not the same as mass density or physical density. Like mass density is calculated by mass and volume but optical density cannot be calculated like this.

Based on optical density we can divide the medium into two categories which is denser medium and Rarer medium.

Let us discuss what is a denser medium and rarer medium. In denser medium the speed of light decreases whereas in rarer medium speed of light is high.

NCERT Physics Notes:

In denser medium:

as the light comes from air to water (Rarer to denser medium) its speed decreases and that is why it bends towards normal.

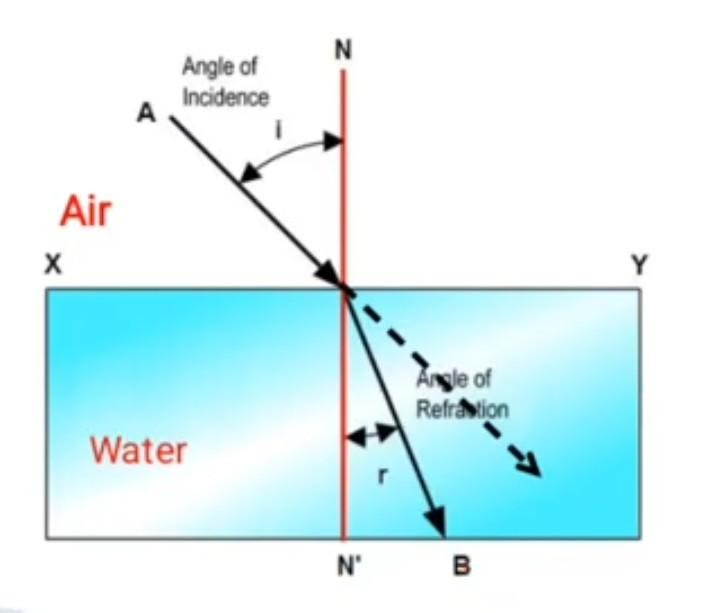
The ray is incident on a surface which is separating air and water. First, the incident light is coming from air, falls on the surface and then travels to water. The dotted line indicates the incident path but after refraction it follows another path. We can see that the ray bends towards the normal after refraction. This is because the air is optically rarer medium and water is optically denser medium. So, as the light comes from air to water (Rarer to denser medium) its speed decreases and that is why it bends towards normal.

Also read -

In Rarer medium:

as the incident ray cross water and travels into air it's speed increases that is why the incident ray moves away from normal.

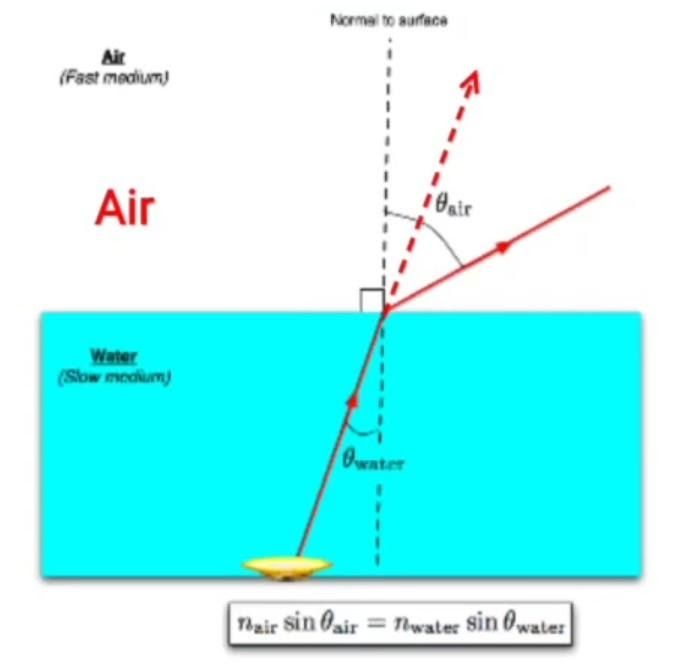
In this example, a bulb is placed inside the water. So the incident ray will be within the water. The incident ray falls on the surface coming from water and travels into air. After refraction it bends away from normal. It is because, as the incident ray crosses water and travels into air its speed increases that is why the incident ray moves away from normal.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Refractive index:

Based on what is optical density in physics, we can explain the refractive index. They are one or the same thing, they are like two faces of the same coin. An optically denser medium will have a high refractive Index. So if we compare water and air. Water is optically denser medium in comparison to air. So, water will have a high refractive Index.

Refractive index is represented by or n

Refractive index is defined as the ratio of the speed of light in a vacuum to the speed of light in a particular medium.

Mathematically,

μ=speed of light in vacuum / speed of light in a medium

Or, μ=c/v

This value is also known as absolute Refractive Index.

From above we can say that the Refractive index is inversely proportional to the velocity of light in a medium.

Refractive Index is a unit less quantity. It is because the refractive index is a ratio between two similar quantities.

Also, when the refractive index is greater the medium is optically denser and the speed of light in it will be slow. Similarly when the refractive Index is smaller the medium is less optically denser and the speed of lights in it will be high.

This was all about the optical density and refractive index. To understand it better let us look at the following numerical problem.

Numeral Problem

The speed of light in a diamond is 1.25 x10⁸ m/s. find the absolute refractive Index?

We know,

ray of light travelling from vacuum to diamond.

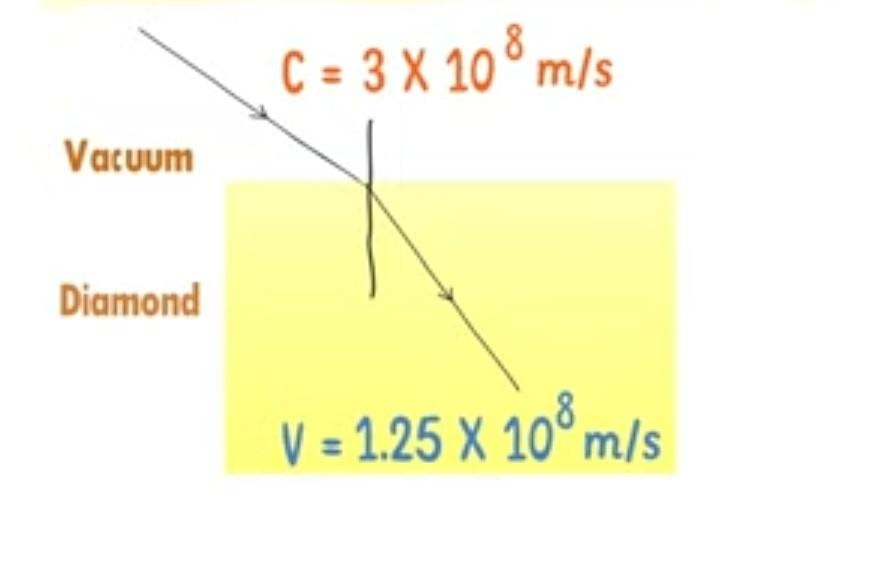
Refractive index = μ=speed of light in vacuum / speed of light in a medium= c/v

Where c = 3 x 10⁸m/s and v = 1.25 x 10⁸ m/s
so,

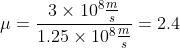
$\mu=\frac{3\times10^8\frac{m}{s}}{1.25\times10^8\frac{m}{s}}=2.4$

Also read :

What does the 2.4 refractive index of the diamond mean?

It means that the speed of light is 2.4 times slower in the diamond than the speed of light in the vacuum.

NOTE: Refractive Index is always greater than 1. It is because in the case of absolute Refractive Index light always travels from the vacuum (Rarer medium) to the denser medium (like water, glass etc.). So the speed of light always slows down in the denser medium and absolute refractive index is therefore always greater than 1.

Transmittance:

Let us define transmittance. When light passes through a solution some light gets absorbed by the solution and some light passes right through. To quantify the amount of light that passes through or transmitted through a solution, we use transmittance. Light of a particular wavelength that enters a solution has a certain intensity. We call this intensity the intensity of incident light and is denoted by I₀ . As light passes through the sample, some light might get absorbed and we can know the intensity of transmitted light that is I. The transmittance is simply a ratio of the transmitted Intensity over the intensity of incident light and because it's a ratio it does not have any unit. Transmittance is denoted by T.

Transmittance formula, T = I/I₀

As intensity of transmitted light is much smaller than intensity of incident light therefore the transmittance is low (T<<1). If a solution does not absorb any light then the intensity of transmitted light is equal to the Intensity of Incident light. Thus, the transmittance is equal to 1(T=1). Transmittance can never be greater than 1. Transmittance greater than 1 means that somehow more light left the solution than entering, which is impossible.

Absorbance:

Let us define absorbance. The absorbance meaning/absorbance definition is given as a measure of how much light a particular wavelength is absorbed. It equals the negative log of transmittance. So it is inversely proportional to the transmittance. As transmittance increases the negative log of the transmittance increases hence absorbance decreases. Absorbance symbol is denoted by A.

Absorbance formula, A = - (log T)

There is no SI unit of absorbance, absorbance is unit less.

Also check-

Frequently Asked Questions (FAQs)

1. Define optical density.

Optical density of a medium tells us about the ability of that medium to which extent or to which angle it can bend an incident ray of refraction.

2. Why is the refractive index always greater than 1?

It is because in the case of absolute Refractive Index light always travels from the vacuum (Rarer medium) to the denser medium (like water, glass etc.). So the speed of light always slows down in the denser medium and absolute refractive index is therefore always greater than 1.

3. Why is the refractive index dimensionless?

It is because the refractive index is a ratio between two similar quantities.

4. How absorbance and transmittance are related to each other?

Absorbance and transmittance are inversely proportional to each other.

5. Why can transmittance never be greater than 1?

Transmittance greater than 1 means that somehow more light left the solution than entering, which is impossible.

6. Mention the unit of measuring absorption of light.

Absorbance units measure how much light a particular wavelength is absorbed.

7. Write the optical density formula and write optical density units.

Optical density is given by, Log(1/T)where, T is transmittance.

optical density is a unitless quantity.