Real Gas And Equation

A true gas is one that defies gas laws under all typical pressure and temperature conditions. As the gas gets massive and voluminous, it starts to behave differently from how it should. Real gases have mass, volume, and velocity. When cooled to their boiling point, they liquefy. When compared to the overall amount of gas, the space used by gas is not modest.

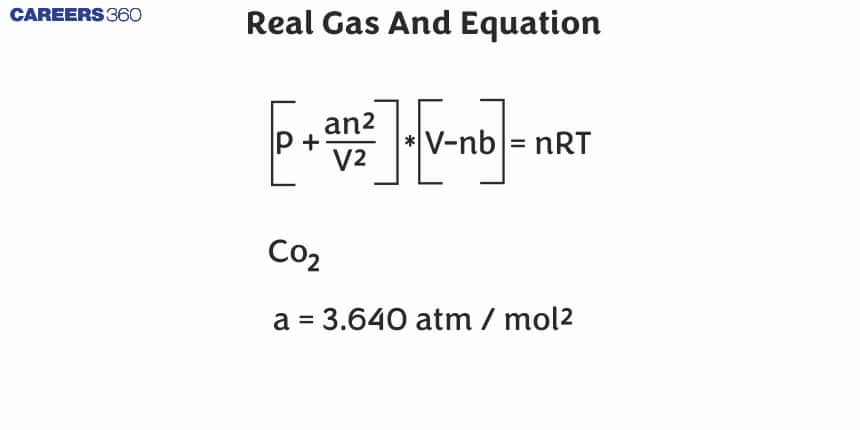
In this article, we will cover the concept of the real gas equation. This is one of the important concepts in the chapter Kinetic Theory of Gases. It is not only important for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE and more. In the last ten years of JEE Main and NEET, no direct questions were asked.

What is Real Gas?

Real gas: The gases which do not obey gas Laws are called Real gas.

Two main factors because of which Real gas deviates from ideal gas are:

1) Presence of force of attraction between molecules.

2) The size of molecules is not negligible.

The gases actually found in nature are called real gases.

From the ideal gas equation, we get

For exactly one mole of an ideal gas PVRT=1

The quantity PVRT is called the compressibility factor and should be a unit for an ideal gas.

Plotting the experimentally determined value of PVRT for exactly one mole of various real gases as a function of pressure P shows a deviation from identity as shown in the below graph.

Similarly, real gases show deviation from ideal behaviour as a function of temperature as shown in the below graph.

From the above graphs, we can say that A real gas behaves as an ideal gas most closely at low pressure and high temperature.

Real Gas Equation

The real gas equation, For n moles of gas, is given by

(P+n2aV2)(V−nb)=nRT....... (1)

Where a and b are called Vander wall's constant having dimensions and units as follows:

Dimension : [a]=[ML5T−2] and [b]=[L3]
Units : a=N×m and b=m3
Dimension : [a]=[ML5T−2] and [b]=[L3]
Units : a=N×m and b=m3

As we know the ideal gas equation is PV=nRT...... (2)

From equations (1) and (2) we can say that

The real gas equation is nothing but the ideal gas equation with two corrections (i.e Volume correction and Pressure correction)

These corrections are given by Vander Waal's. So the real gas equation is also known as Vander Waal's gas equation.

• Volume correction- Due to the finite size of the molecules the effective volume of gas becomes (V –nb).
• Pressure correction- Due to the presence of intermolecular force in real gases, the effective pressure of gas becomes P+n2aV2

For More Information On Real Gas And Equation, Watch The Below Video:

Solved Example Based on Real Gas And Equation

Example 1: For an oxygen molecule (molecular mass 32 g/mole ), the mass of a single molecule of O2 is P×10−24 gmolecules −1, then what is the value of P ?

1) 85.16

2) 53.14

3) 63.23

4) 38.29

Solution:

Avogadro's Number

NA=Mm

M = molecular mass of the compound

m = mass of single molecules

mO2=MNA=32 g mole−16.022×1023 molecular mole −1mO2=53.14×10−24 gmolecule−1

Hence, the answer is option (2).

Example 2: The compressibility factor for real gas can be -

1) Less than 0

2) Less than 1

3) More than 1

4) Both (2) and (3)

Solution:

We know pressure is inversely proportional to volume. So, if the pressure is high, then the volume will be low.

1. At high pressure, aV2 can be neglected.

PV−Pb=RTPVRT=1+PbRT

In this case, the compressibility factor is greater than 1.

2. At low pressure

If the pressure is low then the volume will be high, V>>b

Hence, the equation becomes-

(P+aV2)(V)=RT

Rearranging this equation, we get

PV=RT−aVPVRT=1−PbRT

In this case, the compressibility factor is less than 1.

So, the compressibility factor can be greater than or less than 1 for real gas

Hence, the answer is the option (4).

Example 3: For which of the following conditions is the law PV = RT obeyed most closely by a real gas,

1) High pressure and high temperature

2) High pressure and low temperature

3) low pressure and low temperature

4) Low-pressure and high-temperature

Solution:

Real gases deviate slightly from ideal gas law because of two main factors.

Two main factors are;

1) The force of attraction between molecules.

2) The size of molecules is not negligible.

And above two criteria will be fulfilled at low pressure and high temperature, and then the real gases behave like ideal gases.

Hence, the answer is the option (4).

Example 4: The equation of the state of a gas is given by P(V−b)=nRT. If 1 mole of a gas is isothermally expanded from volume V to 2 V, the work done during the process is:

1) RTln⁡|2V−bV−b|
2) RTln⁡|V−bV|
3) RTln⁡|V−b2V−b|
4) RTln⁡|VV−b|

Solution:

W=∫PdV=∫V2 VnRTV−bdV=RTln⁡|2 V−bV−b|

Hence, the answer is the option (1).

Summary

In order to determine the velocity and volume of the gas molecules, the general kinetic theory of gases treats the molecules as particles. According to this hypothesis, when gas molecules collide with a container's surface or with each other, the pressure inside the gas molecules rises. This theory is used to assess and determine a number of gas properties.