Reflection And Transmission Of Waves On A String

Edited By Vishal kumar | Updated on Jul 02, 2025 06:19 PM IST

When a wave travels along a string, its behaviour changes when it encounters a boundary or an obstacle. This phenomenon, known as the reflection and transmission of waves on a string, is crucial for understanding wave mechanics. Imagine plucking a guitar string: the vibrations you see are waves travelling back and forth along the string. When these waves hit the ends of the string, they either reflect back or transmit energy into another medium, like the body of the guitar, producing sound. In real life, similar principles apply to seismic waves during an earthquake, where waves reflect and transmit through different layers of the Earth, influencing the magnitude and impact of the quake. In this article, we will understand these wave behaviours not only deepens our grasp of physics but also has practical implications in engineering, music, and geology.

This Story also Contains

Reflection and Transmission of Waves on a String
Boundary Conditions
Assuming no transmission, no absorption and energy lost when a wave hits the boundary.
Wave in a Combination of String
Solved Examples Based on Reflection and Transmission of Waves on a String
Summary

Reflection And Transmission Of Waves On A String

Reflection and Transmission of Waves on a String

When a wave travels along a string and encounters a point of discontinuity, such as a change in the string's thickness or tension, it undergoes reflection and transmission. In simpler terms, part of the wave's energy is reflected back along the string, while the rest continues to travel through the new medium. This process is akin to what happens when you pluck a guitar string: the vibrations, or waves, move along the string, reflect at the ends, and transmit energy to produce sound. When waves are incident on a boundary between two media a part of incident waves returns back into the initial medium ( reflection ) while the remaining is partly absorbed and partly transmitted into the second medium ( refraction ).

Boundary Conditions

Assuming no transmission, no absorption and energy lost when a wave hits the boundary.

1. Rigid end

when the incident wave reaches a fixed end, it exerts an upward pull on the end, according to Newton's 3rd law at a fixed end it exerts an equal and opposite downward force on the string. It results in an inverted pulse or phase change of $π$ .

Crest (C) reflects as a trough(T) and vice-versa, Time changes by $\frac{T}{2}$ and path changes by $\frac{λ}{2}$ .

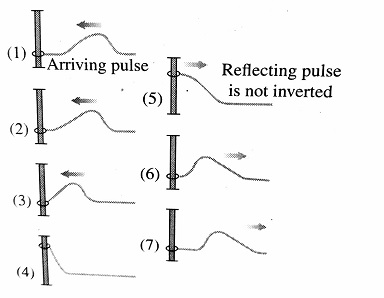
2) Free End

when a wave or pulse is reflected from a free end, then there is no change of phase (as there is no reaction force).

crest (C) reflects as the crest (C) and trough (T) reflects as a trough(T), Time changes by zero and path changes by zero.

Wave in a Combination of String

1. Wave goes from rarer to a denser medium

$\begin{aligned} Incident wave \Rightarrow y_{i} = a_{i} \sin (ω t - k_{1} x) \\ Reflected wave \Rightarrow y_{r} = a_{r} \sin [ω t - k_{1} (- x) + π] = - a_{i} \sin (ω t + k_{1} x) \\ Transmitted wave \Rightarrow y_{t} = a_{t} \sin (ω t - k_{2} x) \end{aligned}$

2. Wave goes from denser to rarer medium

$\begin{aligned} Incident wave \Rightarrow y_{i} = a_{i} \sin (ω t - k_{1} x) \\ Reflected wave \Rightarrow y_{r} = a_{r} \sin [ω t - k_{1} (- x) + 0] = a_{i} \sin (ω t + k_{1} x) \\ Transmitted wave \Rightarrow y_{t} = a_{t} \sin (ω t - k_{2} x) \end{aligned}$

The Amplitude of Reflected Wave

If $A_{r} =$ the amplitude of the reflected wave then
$A_{r} = \frac{(V_{2} - V_{1}) A_{i}}{(V_{2} + V_{1})}$

Where

$V_{1}$ and $V_{2}$ are the velocity of the wave in the incident and transmitted wave.
$A_{i} =$ the amplitude of the incident wave.
Or we can write $\frac{A_{r}}{A_{i}} = \frac{k_{1} - k_{2}}{k_{1} + k_{2}} = \frac{v_{2} - v_{1}}{v_{2} + v_{1}}$
Where $k_{1}$ and $k_{2}$ are the angular wave numbers of the incident and transmitted wave respectively.

Amplitude of transmitted wave

If the amplitude of the transmitted wave then

$A_{t} = (\frac{2 V_{2}}{V_{1} + V_{2}}) A_{i}$

Where
$V_{1}$ and $V_{2}$ are the velocity of the wave in the incident and transmitted wave.
$A_{i} =$ the amplitude of the incident wave.
Or we can write $\frac{A_{t}}{A_{i}} = \frac{2 k_{1}}{k_{1} + k_{2}} = \frac{2 v_{2}}{v_{2} + v_{1}}$
Where $k_{1}$ and $k_{2}$ are the angular wave numbers of the incident and transmitted wave respectively.

Solved Examples Based on Reflection and Transmission of Waves on a String

Example 1: A wave is reflected from a rigid support. The change in phase on reflection will be

1) $\frac{π}{4}$
2) $\frac{π}{2}$
3) $π$
4) $2 π$

Solution:

Reflection of wave-fixed end

1) There is a phase change for the reflected wave

2) At the boundary, some or all of the waves are reflected.

3) When it is reflected from a fixed end, the wave is inverted.

After reflection from rigid support, a wave suffers a phase change of $π$

Hence, the answer is the option (3).

Example 2: A string of length 20 cm and linear mass density 0.40 g/cm is fixed at both ends and kept under tension 16N. A pulse at t=0 near one end occurs while travelling towards the other end. When will it have the same shape (time in seconds)

1) 0.02

2) 2

3) 0.01

4) 0.4

Solution:

The velocity of the wave, $v = \sqrt{(T / m)} = \sqrt{(16 \times 10^{5}) / 0.4} = 2000 cm / \sec$

$\therefore$ Time taken to reach the other end =20 / 2000=0.01 sec

Total time is taken to see the pulse again in the original position =0.01 x 2=0.02 sec

Hence, the answer is the option (1).

Example 3: To decrease the fundamental frequency of stretched string at both ends one might

1) Increase Tension

2) Increase Wave velocity

3) Increase Length

4) Decrease Liner momentum

Solution:

Reflection of wave-free end

1) If the end of the string is free to move vertically, the free end overshoots twice the amplitude.

2) At the boundary all or part of it is reflected.

3) When reflected from the free end, the pulse is not inverted.

After increasing length freq. decreases

Hence, the answer is the option (3).

Example 4: What is the value of phase change when a transverse wave strikes the free end?

1) 0^o

2) 90^o

3) 180^o

4) 270^o

Solution:

When the incident wave reaches a free end, it exerts an upward pull on the free end as there is no opposition, the crest returns as a crest or trough return as a trough.

Hence, the answer is the option (1).

Example 5: What is the value of phase change when a transverse wave pulse is reflected by the free end?

1) 0^o

2) 90^o

3) 180^o

4) 270^o

Solution:

When a transverse wave or pulse is reflected from a free end, then there is no change of phase (as there is no reaction force).

Hence, the answer is the option (1).

Summary

The reflection and transmission of waves on a string occur when a wave encounters a boundary or discontinuity, leading to the division of energy between reflected and transmitted waves. The behaviour of these waves depends on the boundary conditions, such as whether the end is rigid or free. The amplitude and phase change of the reflected and transmitted waves are governed by the properties of the string and the medium it interacts with.

Frequently Asked Questions (FAQs)

1. How does the amplitude of a reflected wave compare to the incident wave?

In an ideal situation with no energy loss, the amplitude of the reflected wave equals that of the incident wave. However, in real-world scenarios, some energy is usually lost due to factors like friction or transfer to the reflecting surface, resulting in a slightly reduced amplitude.

2. What is meant by the "reflection coefficient" in wave mechanics?

The reflection coefficient is a measure of the fraction of wave amplitude or energy that is reflected at a boundary. It ranges from -1 to 1, where -1 indicates complete reflection with phase inversion, 0 indicates no reflection (complete transmission), and 1 indicates complete reflection without phase inversion. The value depends on the properties of the media on either side of the boundary.

3. What is the relationship between wave reflection and energy conservation?

The principle of energy conservation applies to wave reflection. In an ideal system, the total energy of the incident wave equals the sum of the energies of the reflected and transmitted waves. In reality, some energy may be lost to the surrounding environment or converted to other forms, but the principle of energy conservation still holds when all forms of energy are accounted for.

4. What is the difference between constructive and destructive interference in reflected waves?

Constructive interference occurs when the crests of two waves align, resulting in a larger amplitude. Destructive interference happens when a crest aligns with a trough, resulting in a smaller or zero amplitude. In reflected waves, these interference patterns can create standing waves with nodes (points of destructive interference) and antinodes (points of constructive interference).

5. How does the concept of nodes and antinodes relate to reflected waves on a string?

Nodes are points of minimum displacement in a standing wave pattern, while antinodes are points of maximum displacement. These patterns form when incident and reflected waves interfere. At nodes, the waves destructively interfere, while at antinodes, they constructively interfere. The positions of nodes and antinodes are determined by the wavelength and the boundary conditions of the string.

6. What determines whether a reflected wave is inverted or not?

The type of boundary determines whether a reflected wave is inverted. At a fixed end (like a wall), the wave is inverted upon reflection. At a free end (like a loose end of a string), the wave maintains its original shape. This is due to the boundary conditions imposed on the wave.

7. How do boundary conditions affect wave reflection on a string?

Boundary conditions determine how a wave behaves at the end of a string. A fixed end (like a wall) forces the displacement to be zero, causing the wave to invert upon reflection. A free end (like a loose end) allows maximum displacement, causing the wave to reflect without inversion. These conditions shape the reflected wave and influence the formation of standing waves.

8. What happens to a wave when it reaches the end of a string?

When a wave reaches the end of a string, it undergoes reflection. The wave bounces back, reversing its direction of travel. If the end is fixed, the reflected wave is inverted (upside-down). If the end is free, the reflected wave maintains its original shape.

9. What is the phase change in a wave reflected from a fixed end?

When a wave is reflected from a fixed end, it undergoes a 180-degree phase change, or a phase shift of π radians. This means the reflected wave is inverted compared to the incident wave. The reason is that the fixed end cannot move, forcing the wave to change direction and shape to satisfy this boundary condition.

10. What is meant by the term "impedance mismatch" in the context of wave reflection?

Impedance mismatch refers to the difference in the characteristic impedance of two media. In strings, this is related to differences in density and tension. When a wave encounters a boundary with an impedance mismatch, part of it is reflected. The greater the mismatch, the more energy is reflected rather than transmitted.

11. What is the difference between transmission and reflection of waves on a string?

Reflection occurs when a wave bounces back from a boundary, changing direction. Transmission happens when a wave passes through a boundary between two media (e.g., from one string to another). In transmission, the wave continues in its original direction but may change speed or amplitude.

12. How does the frequency of a wave change upon reflection or transmission?

The frequency of a wave remains constant during both reflection and transmission. This is because frequency is determined by the source of the wave, not the medium through which it travels. However, other properties like wavelength and speed can change when a wave is transmitted to a new medium.

13. How does the tension in a string affect wave reflection?

Tension in a string doesn't directly affect the occurrence of reflection, but it does influence the speed of the wave. Higher tension increases wave speed, which can change the timing of reflections. The fundamental principle of reflection remains the same regardless of tension.

14. How does the angle of incidence relate to the angle of reflection for waves on a string?

Unlike light waves, waves on a string are constrained to move along the string. Therefore, the concept of angle of incidence and reflection doesn't apply in the same way. The reflected wave simply travels back along the same path as the incident wave, but in the opposite direction.

15. How does the concept of wave impedance relate to reflection and transmission?

Wave impedance is a property of the medium that relates to how easily a wave can propagate through it. When a wave encounters a boundary between media with different impedances, part of the wave is reflected and part is transmitted. The greater the difference in impedance, the more energy is reflected rather than transmitted.

16. Can a wave be both reflected and transmitted at the same time?

Yes, when a wave encounters a boundary between two media (like two connected strings), part of the wave energy is reflected back, and part is transmitted through. The relative amounts of reflection and transmission depend on the properties of the two media.

17. What is a standing wave, and how is it related to reflection?

A standing wave is a pattern formed when two waves of the same frequency traveling in opposite directions interfere. It's often created by the superposition of an incident wave and its reflection. Standing waves appear stationary, with fixed points of no motion (nodes) and maximum motion (antinodes).

18. How does the density of a string affect wave transmission and reflection?

The density of a string affects the wave speed, which in turn influences transmission and reflection. A denser string results in slower wave speed. When a wave encounters a boundary between strings of different densities, part of it is reflected and part transmitted. The amount of reflection versus transmission depends on the difference in densities (and thus wave speeds) between the two strings.

19. What is the relationship between wave reflection and resonance in a string?

Reflection plays a crucial role in creating resonance in a string. When the reflected waves interfere constructively with the incident waves, standing waves form. Resonance occurs when the frequency of the driving force matches one of the natural frequencies of the string, determined by its length, tension, and density. This results in maximum amplitude of vibration.

20. How does the wavelength of a transmitted wave change when it enters a different medium?

When a wave is transmitted from one medium to another, its frequency remains constant, but its wavelength changes. If the wave speed decreases in the new medium, the wavelength becomes shorter. If the wave speed increases, the wavelength becomes longer. This relationship is described by the equation: wave speed = frequency × wavelength.

21. What is the significance of the "critical angle" in the context of wave reflection on strings?

The concept of a "critical angle" is more commonly associated with waves in two or three dimensions, like light waves

22. What is the superposition principle, and how does it apply to reflected waves?

The superposition principle states that when two or more waves overlap, the resulting displacement at any point is the sum of the displacements of the individual waves. This principle applies to reflected waves when they interfere with incident waves, creating patterns like standing waves.

23. How does the phase of a wave change when it is transmitted from one string to another?

When a wave is transmitted from one string to another, there may be a phase change depending on the properties of the two strings. If the second string has a higher wave speed (due to higher tension or lower density), the transmitted wave will have a phase advance. If the second string has a lower wave speed, there will be a phase delay. The magnitude of this phase change depends on the difference in wave speeds between the two strings.

24. What is the significance of the "characteristic impedance" of a string in wave reflection and transmission?

The characteristic impedance of a string is a property that depends on its tension and linear density. It determines how easily waves can propagate through the string. When a wave encounters a boundary between strings with different characteristic impedances, part of the wave is reflected and part is transmitted. The greater the difference in characteristic impedances, the more energy is reflected rather than transmitted.

25. How do multiple reflections affect wave behavior on a finite string?

On a finite string, waves can undergo multiple reflections from both ends. These reflections interfere with each other and with the incident waves, creating complex patterns. Under certain conditions, this can lead to the formation of standing waves. The interference of multiple reflections can also result in phenomena like beats or wave packets, depending on the frequencies and phases of the waves involved.

26. What is the relationship between wave reflection and the concept of "impedance matching"?

Impedance matching is the practice of making the impedance of a wave source equal to the impedance of the medium it's connected to. When impedances are matched, maximum energy transfer occurs, and reflection is minimized. In the context of strings, this could involve adjusting the tension or density of connected strings to ensure smooth wave transmission with minimal reflection at the boundary.

27. How does the amplitude of a transmitted wave compare to that of the incident wave?

The amplitude of a transmitted wave is generally different from that of the incident wave. The relationship depends on the properties of the two media (like the tension and density of the strings). If the second medium allows for easier wave propagation, the transmitted wave may have a larger amplitude. Conversely, if the second medium impedes wave motion, the transmitted amplitude will be smaller. The exact relationship is determined by the transmission coefficient, which depends on the impedance mismatch between the media.

28. What is the effect of damping on wave reflection and transmission?

Damping reduces the amplitude of waves over time and distance. In the context of reflection and transmission, damping can decrease the amplitude of both reflected and transmitted waves. It also affects the formation of standing waves, as the reflected waves have lower amplitude due to energy loss. In heavily damped systems, reflections may become negligible over time, and transmitted waves may quickly die out.

29. How do harmonics relate to wave reflection on a string?

Harmonics are the natural frequencies at which a string vibrates when it forms standing waves. These standing waves result from the constructive interference of incident and reflected waves. The fundamental frequency (first harmonic) and its integer multiples (higher harmonics) depend on the string's length, tension, and density. The reflection of waves at the string's ends is crucial for establishing these harmonic patterns.

30. What is the difference between partial reflection and total reflection?

Partial reflection occurs when some of the wave energy is reflected and some is transmitted at a boundary. This is common when a wave encounters a change in medium properties (like tension or density in strings). Total reflection occurs when all of the wave energy is reflected back into the original medium. In strings, this can happen at a free end or when there's an extreme mismatch in impedance between two connected strings.

31. How does the concept of wave packets relate to reflection and transmission?

A wave packet is a localized group of waves with different frequencies. When a wave packet encounters a boundary, its behavior depends on how each of its component frequencies reflects or transmits. This can lead to interesting phenomena like dispersion, where different frequencies reflect or transmit differently, potentially changing the shape of the wave packet. The reflection and transmission of wave packets can be more complex than that of simple harmonic waves.

32. What is the role of boundary conditions in determining the modes of vibration of a string?

Boundary conditions, such as fixed or free ends, determine the possible standing wave patterns (modes of vibration) on a string. These conditions dictate where nodes (points of no displacement) must occur. For example, a string fixed at both ends must have nodes at those points, limiting the possible wavelengths and frequencies of standing waves. The boundary conditions thus play a crucial role in determining the natural frequencies or harmonics of the string.

33. How does the concept of wave impedance relate to power transmission in waves?

Wave impedance is closely related to power transmission in waves. When a wave encounters a boundary between media with different impedances, the amount of power transmitted versus reflected depends on the impedance mismatch. Maximum power transmission occurs when the impedances are matched. This principle is important in various applications, from musical instruments to electrical signal transmission.

34. What is meant by the term "wave reflection coefficient" and how is it calculated?

The wave reflection coefficient is a measure of the fraction of wave amplitude that is reflected at a boundary. It's calculated as the ratio of the reflected wave amplitude to the incident wave amplitude. The reflection coefficient can be positive or negative, indicating whether the reflected wave is in phase or out of phase with the incident wave. It's determined by the impedance mismatch between the two media and ranges from -1 to 1.

35. How does the phase velocity of a wave change during transmission between two strings?

The phase velocity of a wave (the speed at which a particular phase of the wave travels) can change when the wave is transmitted from one string to another. If the second string has different properties (like tension or density), the phase velocity will change accordingly. The relationship is given by v = √(T/μ), where v is the phase velocity, T is the tension, and μ is the linear density of the string.

36. What is the significance of the transmission coefficient in wave mechanics?

The transmission coefficient is a measure of the fraction of wave amplitude or energy that is transmitted across a boundary. It complements the reflection coefficient, and together they describe how wave energy is distributed when a wave encounters a boundary. The transmission coefficient is important for understanding energy transfer between media and is crucial in applications ranging from acoustics to fiber optics.

37. How do reflected waves contribute to the formation of normal modes in a string?

Normal modes are the patterns of vibration in which all parts of the string move sinusoidally with the same frequency. These modes result from the constructive interference of incident and reflected waves. The reflected waves from both ends of the string must interfere in such a way that they reinforce each other, creating a standing wave pattern. The frequencies at which this occurs are the natural frequencies of the string, determined by its length, tension, and density.

38. What is the relationship between wave reflection and the concept of resonance in strings?

Resonance in strings occurs when the frequency of an applied force matches one of the string's natural frequencies. This is intimately related to wave reflection because the natural frequencies are determined by the constructive interference of reflected waves. When the incident waves have a frequency that allows their reflections to perfectly reinforce the motion, resonance occurs, resulting in maximum amplitude of vibration.

39. How does the concept of group velocity apply to reflected and transmitted waves?

Group velocity is the velocity at which the overall shape of a wave's amplitudes propagates through space. In the context of reflection and transmission, the group velocity can change when waves pass from one medium to another. While the frequency remains constant, changes in the medium's properties can alter the group velocity. This can lead to interesting effects, especially for wave packets, where the shape of the wave envelope may change upon reflection or transmission.

40. What is the effect of a gradual change in string properties on wave reflection and transmission?

A gradual change in string properties (like a gradual increase in density or tension) can lead to a phenomenon called impedance gradient. Unlike a sudden boundary, which causes clear reflection and transmission, a gradual change can result in a more continuous process of partial reflection and transmission along the gradient. This can lead to effects like wave bending or gradual changes in wave speed and amplitude.

41. How do reflected waves contribute to the concept of wave interference?

Reflected waves play a crucial role in wave interference. When an incident wave and its reflection overlap, they interfere according to the superposition principle. This interference can be constructive (amplifying the wave) or destructive (diminishing the wave), depending on the relative phases of the waves. The interference between incident and reflected waves is fundamental to the formation of standing waves and resonance patterns in strings.

42. What is the relationship between wave reflection and the concept of wave nodes?

Wave nodes are points of zero displacement in a standing wave pattern. They form at locations where incident and reflected waves consistently interfere destructively. In a string fixed at both ends, nodes always occur at the fixed points due to reflection. The spacing between nodes is related to the wavelength of the standing wave, which in turn depends on the frequency and the wave speed in the string.

43. How does the amplitude of a reflected wave compare to that of a transmitted wave at a boundary?

The relative amplitudes of reflected and transmitted waves at a boundary depend on the impedance mismatch between the two media. The sum of the energy in the reflected and transmitted waves equals the energy of the incident wave (assuming no energy loss). If there's a large impedance mismatch, more energy will be reflected, resulting in a larger reflected amplitude and a smaller transmitted amplitude. If the impedances are well-matched, more energy will be transmitted.