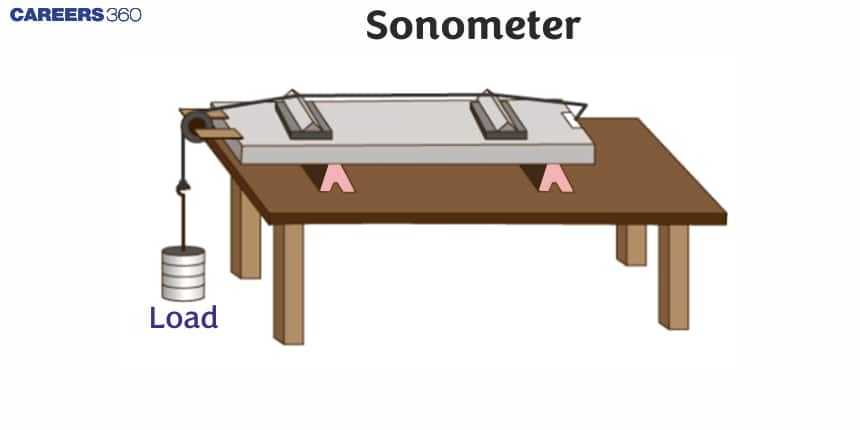
Sonometer

A sonometer is a device that people make use of in order to investigate how the string that actually creates them has any relationship with the physical attributes therein particularly relative to the frequency of sound waves. The frequency and wavelength of generated sound waves can be seen when one changes the tension, length and mass per unit length of the string. Therefore, in a sonometer oscillation of the string during vibrations causes waves of sound.

This Story also Contains

1. What is Sonometer And Its Principle
2. Solved Examples Based on Sonometer
3. Summary
4. Frequently Asked Questions (FAQs):

In this article, we will discuss how motion and sound use the sonometer as a critical instrument. The relevance of the sonometer is to the eleventh-grade and NEET, JEE Main topics as a matter of fact. It allows learners to see how frequency, tension and length relate to each other in a vibrating string while demonstrating the principles of sound waves and resonance. Over the last ten years of the JEE Main exam (from 2013 to 2023), four questions have been asked on this concept. And no direct question has been asked for the NEET exam on this concept.

What is Sonometer And Its Principle

It is a device used to measure the velocity of the transverse mechanical wave in a stretched metal wire.

The principle of sonometer is based on the resonance of string vibrations. Working oscillations are induced in a clamped string by an external source like a tuning fork or an oscillator and because of this, the amplitude becomes very high when resonance takes place.

There are two figures given below which show the setup of the Sonometer. There is a wooden box M on which wire AB is stretched by weight as shown in Figure (a). There are two clamps C₁ and C₂ which are ready to slide to change the length of the wire between the clamps.

Now we are placing an oscillating tuning fork in contact with the sonometer wire (See Figure (b)). When they get in touch, some oscillations are transferred to the wire. Let the tension in the wire is $\mathrm{T}\text{and}\mu$ is the mass per unit length of the wire. Also, the frequency of the tuning fork, then the wavelength of the wave in the wire is -

$\lambda =\frac{v}{n_0}=\frac{1}{n_0}\sqrt{\frac{T}{\mu }}$

If the length between clamps is an integral multiple of $\lambda /2$ then stationary waves are established in the portion of wire between $C_1\text{and}{C}_2$. To do this, Clamp $C_1$ is fixed and $C_2$ is displaced so that the oscillation amplitude of the wire is increasing and stationary waves are established. Let in this situation the length between clamps be $l$, now again $C_2$ is displaced away from $C_1$ so that again resonance is obtained. This will happen again when the clamp reaches the position $C_3$ and when the next node of stationary waves is present. Let this length be $l$, if $l_1$ and $l_2$ are two successive resonance lengths then we can write -

$\begin{array}{c}{l}_2-l_1=\frac{\lambda }{2}\\ \text{So,}\lambda =2(l_2-l_1)\end{array}$

If n_o is the frequency of oscillation, then the velocity of the string wave in wire--

$\begin{array}{rl}v& =n_0\lambda \\ & =2n_0(l_2-l_1)\end{array}$

This is partially measured velocity and we can compare this velocity with the formula

$\sqrt{\frac{T}{\mu }}$

Recommended Topic Video

Solved Examples Based on Sonometer

Example 1: The length of the sonometer wire AB is 110 cm. There are two bridges placed from A to B, and the wire is divided into 3 segments whose fundamental frequency is in ratio 1:2:3. What will be the ratio of their length?

1) (30, 40, 40) cm

2) (20, 80, 10) cm

3) (60,30, 20) cm

4) (10, 60, 40) cm

Solution:

Sonometer

It is a device used to measure the velocity of the transverse mechanical wave in a stretched wire.

wherein

The principle of a sonometer is based on the resonance of string vibration.

$\begin{array}{rl}& f\propto \frac{1}{l}\Rightarrow f_1:f_2:f_3=1:2:3\\ & l_1:l_2:l_3=\frac{1}{1}:\frac{1}{2}:\frac{1}{3}\\ & l_1:l_2:l_3=6:3:2\\ & l_1=\frac{6}{11}\times 110=60\mathrm{cm}\\ & l_2=\frac{3}{11}\times 110=30\mathrm{cm},\\ & l_3=\frac{2}{11}\times 110=20\mathrm{cm}\end{array}$

Hence, the answer is the option (3).

Example 2: When the string of a sonometer of length L between the bridges vibrates in the 2nd overtone, the amplitude of vibration is max at

1) $\left(\frac{L}{2}\right)$
2) $(\frac{L}{4},\frac{3L}{4})$
3) $(\frac{L}{6},\frac{3L}{6})$
4) $(\frac{L}{8},\frac{3L}{8})$

Solution:

The principle of sonometer is based on the resonance of string vibration.

$\frac{3\lambda }{2}=L\Rightarrow \lambda =\frac{2L}{3}$

Amplitude will be $\frac{L}{6},\frac{3L}{6},\frac{5L}{6}$ etc.

Hence, the answer is the option (3).

Example 3: Four wires of identical length, and diameters and of the same material are stretched on sonometer wire if the ratio of their tension is 1:4:9:16, then the ratio of their fundamental frequencies?

1) 16:9:4:1

2) 4:3:2:1

3) 1:4:2:16

4) 1:2:3:4

Solution:

$\begin{array}{rl}& \text{Fundamental freq.}=\frac{v}{2l}=\frac{\sqrt{\frac{T}{M}}}{2l}\Rightarrow f\propto \sqrt{T}\\ & f=\sqrt{1:4:9:16}\end{array}$

Hence, the answer is the option (4).

Example 4: Two wires W₁ and W₂ have the same radius r and respective densities ρ₁ and ρ₂ such that ρ₂= 4ρ₁. They are joined together at the point O, as shown in the figure. The combination is used as a sonometer wire and kept under tension T. The point O is midway between the two bridges. When a stationary wave is set up in the composite wire, the joint is found to be a node. The ratio of the number of antinodes formed in W₁ to W₂ is :

1) 1: 1

2) 1: 2

3) 1 : 3

4) 4: 1

Solution:

When the joint is found to be a node, then the frequency is given as

$n=\frac{p}{2l}\sqrt{\frac{T}{\pi r^{2}d}}$

Where p is also equal to the number of antinodes formed in the wire

As

$\begin{array}{rl}& n_1=n_2\\ & T\to \text{same}\\ & r\to \text{same}\\ & l\to \text{same}\end{array}$

So
$\begin{array}{rl}& \frac{p_1}{\sqrt{d_1}}=\frac{p_2}{\sqrt{d_2}}\\ & \frac{p_1}{p_2}=\frac{1}{2}\end{array}$

Hence, the answer is option (2).

Example 5: The fundamental frequency of the sonometer wire is n. If the tension is made three times and length and diameter are also increased by 3 times, what is the new frequency

1) $\frac{n}{3\sqrt{3}}$
2) $3n$
3) $\sqrt{3}n$
4) $\frac{n}{\sqrt{3}}$

Solution:

Standing wave in a string fixed at both ends

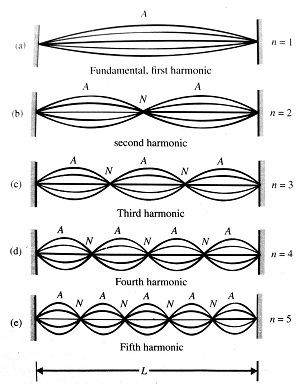
wherein

$\begin{array}{rl}& {\nu }_n=\frac{n}{2L}\cdot \sqrt{\frac{T}{\mu }}\\ & n=1,2,3\dots \dots \dots \dots \\ & {\nu }_n\text{frequency of nth harmonic.}\\ & T=\text{tension in string}\\ & \mu =\text{mass/length}\\ & n=\frac{1}{2l}\sqrt{\frac{T}{\mu }}=\frac{1}{2l}\sqrt{\frac{T}{\pi r^2\rho }}\\ & \Rightarrow n\propto \frac{\sqrt{T}}{l_r}\\ & \Rightarrow \frac{m_1}{n_2}=\sqrt{\frac{T_1}{T_2}}\times \frac{l_2}{l_1}\times \frac{r_2}{r_1}\\ & \Rightarrow \frac{n_1}{n_2}=\sqrt{\frac{T}{3T}}\times \frac{3l}{l}\times \frac{3r}{r}=3\sqrt{3}\\ & \Rightarrow n_2=\frac{n}{3\sqrt{3}}\end{array}$

$\text{So the new frequency will become}\frac{1}{3\sqrt{3}}\text{times}\text{of the initial frequency.}$

Hence, the answer is option (1).

Summary

A sonometer is a physics equipment used to do experiments on the principles of sound, vibrations and waves. Basically, it has a string stretched on a wooden box (resonator box) whose weight can be varied. The string vibrates and propagates sound waves whenever it is plucked. It should be noted at this juncture that the frequency of such vibrations depends on either the tension applied or its length.

Frequently Asked Questions (FAQs):

Q 1: What is the use of Sonometer?

Ans: It is a device used to measure the velocity of the transverse mechanical wave in a stretched metal wire.

Q 2: What is the principle of sonometer?

Ans: The principle of sonometer is based on the resonance of string vibrations. Working oscillations are induced in a clamped string by an external source like a tuning fork or an oscillator and because of this, the amplitude becomes very high when resonance takes place.

Q 3: What are the main components of a sonometer?

Ans: The main components of a sonometer are a hollow wooden box, a string, two fixed bridges, a movable bridge, and a set of weights for applying tension to the string.

Q 4: How does the length of the string affect the frequency of sound produced by a sonometer?

Ans: The frequency of the sound produced by a sonometer is inversely proportional to the length of the vibrating part of the string.