Staedy Conduction Heat Transfer

Steady conduction heat transfer refers to the consistent and uninterrupted flow of heat through a material or object, where the temperature difference remains constant over time. This process is governed by Fourier's Law, which states that the rate of heat transfer through a material is directly proportional to the temperature gradient and the material's thermal conductivity. In real life, steady conduction can be observed in various scenarios, such as the heat transfer through the walls of a home during winter. Here, the warmth inside attempts to escape to the colder exterior, but the insulation materials slow this process, ensuring a steady and manageable loss of heat. Understanding steady conduction is crucial in designing energy-efficient buildings, electronic devices, and thermal systems, where controlling heat flow is essential for performance and safety.

Steady Conduction Heat Transfer

In the previous heat transfer and its modes concept, we have learned the definition of Conduction. Now we will discuss the characteristics and properties of conduction.
(1) Heat flows from high temperature to low temperature. In this, the particles of the medium simply vibrate about their mean position but do not leave their place.
(2) Conduction heat transfer is medium-dependent.
(3) The temperature of the medium goes on increasing in the direction of heat transfer.
(4) Conduction mode of heat transfer is a process that is possible in all states of matter.
(5) In solids, the only mode of heat transfer is conduction.

(6) In metallic solids, free electrons carry the heat energy carrier, therefore they are good conductors of heat.

Terminologies Used in Steady State or Basics of Conduction

• Steady-state:It means that the temperature in the system is not time-dependent. So, if we supply heat to a body then the temperature of the body increases but after some time, a state is reached when the temperature of every cross-section of the body becomes constant. In this state, no heat is absorbed by the body. This state of the body is called a steady state.

• Isothermal surface: Any cross-section (within a conductor) having all its points at the same temperature, is called an isothermal surface.

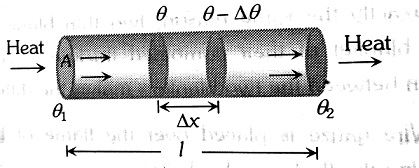
• Temperature gradient: The rate of change of temperature with distance between two isothermal surfaces is called temperature gradient. It is denoted by -

So,

Temperature gradient $=\frac{-\Delta \theta}{\Delta x}$
The negative sign shows that temperature $\theta$ decreases as the distance $x$ increases in the direction of heat flow.

• Thermal conductivity(K) - It is the measure of the ability of a substance to conduct heat through it. The magnitude of K depends only on the nature of the material. Substances which do not permit an easy flow of heat are called bad conductors. They possess low thermal conductivity due to very few freeelectrons.

Recommended Topic Video

Solved Examples Based on Steady Conduction Heat Transfer

Example 1: Thermal conductivity for a perfect conductor is

1) zero

2) infinite

3) Finite

4) All of the above

Solution:

Thermal Conductivity

$K=\infty$

wherein

For perfect conductor

Hence, the answer is the option (2).

Example 2: Two materials having coefficients of thermal conductivity $' 3 K^{\prime}$ and $' K^{\prime}$ and thickness ' d' and '3d', respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are $' \theta_2^{\prime}$ and ${ }^{\prime} \theta_1^{\prime}$ respectively , $\left(\theta_2>\theta_1\right)$. The temperature at the interface is

1) $\frac{\theta_1}{10}+\frac{9 \theta_2}{10}$
2) $\frac{\theta_2+\theta_1}{2}$
3) $\frac{\theta_1}{6}+\frac{5 \theta_2}{6}$
4) $\frac{\theta_1}{3}+\frac{2 \theta_2}{3}$

Solution:

Thermal Conductivity

$Q=\frac{K A\left(\theta_1-\theta_2\right) t}{l}$

K = thermal conductivity

Let the temperature of the interface be T

$\Rightarrow Conservation \:\:of \:\:heat$

$\begin{aligned} & \frac{T-\Theta_2}{d / 3 k A}+\frac{T-\Theta_1}{3 d / k A}=0 \\ & \Rightarrow 3 T-3 \theta_2+\frac{T}{3}-\frac{\theta_1}{3}=0 \\ & \Rightarrow 9 T-9 \theta_2+T-\theta_1=0 \\ & \Rightarrow T=\frac{9}{10} \theta_2+\frac{\theta_1}{10}\end{aligned}$

Hence, the answer is the option (2).

Example 3: A heat source at $T=10^3 K$ is connected to another heat reservoir at $T=10^2 K$ by a copper slab which is 1m thick. Given that the thermal conductivity of copper is 0.1 $W K^{-1} m^{-1}$ the energy flux (Wm^-2) through it in the steady state is:

1)90

2)120

3)65

4)200

Solution:

Thermal Conductivity

$Q=\frac{K A\left(\theta_1-\theta_2\right) t}{l}$

K = thermal conductivity

$\begin{aligned} & \left(\frac{d Q}{d t}\right)=\frac{k A \Delta T}{l} \\ & \text { energy flux }=\frac{1}{A}\left(\frac{d Q}{d t}\right)=\frac{k \Delta T}{l}=\frac{0.1 \times 900}{1}=90 \mathrm{~W} / \mathrm{m}^2\end{aligned}$

Hence, the answer is the option (1).

Example 4: The figure shows a system of two concentric spheres of radii $r_1$ and $r_2$ and kept at temperatures $T_1$ and $T_2$ respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

1) $\frac{r_1 r_2}{\left(r_2-r_1\right)}$
2) $\ln \left(r_2-r_1\right)$
3) $\frac{\left(r_2-r_1\right)}{r_1 r_2}$
4) $\ln \left(\frac{r_2}{r_1}\right)$

Solution:

Thermal Conductivity

$Q=\frac{K A\left(\theta_1-\theta_2\right) t}{l}$

K = thermal conductivity

wherein

Rate of flow of heat $\frac{d \theta}{d t}=\frac{K A \Delta T}{L}$

We have a spherical shell of radius r and thickness dx

$\begin{aligned} & A=4 \pi r^2, L=d r \\ & \frac{d \theta}{d t}=\frac{K 4 \pi r^2 d T}{d r} \\ & 4 \pi K \int_{T_1}^{T_2} d T=\frac{d \theta}{d t} \int_{r_1}^{r_2} \frac{d r}{r^2}=\frac{d \theta}{d t}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) \\ & 4 \pi K\left(T_2-T_1\right)=\frac{d \theta}{d t}\left(\frac{r_2-r_1}{r_2 r_1}\right) \\ & \therefore \frac{d \theta}{d t} \propto \frac{r_2 r_1}{r_2-r_1}\end{aligned}$

Hence, the answer is the option (3).

Example 5: Two points A and B are separated by a distance of 5cm respectively 15^o C and 35^o C respectively then the temperature gradient (in ^oC /m) will be

1) 400

2) 200

3) 600

4) 800

Solution:

Temperature Gradient

Rate of change of temperature with position between two isothermal surfaces.

wherein

Temprature gardient $=\frac{\Delta T}{\Delta x}=\frac{35^{\circ} \mathrm{C}-15^{\circ} \mathrm{C}}{5 \mathrm{~cm}}=400^{\circ} \mathrm{C} / \mathrm{m}$

Hence, the answer is the option (1).

Summary

Steady conduction heat transfer is a process where heat flows consistently through a material, maintaining a constant temperature difference. Key principles include the dependence of heat transfer on the medium, the increase in temperature in the direction of heat flow, and its occurrence in all states of matter. Understanding concepts like thermal conductivity, temperature gradients, and the behavior of heat in solids is essential for solving practical problems related to heat transfer.