The Maxwell Distribution Laws
Maxwell’s distribution laws describe particle speed or velocity frequency distribution in gas at any given temperature. The collection of rules was produced by James Clerk Maxwell in the 19th century and provides a consistent means through which one can predict what gas molecules do. They are proof although that the majority is within some middle ground speed-wise for particles but always a few either at high velocities or lower velocities which move too slow hence making them important in describing different gases` physical characteristics.
This Story also Contains
- What is Root mean square speed?
- What is the Most probable speed?
- What is Average speed?
- What is Maxwell’s Law?
- Solved Examples Based on The Maxwell Distribution Laws
- Summary
In this article, we will cover the concept of the Maxwell distribution Laws. This topic we study in the kinetic theory of gases, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), Twenty-six questions have been asked on this concept. And for NEET three questions was asked from this concept.
Let's read this entire article to gain an in-depth understanding of the Maxwell Distribution law, we have to discuss some basic terms related to it.
What is Root mean square speed?
It is defined as the square root of the mean of squares of the speed of different molecules.
ie. vms=v12+v22+v32+v42+…N=v¯2
As the Pressure due to an ideal gas is given as
P=13ρvrms2⇒vrms=3Pρ=3PV Mass of gas =3RTM=3kTm
Where,
R = Universal gas constant
M = molar mass
P = pressure due to gas
$\rho$ = density
- vrmsαT I.e With the rise in temperature, rms speed of gas molecules increases.
- vrmsα1M I.e With the increase in molecular weight, rms speed of the gas molecule decreases.
- The rms speed of gas molecules does not depend on the pressure of the gas (if the temperature remains constant)
What is the Most probable speed?
This is defined as the speed which is possessed by maximum the fraction of the total number of molecules of the gas.
I.e;vmps=2Pρ=2RTM=2kTm
What is Average speed?
It is the arithmetic mean of the speeds of molecules in a gas at a given temperature.
vavg=v1+v2+v3+v4+…N
And according to the kinetic theory of gases
vavg=8Pπρ=8πRTM=8πkTm
The relation between RMS speed, average speed, and most probable speed
Vrms>Vavg >Vmps
Recommended Topic Video
What is Maxwell’s Law?
The vrms (Root mean square velocity) gives us a general idea of molecular speeds in a gas at a given temperature. So, it doesn't mean that the speed of each molecule is vrms.
Many of the molecules have speeds less than vrms and many have speeds greater than vrms. So, Maxwell derived an equation that describes the distribution of molecules at different speeds as -
dN=4πN(m2πkT)3/2v2e−mv22kTdv
where, dN= Number of molecules with speeds between v and v+dv
So, from this formula, you have to remember a few key points
1. dNdv∝N
2. dNdv∝v2

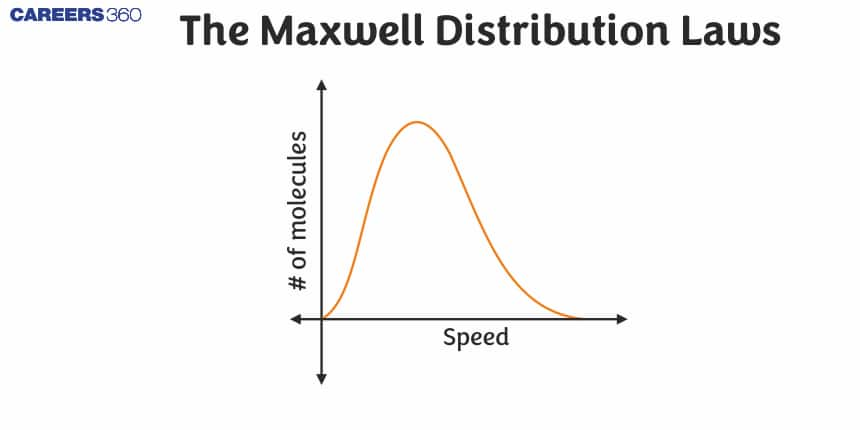
Conclusions From This Graph
1. This graph is between a number of molecules at a particular speed and the speed of these molecules.
2. You can observe that the dNdv is maximum at the most probable speed.
3. This graph also represent that vrms>vav>vmp.
4. This curve is the asymmetric curve.
5. From this curve we can calculate the number of molecules corresponding to that velocity range by calculating the area bonded by this curve with the speed axis.
Effect of temperature on velocity distribution
With the rising of temperature, the curve starts shifting right side and becomes broader as shown as -


Solved Examples Based on The Maxwell Distribution Laws
Example 1: The value closest to the thermal velocity of a Helium atom at room temperature (300 K)ms−1 is : [kB=1.4×10−23 J/K;mHe=7× 10−27 kg]
1) 13000
2) 1300
3) 130000
4) 130
Solution:
v=3kTm=3∗1.4∗10−23∗3007∗10−27v=1.8∗106=1.3∗103 m/s
Hence, the answer is option (2).
Example 2: At room temperature, a diatomic gas is found to have an r.m.s. speed of 1930 ms-1. The gas is :
1) H2
2) Cl2
3) O2
4) F2
Solution:
Root mean square velocity
Vrms=3RTM=3Pρ
At room temperature T = 300 K
For diatomic gas,
Vrms=3RTM=⇒M=3RTV2M=3×8.3×300(1930)2=2 g/mole
The diatomic gas is H2
Hence, the answer is the option (1).
Example 3: An ideal gas is enclosed in a cylinder at pressure of 2 atm and temperature 300 K. The mean time between two successive collisions is 6∗10−8 s. If the pressure is doubled and the temperature is increased to 500 K, the mean time (in sec) between two successive collisions will be close to:
1) 5×10−8 s
2) 2×10−8 s
3) 3×10−8 s
4) 4×10−8 s
Solution:
Root mean square velocity
Vrms=3RTM=3Pρ
wherein
R = Universal gas constant
M = molar mass
P = pressure due to gas
$\rho$ = density
Vrms∝TVrms∝ mean freepath timebetweensuccessivecollision
and mean free path =
Y=kT2πσ2P
Vrms∝YbVrms∝Tp×t…….1 but Vrms∝T……….2
From 1 and 2,
T∝TP×tt∝Tpt2t1=(T2T1)×(P1P2)=500300×P12P1=56t2=56t1t2≈4×10−8 s
Hence, the answer is option (4).
Example 4: A 15 g mass of nitrogen gas is enclosed in a vessel at a temperature 27∘C. The amount of heat (in kJ ) transferred to the gas, so that rms velocity of molecules is doubled is about: [ Take R = 8.3J/K mole ]
1) 10
2) 6
3) 14
4) 0.9
Solution:
Root mean square velocity
Vrms=3RTM=3Pρ
As gas is a closed vessel
Q=nCVΔTV∝T
RMS velocity is doubled
⇒>T2=4T1∴Q=nCV(4T1−T1)=nCV⋅3T1=1528×52R×3×300=10000 J=10 kJ
Hence, the answer is the option (1).
Example 5: A mixture of 2 moles of helium gas (atomic mass =4u ) and 1 mole of argon gas (atomic mass =40u ) is kept at 300 K in a container. The ratio of their ds [Vrms( helium )Vrms( argon )] is close to:
1) 3.16
2) 0.32
3) 0.45
4) 2.24
Solution:
Root mean square velocity -
Vrms=3RTMVrms(He)Vrms(Ar)=MArMHe=404=10
= 3.16
Hence, the answer is the option (1).
Summary
The Maxwell Distribution Laws provide a general description of the spread of gas-specific particle velocities and their effects on the pressure of a gas. This paper reports the existence of various molecular speeds with a greater number of particles that move at a mean speed while others have slow or very high velocities. This realization is important in understanding gas properties under various conditions such as pressure and heat.