Total Internal Reflection - Definition, Formula, Example, FAQs

What is Total Internal Reflection?

Total Internal Reflection is the phenomenon in which a light ray traveling from a denser medium to a rarer medium is completely reflected back into the denser medium, instead of refracting into the rarer medium.

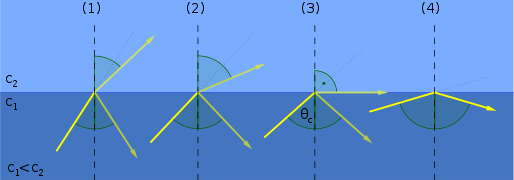
When Does Total Internal Reflection Occur?

Consider two lights passing through an optically denser media and into an optically rarer material at specific points.

The refraction of light is the phenomenon that causes light to bend off its normal path. This is a unique situation in which the refracted angle exceeds the incident angle.

The above statement describes how increasing the angle of incidence causes the angle of refraction to increase.

There is still a moment where the refraction angle becomes perpendicular. The refracted light will become parallel to the interface as a result of this.

The refracted ray angle of the rarer medium corresponds to the incident ray angle of the denser medium, which is 90°. This is called the critical angle of total internal reflection (c).

The ray returns to the same medium when it is incident on the surface at an angle larger than the critical angle. Total internal reflection refers to the full process of returning a light beam away from a denser medium. So total internal reflection occurs when the incidence angle is greater than the critical angle.

What are the Conditions of Total Internal Reflection?

There are two primary factors that influence whether or not the phenomena of total internal reflection occurs. (TIR) is founded on. A little difference in the two circumstances may not yield the desired effect.

There are two prerequisites for total internal reflection:

1. Light incident at the interface of two different media should prefer to pass from a denser to a rarer medium.
2. For these two media, a larger angle of incidence is required than the critical angle.

Total Internal Reflection Formula

Snell's Law: $n_1 \sin i=n_2 \sin r$
Critical Angle Formula: $\Theta_{\text {crit }}=\sin ^{-1}\left(\frac{n_2}{n_1}\right)$

Also Read:

• NCERT solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments
• NCERT notes Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Total Internal Reflection Examples

Here are some examples of total internal reflection:

Total internal reflection in optical fibre

One of the most important applications of total internal reflection is seen in optical fiber. In an optical fiber, the total internal reflection approach is used. The core of the higher refractive index fiber contains the inner component of the fiber. Another layer of glass surrounds all of these fibers. They have a refractive index that is just below that of the lower refractive index. The fibers are protected by a plastic jacket.

When light from one end of the core goes toward the cladding and propagates through it, this is known as back to back total internal reflection. Optical fibers have a lot of uses in the medical field, especially for endoscopy.

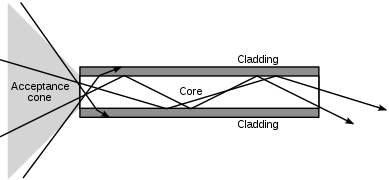
Define Acceptance angle:

The acceptance angle of an optical fiber is determined by ray optics is the maximum angle of a ray striking the fiber core (against the fiber axis) that allows incident light to be directed by the core. The numerical aperture is defined as the sine of that permissible angle (assuming an incident ray in air or vacuum) and is mostly governed by the refractive index contrast between the core and cladding of the fiber (assuming an incident ray in air or vacuum):

Acceptance angle formula

$\theta_{\text {acc }}=\frac{1}{n_0} \sqrt{n_{\text {core }}^2-n_{\text {cladding }}^2}$

n ₀ = refractive index of the medium around the fibre

n_core = refractive index of core

n_cladding = refractive index of cladding

θ_acc = acceptance angle

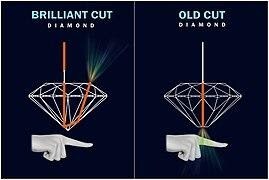
Diamond:

Total internal reflection in diamond: The incident ray is greater than the critical angle when it falls on every face of the diamond. The diamond's critical value is 23°. This situation is responsible for a diamond's entire internal reflection, which causes it to shine.

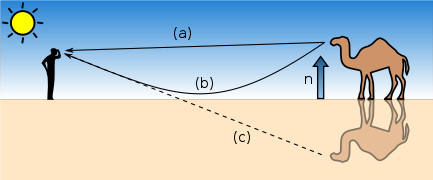
Mirage:

It's an optical illusion that causes the water layer to appear at short distances in the desert or on the road. Total internal reflection, which happens as a result of atmospheric refraction, is an example of a mirage.

Solved Examples on Total Internal Reflection

Q1. The refractive index of glass is $\sqrt{ } 2$. Find the critical angle for a glass-air interface.

Denser medium: Glass, $n_1=\sqrt{2}$
Rarer medium: Air, $n_2=1$

Using the formula:

$
\begin{gathered}
\sin c=\frac{n_2}{n_1}=\frac{1}{\sqrt{2}} \\
\sin c=\frac{1}{\sqrt{2}}=\sin 45^{\circ} \\
c=45^{\circ}
\end{gathered}
$
Answer: The critical angle is $\mathbf{4 5}^{\circ}$.

Q2. A light ray inside a glass block ( $n=\frac{2}{\sqrt{3}}$ ) strikes the glass-air surface at an angle of $30^{\circ}$. Will TIR occur?

The critical angle:

$
\begin{gathered}
\sin c=\frac{n_2}{n_1}=\frac{1}{\frac{2}{\sqrt{3}}}=\frac{\sqrt{3}}{2} \\
\sin c=\frac{\sqrt{3}}{2}=\sin 60^{\circ} \\
c=60^{\circ}
\end{gathered}
$

Angle of incidence $=30^{\circ}$
Critical angle $=60^{\circ}$
Since $30^{\circ}<60^{\circ}$, TIR will not occur.

Answer: No, TIR will not occur. The ray will refract into the air.

Q3. The critical angle for a certain material in air is $30^{\circ}$. Find its refractive index.
Solution:

$
\begin{aligned}
& \sin c=\frac{n_2}{n_1} \\
& \sin 30^{\circ}=\frac{1}{n_1} \\
& \frac{1}{2}=\frac{1}{n_1} \\
& n_1=2
\end{aligned}
$

Answer: The refractive index of the material is $\mathbf{2}$.

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects

Related Topics Link,

• Angle of Incidence
• Reflection of Light
• Refraction and Dispersion of Light through a Prism
• Refraction of Light
• Refractive Index