Travelling Waves

Travelling waves are a fundamental concept in physics, representing the transfer of energy through a medium without the permanent displacement of the medium itself. These waves, whether they are sound waves, light waves, or water waves, demonstrate how energy can move from one place to another, carrying information and facilitating various processes in nature. In real life, travelling waves are all around us—every time we speak, sound waves travel through the air to reach another person's ears; when we drop a stone in water, ripples spread outward as travelling waves. Even the light from the sun reaches us through electromagnetic waves, enabling life on Earth. In this article, we will discuss how travelling waves help us grasp how energy, signals, and even ideas move and interact within our world.

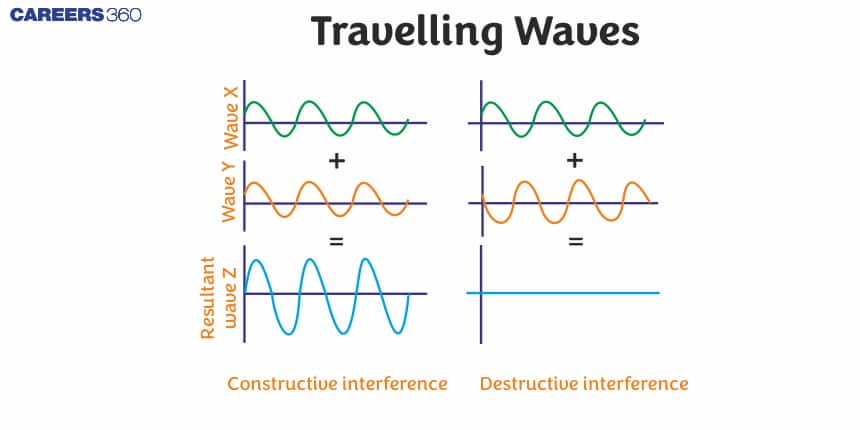
Travelling Waves

Travelling waves are a fascinating phenomenon in physics, representing the movement of energy through a medium in a continuous and systematic manner. Unlike standing waves, which remain fixed in space, travelling waves move, transporting energy from one location to another. This concept is crucial in understanding a wide range of natural and technological processes. In our daily lives, travelling waves are everywhere—when you throw a stone into a pond, the ripples that spread out are travelling waves. Similarly, the sound of a ringing bell reaches our ears through sound waves travelling through the air. Even light from the sun, which travels through the vacuum of space to reach Earth, is a form of travelling electromagnetic wave.

In mathematics, a periodic travelling wave, or wavetrain, is a periodic function of one-dimensional space that travels with constant speed. It is, therefore, a special case of a spatiotemporal oscillation which is a periodic function in space and time.

Travelling Waves Equation

The function $f(x,t)$ represents the displacements $y$ of the particle at $t=0$ and $x=x^{\prime }$
$y=f(x=x^{\prime },t=0)=A\sin \left(k{x}^{\prime }\right)$
k- propagation constant or angular wave number
A- Amplitude
For a given time, between position $x=0$ to $x=x^{\prime }$ the phase changes from 0 to $k{x}^{\prime }$ similarly, $x=0$ to $x=\lambda$ the phase changes from 0 to $2\pi$
$\begin{array}{rl}& x^{\prime }\to k{x}^{\prime }\\ & \lambda \to 2\pi \end{array}$
$k=\frac{2\pi }{\lambda }$
kx ' represents phase of wave at $\mathrm{x}={\mathrm{x}}^{\prime }$

The disturbance travels on the strings along the positive $x$-axis with a constant speed ' $v$ '. Thus, the displacement produced at the left end at time ' $t=0$ ', reaches the point ' $x$ ' at time ' $t=(x-x^{\prime })/v$ '.
As wave shape remains the same for progressive wave, particle's displacement at $\mathrm{x}={\mathrm{x}}^{\prime },\mathrm{t}=0$ and $\mathrm{x}={\mathrm{x}}^{\prime }+\mathrm{vt},\mathrm{t}=\mathrm{t}$ are the same
i.e., $y=f(x=x^{\prime },t=0)$ is the same as $y=f(x,t)$

Let's now write the equation in terms of the stationary coordinate x, where ${\underset{―}{x}}^{\prime }=\mathrm{x}-\mathrm{vt}$
$\begin{array}{c}y=f(x^{\prime },0)=f(x,t)\\ \therefore y(x,t)=A\sin \left(k{x}^{\prime }\right)=A\sin (k(x-vt))\end{array}$
$\begin{array}{rl}& y(x,t)=A\sin (k(x-vt))=A\sin (\frac{2\pi x}{\lambda }-\frac{2\pi vt}{\lambda })=A\sin (kx-\omega t)\\ & v=f\lambda =\frac{\lambda }{T}\\ & T=\frac{2\pi }{\omega }\end{array}$

$y(x,t)=A\sin (k(x-vt))=A\sin (\frac{2\pi x}{\lambda }-\frac{2\pi t}{T})=A\sin (kx-\omega t)$

For waves travelling along the negative $x$-axis,
$y(x,t)=A\sin (k(x+vt))=A\sin (\frac{2\pi x}{\lambda }+\frac{2\pi t}{T})=A\sin (kx+\omega t)$

GENERAL EQUATION OF TRAVELLING WAVE
$y(x,t)=A\sin (k(x\pm vt)+\varphi )=A\sin (\frac{2\pi x}{\lambda }\pm \frac{2\pi t}{T}+\varphi )=A\sin (kx\pm \omega t+\varphi )$

Recommended Topic Video

Solved Examples Based on Travelling Waves

Example 1: The intensity of sound from a radio at a distance of 2 metres from its speaker is $1\times {10}^{-2}\mu w/m^2$. The intensity at a distance of 10 metres would be

1) $0.2\times {10}^{-2}\mu w/{\mathrm{m}}^2$
2) $1\times {10}^{-2}\mu \mathrm{w}/{\mathrm{m}}^2$
3) $4\times {10}^{-4}\mu \mathrm{w}/{\mathrm{m}}^2$
4) $5\times {10}^{-2}\mu w/m^2$

Solution:

The intensity of the wave

Energy is transmitted per unit area per second in the form of a wave in the direction of the wave by source.

We know

$I\alpha \frac{1}{r^2}\Rightarrow \frac{I_2}{I_1}=\frac{r_1^2}{r_2^2}\Rightarrow \frac{I_2}{1\ast {10}^{-2}}=\frac{2^2}{{10}^2}=\frac{4}{100}\Rightarrow I_2=\frac{4\ast {10}^{-2}}{100}$

$=4\times {10}^{-4}\mu \mathrm{w}/{\mathrm{m}}^2$

Hence, the answer is the option (3).

Example 2: At t = 0, a transverse wave pulse travelling in +ve -direction, with the speed of 2 m/s by the function $y=\frac{6}{x^2},x\ne 0$. Transverse velocity of the particle at x = 2 m and t = 2s is

1) 3 m/s

2) -3 m/s

3) 8 m/s

4) -8 m/s

Solution:

Relation between phase velocity and wave speed

$V_P=-V\frac{dy}{dx}$

wherein

$\begin{array}{rl}& V_P=\text{particle velocity}\\ & V=\text{wave velocity}\\ & \frac{dy}{dx}=\text{slope of curve}\\ & \mathrm{y}[\mathrm{x},\mathrm{t}=0]=\frac{6}{x^2},\mathrm{y}[\mathrm{x},\mathrm{t}]=\frac{6}{(x-2t{)}^2}\\ & \frac{dy}{dt}=\frac{24}{(x-2t{)}^3}\text{at}\mathrm{x}=2,\mathrm{t}=2\\ & {\mathrm{v}}_{\mathrm{y}}=\frac{24}{(-2{)}^3}=-3\mathrm{m}/\mathrm{s}\end{array}$

Hence, the answer is the option (2).

Example 3: The wave function of two particles is given by $y_1=a\sin (\omega t-kx),y_2=a\sin (kx+\omega t)$, then

1) They are moving in the opposite direction
2) The phase difference between them is ${90}^{\circ }$
3) The phase difference between them is ${180}^{\circ }$
4) The phase difference between them is $0^{\circ }$

Solution:

General equation of travelling wave

For waves travelling along the positive x-axis,

$y(x,t)=A\sin (k(x-vt))=A\sin (\frac{2\pi x}{\lambda }-\frac{2\pi t}{T})=A\sin (kx-\omega t)$

For waves travelling along the negative x-axis, $y(x,t)=A\sin (k(x+vt))=A\sin (\frac{2\pi x}{\lambda }+\frac{2\pi t}{T})=A\sin (kx+\omega t)$

Both waves are moving opposite to each other.

Hence, the answer is the option (3).

Example 4: A wave travelling along the x-axis is described by the equation $y(x,t)=0.005\cos (\alpha x-\beta t)$. If the wavelength and the time period of the wave are 0.08 m and 2.0 s, respectively, then $\alpha$ and $\beta$ in appropriate units are

1) $\alpha =12.50\pi ,\beta =\frac{\pi }{2.0}$
2) $\alpha =25.00\pi ,\beta =\pi$
3) $\alpha =\frac{0.08}{\pi },\beta =\frac{2.0}{\pi }$
4) $\alpha =\frac{0.04}{\pi },\beta =\frac{1.0}{\pi }$

Solution:

Speed of sinusoidal wave

Wave Speed

$\frac{dx}{dt}=v=\frac{\omega }{k}$
wherein
$\begin{array}{rl}& \omega =2\pi \nu \\ & k=\frac{2\pi }{\lambda }\\ & y={10}^3\sin (50t+2x)\end{array}$

General $e{q}^n$
$y=a\sin (wt+kx)$

So, the wave is moving along the $x$-axis with speed $v$
$\mathrm{\&}=\frac{w}{k}=\frac{50}{2}=25\mathrm{m}/\sec$

Hence, the answer is the option (2).

Example 5: A progressive wave travelling along the positive x-direction is represented by $y(x,t)=A\sin (kx-wt+\varphi )$. Its snapshot at t=0 is given in the figure.

For this wave, the phase $\varphi$ is :

1) 0
2) $-\frac{\pi }{2}$
3) $\frac{\pi }{2}$
4) $\pi$

Solution:

Travelling Wave Equation

$y=A\sin (Kx-\omega t)$
wherein
$\begin{array}{rl}& K=2\pi /\lambda \\ & \omega =\frac{2\pi }{T}\end{array}$
$\lambda =$ wavelength
$T=$ The time period of oscillation
$y=A\sin (kx-wt+\varphi )$
at $x=0,t=0,y=0$
and the slope is negative
$\Rightarrow \varphi =\pi$

Hence, the answer is the option (4).

Summary

Travelling waves are essential in understanding the transfer of energy through a medium without permanent displacement. These waves, whether sound, light, or water, are key to many natural and technological processes. The wave equation describes their motion mathematically, helping us solve problems related to wave intensity, speed, and direction. In everyday life, travelling waves are everywhere, from the sound we hear to the light we see, demonstrating the widespread impact of this physical concept.