Triangle Law of Vector Addition

Triangle Law of Vector Addition - Examples, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 04:38 PM IST

The Triangle Law of Vector Addition is a fundamental concept in physics and mathematics that helps us understand how to add two vectors geometrically. According to this law, if two vectors are represented as the two sides of a triangle, taken in order, their resultant is represented by the third side of the triangle, taken in the reverse order. This principle is widely used in fields like mechanics, navigation, and electromagnetism to analyze forces, velocities, and other vector quantities. In this article, we’ll break down the law, its derivation, and practical applications.

This Story also Contains

Introduction to Vector Addition
Triangle Law of Vector Addition
Derivation of the Triangle Law of Vector Addition
Parallelogram Law of Vector Addition
Triangle Law of Forces
How to Find the Direction of the Resultant Vector?
Example of Triangle Law of Vector Addition
Important Points About Vector Addition
Summary

Triangle Law of Vector Addition - Examples, FAQs

Introduction to Vector Addition

Vector Addition is the process of combining two or more vectors to determine a resultant vector, which represents the overall effect of those vectors. Vectors are quantities that have both magnitude and direction, such as force, velocity, or displacement. Unlike scalar quantities, which can be simply added arithmetically, vectors require both magnitude and direction to be considered in their addition.

There are two primary methods of vector addition: the Triangle Law and the Parallelogram Law. In both cases, the individual vectors are placed tail to head, and the resultant vector is drawn from the starting point to the endpoint.

Laws of Vector Addition

Vectors are written/represented with an alphabet and an arrow over them and are represented as a combination of direction and magnitude. The addition of two or more vectors is referred to as vector addition. When we add vectors, we use the addition operation to add two or more vectors to obtain a new vector that equals the sum of the two or more vectors. The addition of vector can be used to combine two vectors, a and b, and thus the resultant vector can be expressed as:

R = a+ b here bold is used to show that R, a and b are vectors

There are different laws of vector addition and these are:

Triangle Law of Vector Addition

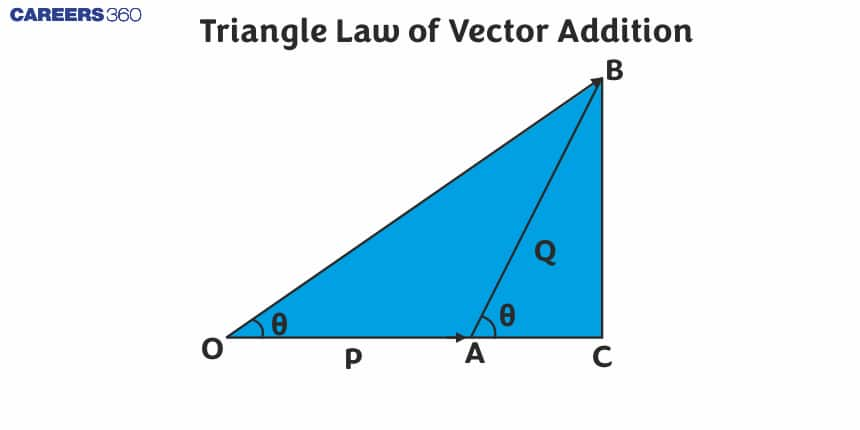
The triangle law of vector addition states that if two vectors are represented by the sides of a triangle taken in order of magnitude and direction, then the resultant sum of the vectors is given by the triangle's third side in reverse order of magnitude and direction.

Mathematically, if you have two vectors A and B, and you place the tail of vector B at the head of vector A, then the resultant vector R is the vector drawn from the tail of A to the head of B. The direction and magnitude of this resultant vector represent the combined effect of both vectors.

Derivation of the Triangle Law of Vector Addition

Consider two vectors P and Q, represented in both magnitude and direction by the sides OA and AB of a triangle OAB, respectively. Let R be the product/resultant of the triangle law of vector additions. The resultant of P and Q is therefore represented by side OB according to the triangle law of addition or triangle law of vector addition.

Tringle law of vector addition

We have,

$$
R=P+Q
$$

Expand A to C and draw perpendicular BC .
From triangle OCB we have,

$$
\begin{aligned}
& \mathrm{OB}^2=\mathrm{OC}^2+\mathrm{BC}^2 \\
& \mathrm{OB}^2=(\mathrm{OA}+\mathrm{OC})^2+\mathrm{BC}^2
\end{aligned}
$$

In the triangle ACB,

$$
\begin{aligned}
& \cos \theta=A C / A B \\
& A C=A B \cos \theta=Q \cos \theta
\end{aligned}
$$

Also,

$$
\sin \theta=B C / A B
$$

$$
B C=A B \sin \theta=Q \sin \theta
$$

Resultant magnitude:
Substitute the values for $A C$ and $B C$ in (i),

$$
\begin{aligned}
& R^2=(P+Q \cos \theta)^2+(Q \sin \theta)^2 \\
& R^2=P^2+2 P Q \cos \theta+Q^2 \\
& R=\sqrt{ }\left(P^2+2 P Q \cos \theta+Q^2\right)
\end{aligned}
$$
The above equation gives us the magnitude of the resultant.

Parallelogram Law of Vector Addition

The Parallelogram Law of Vector Addition is another fundamental method for determining the resultant of two vectors. This law states that if two vectors are represented as adjacent sides of a parallelogram, then the diagonal of the parallelogram that starts from the common point of the vectors represents their resultant.

Here's how it works:

Draw the Vectors: Start by placing the vectors A and B such that they both originate from the same point.
Form a Parallelogram: Complete the parallelogram by drawing lines parallel to A and B from the endpoints of each vector.
Draw the Resultant: The diagonal of the parallelogram that extends from the common point of the vectors to the opposite corner represents the resultant vector R.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Prallelogram law of vector addition

Triangle Law of Forces

The Triangle Law of forces is applicable when there are three forces acting on a body in equilibrium. The two forces are then represented as two sides of a triangle in the same order, with their magnitude scaled to a suitable scale, and the resultant in the opposite order is the third side or closing side of the triangle.

The Triangle Law of Forces can also be used to calculate the resultant of two forces acting at a point.

Related Topic,

Mathematical Tools

Scalars And Vectors

Multiplication Of Vectors

Vector Addition And Vector Subtraction

How to Find the Direction of the Resultant Vector?

The direction of the magnitude of the resultant vector is given by;

From triangle OBC,
$tan⁡∅=BC/OC$
Since, $OC=OA+AC$ .
$tan⁡∅=BC/(OA+AC)$
$tan⁡∅=Qsin⁡θ/(P+Qcos⁡θ)$

The above equation gives us the direction of the resultant vector.

Example of Triangle Law of Vector Addition

Example: Two vectors A and B of magnitude 5 units and 7 units respectively make an angle of 60^o. Determine the magnitude of the resultant vector.

Solution: By following the triangle law of vector addition, the resultant vector is given by:
$R=A+B$
The magnitude of $R$ is:

$R=|R|=72+52+2∗5∗7cos⁡60∘R=25+49+70/2R=109 units$

Important Points About Vector Addition

Here is a list of some points to keep in mind while studying vector addition:

Vectors are depicted with an arrow and are represented as a combination of direction and magnitude.
If we know the components of a vector, we can calculate the direction of the resultant vector.
The well-known triangle law of forces can be used to add vectors, and this method is also known as the head-to-tail method.

Also, check-

NCERT Physics Notes:

Summary

The sum of two vectors can be found mathematically using the triangular law of vector addition. Mathematical physics includes vector addition and subtraction as essential concepts. A vector is an entity with both magnitude and direction, sometimes known as a quantity. It is a geometric addition of the vectors.

Frequently Asked Questions (FAQs)

1. Explain the triangle law of the vector addition method.

The Triangle Law of Vector Addition states that when two vectors are represented by two sides of a triangle in order of magnitude and direction, the magnitude and direction of the resultant vector are represented by the third side of the triangle.

2. What Are the Vector Addition Properties?

Vector addition meets two important properties

1. In commutative law, the order of addition is irrelevant, so A+B is equal to B+A.

2. The Associative law states that the sum of three vectors is independent of which pair of vectors is added first, i.e. (A+B)+C=A+(B+C).

3. What is the parallelogram law of vector addition?

According to the Parallelogram law of vector addition, if any two vectors a and b represent two sides of a parallelogram in magnitude and direction, then their sum a + b equals the diagonal of the parallelogram across their common point in magnitude and direction.

4. What is vector addition's commutative property and associative property?

The commutative property of vector addition asserts that for any two vectors a and b,

a + b = b + a.

According to the Associative Property of Vector addition, for any three vectors a, b, and c,

(a + b ) + c = a + (b + c )

5. What does the magnitude of a vector mean?

The magnitude of a vector denotes the length of the vector. The magnitude of the vector a is denoted as |a|.

6. What is the polygon law of vector Addition?

Polygon law of vector addition states that if the number of vectors can be represented in magnitude as well as direction by side of a polygon taken in the same order, then their resultant is represented in magnitude along with direction by the closing side of the polygon taken in the opposite order

7. How do you calculate the magnitude of the resultant vector using the Triangle Law?

The magnitude of the resultant vector can be calculated using the formula R= P2+Q2+2PQcos⁡θ, where P and Q are the magnitudes of the two vectors, and θ is the angle between them.

8. How do you calculate the magnitude of the resultant vector using the Triangle Law?

The magnitude of the resultant vector can be calculated using the formula R= P2+Q2+2PQcos⁡θ, where P and Q are the magnitudes of the two vectors, and θ is the angle between them.

9. What is the purpose of the Triangle Law in physics?

The Triangle Law helps in understanding and calculating the combined effect of multiple vectors, such as forces or velocities, by visually representing and computing their resultant. It simplifies complex vector problems by breaking them into manageable components.

10. What role does the tail-to-tip method play in the Triangle Law?

The tail-to-tip method is fundamental to the Triangle Law. It involves placing the tail of the second vector at the tip of the first vector. The resultant vector is then drawn from the tail of the first vector to the tip of the second, forming a triangle.

11. What is the significance of the closed triangle in vector addition?

A closed triangle in vector addition signifies that the vectors form a complete loop. This is important because it visually represents the principle that the sum of the two original vectors plus the negative of the resultant vector equals zero, which is a fundamental concept in vector equilibrium.

12. How does the Triangle Law demonstrate the principle of vector resolution?

The Triangle Law inherently demonstrates vector resolution by showing how a single vector (the resultant) can represent the combined effect of two other vectors. Conversely, it shows how a vector can be resolved into two component vectors.

13. What is the relationship between the Triangle Law and the concept of vector projection?

Vector projection is closely related to the Triangle Law. When you project one vector onto another, you're essentially using a right-angled triangle. The projected vector becomes one side of this triangle, demonstrating how the Triangle Law underlies many vector operations.

14. What is the significance of the angle between vectors in the Triangle Law?

The angle between vectors in the Triangle Law is crucial as it determines both the magnitude and direction of the resultant vector. As the angle between vectors increases from 0° to 180°, the magnitude of the resultant generally decreases, illustrating how direction impacts vector addition.

15. What happens if the two vectors in the Triangle Law are perpendicular to each other?

When the two vectors are perpendicular, they form a right-angled triangle. In this case, the magnitude of the resultant vector can be calculated using the Pythagorean theorem: R² = A² + B², where R is the resultant and A and B are the magnitudes of the original vectors.

16. How does the angle between the two vectors affect the resultant in the Triangle Law?

The angle between the vectors influences both the magnitude and direction of the resultant. As the angle increases from 0° to 180°, the magnitude of the resultant generally decreases. At 0°, the resultant is maximum (sum of magnitudes), and at 180°, it's minimum (difference of magnitudes).

17. How does scaling a vector affect the Triangle Law of Vector Addition?

Scaling a vector changes its magnitude but not its direction. In the Triangle Law, if you scale one or both vectors, the shape of the triangle will change, affecting the magnitude and possibly the direction of the resultant vector.

18. How does the Triangle Law help in understanding vector components?

The Triangle Law illustrates how a vector can be broken down into components. By drawing a right-angled triangle with the vector as the hypotenuse, you can visualize and calculate its horizontal and vertical components, which is crucial in many physics applications.

19. How does the Triangle Law help in understanding the concept of relative velocity?

The Triangle Law is useful in relative velocity problems where you need to add or subtract velocity vectors. For instance, when calculating the velocity of an object relative to a moving reference frame, you can use the Triangle Law to combine the object's velocity with the negative of the reference frame's velocity.

20. Why is the direction of the resultant vector important in the Triangle Law?

The direction of the resultant vector is crucial because it represents the overall effect of the two original vectors. In the Triangle Law, the resultant vector points from the tail of the first vector to the tip of the second vector, indicating the net direction of the combined forces or displacements.

21. How can you determine the angle of the resultant vector using the Triangle Law?

The angle of the resultant vector can be determined geometrically by measuring the angle it makes with one of the original vectors. Alternatively, trigonometric functions can be used if the magnitudes of all sides and angles of the triangle are known.

22. Why is it important to maintain vector directions when applying the Triangle Law?

Maintaining correct vector directions is crucial because vectors are defined by both magnitude and direction. Incorrect directions will lead to an inaccurate resultant vector, misrepresenting the combined effect of the original vectors.

23. What is the importance of scale in drawing vector diagrams for the Triangle Law?

Scale is crucial in vector diagrams for the Triangle Law because it ensures that the relative magnitudes of the vectors are accurately represented. A consistent scale allows for proper visual comparison and measurement of vector magnitudes, leading to accurate results when solving problems graphically.

24. How does the Triangle Law help in understanding the concept of resultant displacement?

The Triangle Law is particularly useful in calculating resultant displacement. When an object undergoes multiple displacements, each can be represented as a vector. By applying the Triangle Law successively, you can determine the final position of the object relative to its starting point.

25. Can the Triangle Law be applied to more than two vectors?

The Triangle Law is primarily used for adding two vectors. For more than two vectors, you would need to apply the law multiple times in succession or use other methods like the Polygon Law of Vector Addition.

26. How does the magnitude of the resultant vector relate to the original vectors in the Triangle Law?

The magnitude of the resultant vector depends on both the magnitudes and directions of the original vectors. It is generally not equal to the sum of the magnitudes of the original vectors, except when the vectors are parallel and in the same direction.

27. Can the Triangle Law be used for subtracting vectors?

Yes, the Triangle Law can be used for vector subtraction. To subtract vector B from vector A, you add the negative of B to A. Graphically, this means reversing the direction of vector B before applying the Triangle Law.

28. What is the significance of the order of vector addition in the Triangle Law?

The order of vector addition doesn't affect the final result in the Triangle Law. Whether you draw vector A followed by vector B, or vector B followed by vector A, the resultant vector will be the same. This demonstrates the commutative property of vector addition.

29. How does the Triangle Law relate to real-world physics problems?

The Triangle Law is useful in various physics scenarios, such as calculating resultant forces, determining net displacement in motion problems, or analyzing velocity components in projectile motion. It provides a visual and intuitive way to understand vector combinations in physical systems.

30. What role does the Triangle Law play in understanding vector calculus concepts?

While the Triangle Law is a basic concept, it forms the foundation for understanding more complex ideas in vector calculus. For instance, it helps in visualizing how small changes in position (represented as vectors) can accumulate along a path, which is crucial for understanding line integrals.

31. Can the Triangle Law be used to add vectors of different units?

No, the Triangle Law can only be applied to vectors with the same units. Vectors represent physical quantities, and it's not meaningful to add vectors of different physical dimensions (e.g., velocity and force). All vectors in the addition must represent the same type of quantity.

32. What is the relationship between the Triangle Law and the concept of vector space?

The Triangle Law embodies fundamental properties of vector spaces, particularly the closure under addition. It visually demonstrates how the sum of two vectors in a vector space is another vector in the same space, which is a key property of vector spaces in linear algebra.

33. How does the Triangle Law relate to the concept of vector fields in electromagnetism?

In electromagnetism, the Triangle Law forms the basis for understanding how electric and magnetic field vectors can be added at each point in space. This is crucial for calculating resultant fields from multiple sources and for understanding concepts like superposition of fields.

34. How does the Triangle Law differ from the Parallelogram Law of Vector Addition?

While both laws are used for vector addition, the Triangle Law uses three sides of a triangle, where the third side represents the resultant vector. The Parallelogram Law, on the other hand, forms a parallelogram with the two vectors as adjacent sides, and the diagonal represents the resultant vector.

35. What is the relationship between the Triangle Law and the Parallelogram Law of Vector Addition?

The Triangle Law and the Parallelogram Law are essentially equivalent methods for vector addition. The triangle formed in the Triangle Law is half of the parallelogram formed in the Parallelogram Law. Both methods yield the same resultant vector, but the Triangle Law often requires less drawing.

36. How does the concept of vector subtraction relate to the Triangle Law?

Vector subtraction using the Triangle Law is essentially vector addition with a negative vector. To subtract vector B from vector A, you add the negative of B to A. Graphically, this means reversing the direction of vector B and then applying the Triangle Law as usual.

37. Can the Triangle Law be applied to quantum mechanical vectors?

While the Triangle Law is typically used for classical vectors, its principles can be extended to quantum mechanical state vectors in Hilbert space. However, the visualization becomes more abstract, and other mathematical tools are often more practical for quantum calculations.

38. How does the Triangle Law demonstrate the non-associative property of vector cross products?

While the Triangle Law itself deals with vector addition (which is associative), it can be used to visualize why vector cross products are non-associative. By attempting to apply the Triangle Law to cross products, one can see that the order of operations matters, unlike in vector addition.

39. How does the Triangle Law help in understanding force equilibrium in physics?

The Triangle Law is useful in analyzing force equilibrium. When multiple forces act on an object at rest, they must sum to zero. By using the Triangle Law repeatedly, you can visually represent how multiple forces combine to create equilibrium, with the final side of the polygon closing back to the starting point.

40. How does the concept of vector equilibrium relate to the Triangle Law?

Vector equilibrium occurs when the sum of all vectors equals zero. In the context of the Triangle Law, this would mean that the third side of the triangle (the resultant) has zero magnitude, effectively closing the triangle back to its starting point.

41. What role does the Triangle Law play in understanding vector fields?

While the Triangle Law itself doesn't directly apply to vector fields, it forms the basis for understanding how vectors can be added or subtracted at each point in a field. This is crucial for concepts like gradient, curl, and divergence in more advanced physics.

42. Can the Triangle Law be used to understand vector dot products?

While the Triangle Law is primarily used for vector addition, it can help visualize concepts related to dot products. For instance, the cosine of the angle between two vectors (used in dot product calculations) can be related to the sides of the triangle formed by these vectors.

43. How does the Triangle Law relate to the concept of vector decomposition in physics?

Vector decomposition is essentially the reverse process of the Triangle Law. While the Triangle Law combines two vectors to form a resultant, decomposition breaks a vector into components. This process is crucial in many physics applications, such as analyzing forces on an inclined plane.

44. What is the Triangle Law of Vector Addition?

The Triangle Law of Vector Addition is a graphical method for adding two vectors. It states that if two vectors are represented by two sides of a triangle taken in order, then the third side of the triangle represents their sum (resultant vector), but in the opposite direction.

45. What are the limitations of the Triangle Law of Vector Addition?

The main limitation is that it's most practical for adding only two vectors. For multiple vectors, it becomes cumbersome and prone to errors. Additionally, for very large or very small vectors, graphical representation might not be accurate enough for precise calculations.

46. Can the Triangle Law be used for three-dimensional vectors?

While the Triangle Law is typically used for two-dimensional vectors, it can be extended to three dimensions. However, this requires more complex spatial visualization and is often less practical than other methods for 3D vector addition.

47. Can the Triangle Law be used to find the difference between two vectors?

Yes, the Triangle Law can be used to find the difference between two vectors. To do this, you would add the negative of the second vector to the first vector. Graphically, this means reversing the direction of the second vector before applying the Triangle Law.

48. How does the Triangle Law relate to the concept of vector resolution in projectile motion?

In projectile motion, the Triangle Law helps in resolving the initial velocity vector into its horizontal and vertical components. This resolution forms a right-angled triangle, where the initial velocity is the hypotenuse, and the horizontal and vertical components form the other two sides.

49. How can the Triangle Law be used to explain the concept of relative motion?

The Triangle Law is useful in relative motion problems. For example, when calculating the velocity of an object relative to a moving observer, you can use the Triangle Law to add the object's velocity vector to the negative of the observer's velocity vector.

50. How does the Triangle Law help in understanding the concept of net force?

The Triangle Law is particularly useful in calculating net force when multiple forces act on an object. Each force can be represented as a vector, and by applying the Triangle Law successively, you can determine the magnitude and direction of the net force acting on the object.

51. How does the Triangle Law relate to the concept of vector resolution in circular motion?

In circular motion, the Triangle Law can help resolve velocity and acceleration vectors into radial and tangential components. This resolution forms right-angled triangles, where the total velocity or acceleration vector is the hypotenuse, and the radial and tangential components form the other two sides.

52. How can the Triangle Law be used to understand the concept of momentum conservation?

The Triangle Law can visualize momentum conservation in collisions. The total momentum before and after a collision can be represented as vectors. By applying the Triangle Law, you can see how the individual momenta of colliding objects combine to equal the total momentum, which remains constant.

53. How does the Triangle Law help in explaining the concept of work done by a force?

The Triangle Law can help visualize work done by a force, especially when the force is not parallel to the displacement. By forming a triangle with the force vector, displacement vector, and their resultant, you can see how only the component of force parallel to displacement contributes to work.

54. Can the Triangle Law be used to understand the concept of torque?

While torque is a cross product and not a simple vector addition, the Triangle Law can help visualize the components involved. It can show how the perpendicular component of a force contributes to torque, by resolving the force vector into parallel and perpendicular components relative to the lever arm.

55. What is the significance of the Triangle Law in understanding wave interference?

The Triangle Law can be applied to wave interference by representing wave amplitudes as vectors. The resultant amplitude of interfering waves can be found by applying the Triangle Law to these amplitude vectors, helping to visualize constructive and destructive interference.

56. How can the Triangle Law be used to explain the concept of center of mass?

While not directly related, the Triangle Law can help visualize how the center of mass is determined. By representing the positions of different masses as vectors and applying the Triangle Law with appropriate scaling, you can see how the center of mass is a weighted average of positions.

57. What role does the Triangle Law play in understanding the concept of mechanical advantage in simple machines?

The Triangle Law can help visualize force transformations in simple machines. For instance, in a lever, it can show how input and output forces relate, forming a triangle with the lever arm. This helps in understanding how mechanical advantage is achieved through vector relationships.

58. How does the Triangle Law contribute to understanding the concept of impulse in physics?

The Triangle Law can be used to visualize impulse, which is the change in momentum. By representing initial and final momentum as vectors, the impulse can be seen as the vector that completes the triangle between these two momentum vectors, illustrating both magnitude and direction of the change.

59. Can the Triangle Law be applied to understand the concept of phase in wave mechanics?

While not directly applicable, the Triangle Law can help visualize phase relationships in waves. By representing wave amplitudes at different phases as vectors, the Triangle Law can show how these combine, which is useful in understanding concepts like phasor addition in alternating current circuits.