Dalton's Law of Partial Pressure

Dalton's Law of Partial Pressures, is discoverd by chemist John Dalton. The law states that the total pressure exerted by a mixture of non-reacting gases is the sum of partial pressures exerted by each individual gas in the mixture. Partial pressure refers to the pressure that a gas would have if it took up the entire volume of the mixture all by itself. This law is an approximation of how all mixtures of gases behave under most industrial and natural conditions.

This Story also Contains

1. Dalton's law
2. Some Solved Examples
3. Summary

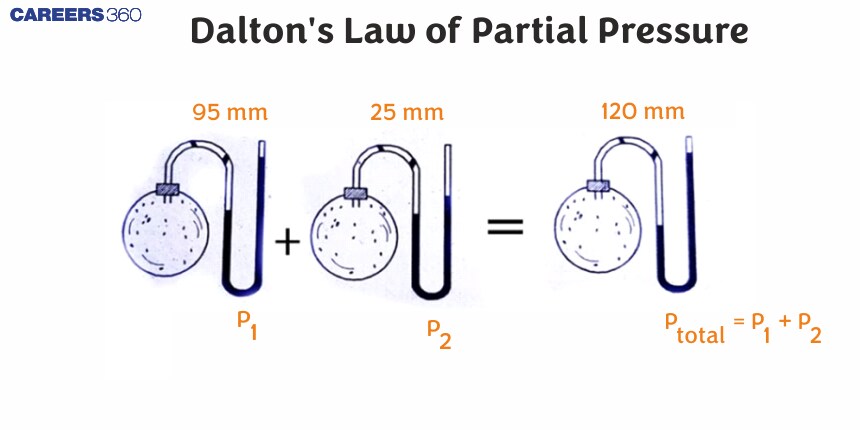
Dalton's law

The total pressure of a mixture of non-reacting gases is equal to the sum of partial pressure of these gases at constant temperature and constant volume."

$\begin{aligned} & P_{\operatorname{mix}}=P_1+P_2+P_3 \\ & \text { Here } P_{\operatorname{mix}}=\text { pressure of the gaseous mixture } \\ & P_1, P_2, P_3=\text { partial pressure of gases } \\ & \text { Partial pressure of any gas }=\frac{\% \text { of that gas }}{100} \times P_{\operatorname{mix}} \\ & \% \text { of a gas in a mixture }=\frac{\text { Partial pressure of the gas }}{\text { Total pressure of gaseous mixture }} \times 100\end{aligned}$

Partial pressure of any component $A$ is given as
$$
\mathrm{P}_{\mathrm{A}}=\frac{\text { moles of } \mathrm{A}}{\text { Total moles }} \times \mathrm{P}_{\text {Total }}
$$

Total pressure of a mixture having different components is given as
$$
\begin{aligned}
& \mathrm{P}_{\text {mix }}=\left(\mathrm{n}_1+\mathrm{n}_2+\mathrm{n}_3 \ldots \ldots\right) \frac{\mathrm{RT}}{\mathrm{V}} \\
& \mathrm{P}_{\text {mix }}=\left(\frac{\mathrm{w}_1}{\mathrm{~m}_1}+\frac{\mathrm{w}_2}{\mathrm{~m}_2}+\frac{\mathrm{w}_3}{\mathrm{~m}_3}\right) \ldots \frac{\mathrm{RT}}{\mathrm{V}}
\end{aligned}
$$

Here $\mathrm{w}_1, \mathrm{w}_2, \mathrm{w}_3=$ weight of components or non - reacting gases and $\mathrm{m}_1, \mathrm{~m}_2, \mathrm{~m}_3$ are their molar masses.

$\begin{aligned} & \mathrm{T}=\text { Temperature in Kelvin. } \\ & \mathrm{V}=\text { Volume in litre. }\end{aligned}$

• When a gas is collected over water it mixes with water vapors so the correct pressure of moist gas is given as
  P(moist gas) = P(dry gas) + P(VP of water)
  P(dry gas) = P(moist gas) - P(V.P of water)
  Aqueous tension = Partial pressure of water vapor in moist gas.
• Vapour pressure of the water varies with temperature. For example, Aa 0^oC, it is 4.6 torr while at 25^oC it is 23.8 torr.

NOTE: Dalton's law is not applicable for a mixture of reacting gases like N₂ and O₂, SO₂ and O₂.

Partial pressure in terms of mole fraction

According to ideal gas equation, if n₁ is the number of molecules of one constituent gas of the gaseous mixture then P₁ is the pressure exerted by the gas at temperature(T) enclosed in the volume (V).

$P_1=\frac{n_1 R T}{V}$
Similarly for the other two constituting gases of the gaseous mixture

$\begin{aligned} & P_2=\frac{n_2 R T}{V} \\ & P_3=\frac{\mathrm{n}_3 R T}{V}\end{aligned}$

According to Dalton's Law of partial pressures

$\begin{aligned} & P_{\text {Total }}=P_1+P_2+P_3+\ldots \\ & =\frac{n_1 R T}{V}+\frac{n_2 R T}{V}+\frac{n_3 R T}{V}+\ldots \\ & P_{\text {total }}=\left(n_1+n_2+n_3\right) \frac{R T}{V}\end{aligned}$

That means the total partial pressure of the mixture is determined by the total number of moles present.
Dividing equation (i) by (ii) we get.

$
\begin{aligned}
& \frac{\mathrm{P}_1}{\mathrm{P}_{\text {total }}}=\left(\frac{\mathrm{n}_1}{\mathrm{n}_1+\mathrm{n}_2+\mathrm{n}_3}\right) \frac{\mathrm{RTV}}{\mathrm{RTV}} \\
& =\frac{\mathrm{n}_1}{\mathrm{n}_1+\mathrm{n}_2+\mathrm{n}_3}=\frac{\mathrm{n}_1}{\mathrm{n}}
\end{aligned}
$
wheren $=\mathrm{n}_1+\mathrm{n}_2+\mathrm{n}_3$
Now, $\frac{\mathrm{n}_1\left(\text { moles of } 1^{\text {st }} \mathrm{gas}\right)}{\mathrm{n} \text { (Total number of moles })}=$ Mole fraction of first gas $\mathrm{x}_1$

Mole fraction:

It is the ratio of the number of moles of an individual gas to the total number of moles of all gases present in the container.

$
\frac{\mathrm{P}_1}{\mathrm{P}_{\text {total }}}=\mathrm{x}_1
$

Thus, $\mathrm{P}_1=\mathrm{x}_1 \mathrm{P}_{\text {total }}$
$
\text { Similarly } P_2=\mathrm{x}_2 \mathrm{P}_{\text {total }}
$

Therefore the generalised equation becomes
$
P_i=x_i P_{\text {Total }}
$

Where, P_i = partial pressure of the i^th gas
x_i = mole fraction of the i^th gas
Thus, the partial pressure of a gas in the mixture of gases is the product of its mole fraction and the total pressure of the mixture.

Applications

• Jet airplanes flying at high altitudes need pressurization of cabins so as to make partial pressure of oxygen sufficient for breathing, as the air pressure decreases with an increase in altitude.
• Calculation of the pressure of dry gas collected over water: When the gas is collected over water it is moist because of the water vapours. Saturated water vapour exerts its own partial pressure called aqueous tension. So, in order to calculate the partial pressure of dry gas, aqueous tension is subtracted from the pressure of moist gas (P_{moist gas} or P_Total)
  P_{dry gas} = P_total - Aqueous tension

Recommended topic video on (Dalton's Law of Partial Pressure)

Some Solved Examples

Example 1: Two gases of A and B having molar masses 60g and 45g respectively are enclosed in a vessel. The mass of A is 0.50g and that of B is 0.20g. The total pressure of the mixture is 750mm. Calculate the partial pressure of A and B gases respectively.

1)345.8mm, 260.7mm

2)589.2mm, 342.7mm

3)236.5mm, 432.5mm

4) 487.5mm, 262.5mm

Solution

We have:
Molar mass of A = 60g and molar mass of B = 45g
Given mass of A = 0.50g and given mass of B = 0.20g
Now, the total pressure of the mixture

$P_{\text {mixture }}$ = 750mm

Now, moles of A = 0.50/60 = 0.0084 moles
And, moles of B = 0.20/45 = 0.0045 moles
Again, mole fraction of A = 0.0084/0.0129 = 0.65
And, mole fraction of B = 0.0045/0.0129 = 0.35
Thus, partial pressure of A ($P_A$ ) = 750 x 0.65 = 487.5mm
Again, partial pressure of B($P_B$ ) = 262.5mm
Hence, the answer is the option (4).

Example 2: A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5 g neon. If the pressure of the mixture of gases in the cylinder is 25 bar. What is the partial pressure of dioxygen and neon in the mixture?

1) 5.25 bar, 19.75 bar

2)4.75 bar, 23.45 bar

3)6.20 bar, 20.44 bar

4)5.50 bar, 21.75 bar

Solution

Number of moles of $\mathrm{O}_2$ = 70.6g / 32g = 2.21 moles
And number of moles of $\mathrm{Ne}_2$ = 167.5 g / 20g = 8.375 moles
Now, mole fraction of $\mathrm{O}_2$ = 2.21 / (2.21+8.375)
= 0.21
And mole fraction of $\mathrm{Ne}_2$ = 8.375 / (2.21+8.375)
= 0.79
Now, according to Dalton’s law of partial pressure, we have:
Partial pressure = Mole fraction x Total pressure
Thus, partial pressure of $\mathrm{O}_2$ = 0.21 x 25 bar
= 5.25 bar
And, partial pressure of $\mathrm{Ne}_2$ = 0.79 x 25 bar
= 19.75 bar
Hence, the answer is the option (1).

Example 3: Dalton's law is not applicable for:

1) NH₃ and HCl

2)He and H₂

3)Ne and CO₂

4)Ar and Xe

Solution

Dalton's law applies to a mixture of non-reacting gases.

Since NH₃ and HCl combine to form NH₄Cl, hence Dalton's law will not be applicable.

$\mathrm{NH}_3+\mathrm{HCl} \longrightarrow \mathrm{NH}_4 \mathrm{Cl}$

Hence, the answer is the option (1).

Example 4: A mixture of one mole each of H₂, He, and O₂ each are enclosed in a cylinder of volume V at temperature T. If the partial pressure of H₂ is 2 atm,the total pressure of the gases in the cylinder is :

1) 6 atm

2)38 atm

3)14 atm

4)22 atm

Solution

According to Dalton's law of partial pressure

$\mathrm{p}_{\mathrm{i}}=\mathrm{x}_{\mathrm{i}} \times \mathrm{P}_{\mathrm{T}}$

Where

$\begin{aligned} & \mathrm{p}_{\mathrm{i}}=\text { partial pressure of the } \mathrm{i}^{\text {th }} \text { component } \\ & \mathrm{x}_{\mathrm{i}}=\text { mole fraction of the } \mathrm{i}^{\text {th }} \text { component } \\ & \mathrm{p}_{\mathrm{T}}=\text { total pressure of mixture } \\ & \Rightarrow 2 \mathrm{~atm}=\left(\frac{\mathrm{n}_{\mathrm{H}_2}}{\mathrm{n}_{\mathrm{H}_2}+\mathrm{n}_{\mathrm{He}}+\mathrm{n}_{\mathrm{O}_2}}\right) \times \mathrm{pT} \\ & \Rightarrow \mathrm{p}_{\mathrm{T}}=2 \mathrm{~atm} \times \frac{3}{1}=6 \mathrm{~atm}\end{aligned}$

Hence, the answer is the option (1).

Example 5: A mixture of hydrogen and oxygen contains 40% hydrogen by mass when the pressure is 2.2 bar. The partial pressure of hydrogen is ____________ bar. (Nearest Integer)

1) 2

2)3

3)4

4)8

Solution

Let the mass of the mixture be 100 g

Mass of $\mathrm{H}_2$ gas = 40 g

Mass of $\mathrm{O}_2$ gas = 60 g

$\mathrm{NH}_2=\frac{40 \mathrm{~g}}{2 \mathrm{~g} / \mathrm{mol}}=20 \mathrm{~mole}$

$\begin{aligned} & \mathrm{NO}_2=\frac{60 \mathrm{~g}}{32 \mathrm{~g} / \mathrm{mol}}=1.875 \mathrm{~mole} \\ & \mathrm{X}_{\mathrm{H}_2}=\frac{20}{20+1.875}=0.91 \\ & \mathrm{P}_{\mathrm{H}_2}=\mathrm{X}_{\mathrm{H}_2} \quad \mathrm{P}_{\text {Total }}=0.91 \times 2.2 \mathrm{bar} \\ & \cong 26 \text { ar } \\ & \end{aligned}$

Hence, the answer is (2).

Summary

The partial pressure of each gas in a mixture is proportional to its mole fraction and can be computed using the following relation: Dalton's Law offers view that help to clearly understand and correctly predict what will happen with mixtures of gases. The law explains atmospheric pressure, that is how the combined individual gases in the atmosphere, nitrogen, oxygen, carbon dioxide, etc add up to give the total pressure.