The Deviation Of Real Gas From Ideal Gas Behavior

Introduction

Imagine you are in a crowded party. In case the number of people is small, everybody can move freely without bumping into one another significantly. Now this, in principle, would correspond to an ideal gas where gas molecules are far apart and don't interact significantly. As the party gets crowded, people start knocking into each other, forming groups, and their motion is restricted. This situation can be thought of as similar to what happens in a real gas. First, we need to have an ideal gas. That is to say, one in which the molecules of gas have no volume; moreover, there are no attractions and repulsions between them. This is the ideal limit, which holds very well in many conditions but does not hold in all. Actually, real gas molecules occupy space and are subject to forces exerted by others.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

This Story also Contains

1. Introduction
2. Ideal GasThese gases obey gas laws under all the conditions of temperature and pressure,
3. Real GasThese gases obey gas laws only at high temperatures and low pressure.
4. Explanations for Real Gas Behaviour
5. Summary

At high pressures, this forces the molecules closer together, and the volume becomes significant with respect to the total volume of the gas, resulting in a deviation from ideal behaviour. Similarly, at low temperatures, the motion of the molecules involved slows down, and the intermolecular attractive forces show up more obviously, further contributing to deviations. For example, take a balloon. As one blows it up, the air contained inside nearly acts as an ideal gas because the pressure is relatively low and the temperature is usual. However, if one continues inflating until tightened much, the air molecules will then be closer to each other, and the real gas behaviour becomes prominent.

Ideal Gas
These gases obey gas laws under all the conditions of temperature and pressure,

• No gas is ideal in reality (hypothetical).

• No force of attraction is present between molecules in them.

• The volume of molecules is negligible to the total volume of the gas (container).

Real Gas
These gases obey gas laws only at high temperatures and low pressure.

• All the gases are real.

• Here the force of attraction between molecules cannot be neglected at high pressure and low temperature.

• Here, the volume occupied by a gas molecule is not negligible, especially at high pressure and low temperature.

Behaviour of Real Gases: Deviation from Ideal Gas Behaviour and Compressibility factor Z

The extent of deviation of a real gas from ideal gas behaviour is expressed in terms of compressibility factor Z. It is an empirical correction for the non-ideal behaviour of real gases which allows the simple form of the combined gas law to be retained It is given as:
$\mathrm{Z}=\frac{\mathrm{PV}}{\mathrm{nRT}}$
When Z = 1 (ideal gas behaviour)

When Z < 1 (negative deviations)

When Z > 1 (positive deviations)

When Z < 1 gas is more compressible

When Z > 1 gas is less compressible

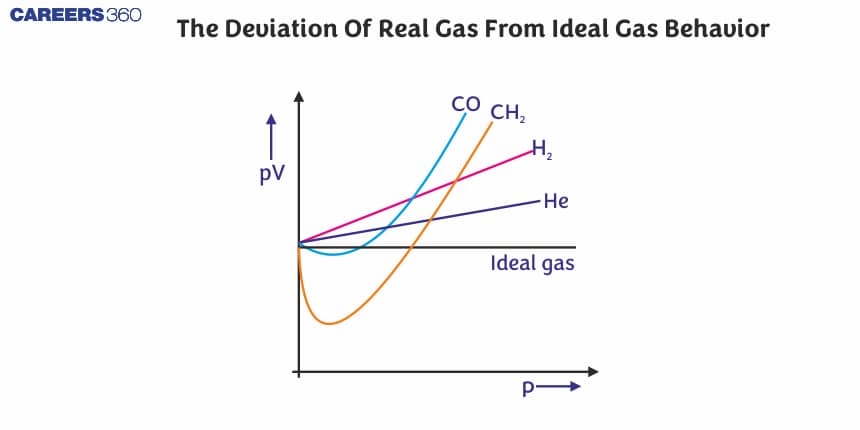
• For He and H₂ , Z > 1 as PV>RT [as a/V² = 0 ] that is positive deviations.
• At very Low Pressure: PV $\approx$ RT (as a/V² and b are neglected) that is, Z $\approx$ 1 so nearly ideal gas behaviour.
• At Low Pressure: PV<RT that is, Z < 1 so negative deviation
• At Moderate Pressure : PV = RT i.e, Z = 1 so ideal gas behaviour
• At High Pressure: PV > RT (as b can not be neglected). that is, Z > I so positive deviation.
• An increase in temperature shows a decrease in deviation from ideal gas behaviour.

Plot of pV vs p for real gas and ideal gas

Plot of pressure vs volume for real gas and ideal gas

Van der Waal’s Equation
Van der waal's equation is a modification of the ideal gas equation that takes into account the non-ideal behaviour of real gases Van der Waal 's equation modified kinetic theory of gases by considering these two points of the kinetic theory of gases not to be fully correct or are not followed by real gases.
For an ideal gas the force of attraction between gaseous molecules is negligible and the volume of gaseous molecules is negligible to the total volume of the gas. These two assumptiions are not followed by real gases.

He made the following two corrections :

• Volume Correction
  According to him, at high pressure the volume of the gas becomes lower so the volume of molecules can not be ignored Hence the actual space available inside the vessel for the movement of gas molecules is not the real volume of the gas, actually, it is given as:
  V_{real gas} = V - b
  Here V is the volume of the container while b is the volume occupied by gas molecules and it is called co-volume or excluded volume.
  The excluded volume for 'n' molecules of a gas = 4nV_m or (4 x 4/3?r³)
  Here V_m = Volume of one molecule (4/3?r³
  Thus, the ideal gas equation can be written as:
  P(V-nb) = nRT

• Pressure Correction
  According to him, the gaseous molecules are closer so attraction forces cannot be ignored hence, the pressure of the real gas is given as:
  The pressure of the Real gas = pressure developed due to collisions (P) + pressure loss due to attraction (p')
  $P_{\text {real gas }}=P+\mathrm{p}^{\prime}$
  Here p' is pressure loss due to force of attraction between molecules or inward pull
  As : $p^{\prime} \propto n^2,\left[n^2\right.$ is the number of molecules attracting or attracted $]$ $p^{\prime} \propto n^2 \propto d^2 \propto \frac{1}{V^2}$
  Thus, $\mathrm{p}^{\prime}=\frac{\mathrm{a}}{\mathrm{V}^2}=\frac{\mathrm{an}^2}{\mathrm{~V}^2}$ (for n moles of gas)
  Here 'a' is Van der Waal's force of attraction constant, d is density and V is volume.
  Hence$P_{\text {real gas }}=P+a / V^2$

$
\mathrm{P}_{\text {Real gas }}=\mathrm{P}+\frac{\mathrm{n}^2 \mathrm{a}}{\mathrm{V}^2} \ldots \ldots
$
(for n moles of gas)

• Now ideal gas equation can be written after correction of pressure and volume for n moles$\left(P+\frac{\mathrm{n}^2 a}{\mathrm{~V}^2}\right) \cdot(V-n b)=n R T$

• Units of a and b
  $\begin{aligned} & \mathrm{a}= \operatorname{lit}^2 \mathrm{~mol}^{-2} \mathrm{~atm} \\ & \text { or } \mathrm{cm}^4 \mathrm{~mol}^{-2} \text { dyne } \\ & \text { or } \mathrm{m}^4 \mathrm{~mol}^{-2} \text { Newton } \\ & \mathrm{b}= \text { lit } / \mathrm{mol} \\ & \text { or } \mathrm{cm}^3 / \mathrm{mol} \\ & \text { or } \mathrm{m}^3 / \mathrm{mol}\end{aligned}$
  The values of 'a' and 'b' are 0.1 to 0.01 and 0.01 to 0.001 respectively.

Variation of compressibility factor for some gases

Explanations for Real Gas Behaviour

• At very low pressure for one mole of a gas, the value of 'a' and 'b' can be ignored so Van der Waal's equation becomes equal to ideal gas.
  PV=RT
• At low pressure, the value of 'nb' or 'b' can be ignored so Van der Waal's equation becomes
  $\begin{aligned} & {\left[P+a / V^2\right][V]=R T} \\ & P V+\frac{a}{V}=R T \\ & P V=R T-\frac{a}{V}\end{aligned}$

  Hence PV < RT
  so,$\begin{aligned} & Z=\frac{P V}{R T} \\ & Z<1\end{aligned}$

• At moderate pressures, neither the value of 'a' nor 'b' can be neglected and we have to consider both the value of 'a' as well as 'b' for the calculation of Z.

• At high pressure, the value of 'a' can be ignored so Van der Waal's equation can be written as
  $
  \begin{aligned}
  & P(V-b)=R T \\
  & P V-P b=R T \\
  & P V=R T+P b \\
  & Z=\frac{P V}{R T}
  \end{aligned}
  $

• So, $Z>1$

For the better understanding of the topic The Deviation Of Real Gas From Ideal Gas Behavior ,watch the video:

Some Solved Examples

Example 1: A gas is said to behave like an ideal gas when the relation PV / T = constant. When do you expect a real gas to behave like an ideal gas?

1)When the temperature is low

2)When both the temperature and pressure are low

3)When both the temperature and pressure are high

4) When the temperature is high and pressure is low

Solution

At high temperatures and low pressure, the value of Z approaches unity.

Therefore, $P V=n R T$ is the ideal gas equation and it is followed by the real gas when the temperature is high and pressure is low.
Hence, the answer is the option (4).

Example 2: Gases deviate from the ideal gas behaviour because of their molecules:

1)Possess negligible volume

2) Have forces of attraction between them

3)Are polyatomic

4)Are not attracted to one another

Solution

As we learnt in the Behaviour of real gas - attraction forces exist between molecules at low temperatures.
Because molecules of real gases have intermolecular forces of attraction the effective impact on the wall of the container is diminished. The pressure of real gas is reduced by $\frac{a}{v^2}$ factor hence behaviour of real gas deviates from ideal behaviour.
Hence, the answer is the option (2).

Example 3: The pressure exerted by 5 moles of $\mathrm{CO}_2$ in one litre vessel at $47^{\circ} \mathrm{C}$ using Van der Waals equation is x atm while the pressure is y atm if it behaves ideally in nature. The value of x and y respectively are
(Given, $a=3.592 \mathrm{~atm} L^2 \mathrm{~mol}^{-2}$ , $b=0.0427 \mathrm{Lmol}^{-1}$ )

1)67.43 atm, 131.36 atm
2)77.21 atm, 134 atm

3)131.36 atm, 77.21 atm

4) 77.21 atm, 131.36 atm

Solution

We have:
V = 1 litre
T = 320K
a = 3.592
b = 0.0427
n = 5
Now, According to Van der Waals equation, we have:

$\left(P+\frac{a n^2}{V^2}\right)(V-n b)=n R T$

$\left(P+\frac{(5)^2 \times 3.592}{(1)^2}\right)(1-5 \times 0.0427)=5 \times 0.0821 \times 320$

$\Rightarrow \mathrm{P}=77.218 \mathrm{~atm}$

Thus, the pressure is 77.218 atm when the gas shows real gas behaviour. Now, if the gas behaves like an ideal gas, then, we know:

$\mathrm{PV}=\mathrm{nRT}$
$\Rightarrow \mathrm{P} \times 1=5 \times 0.0821 \times 320$$\Rightarrow \mathrm{P}=131.36 \mathrm{~atm}$

Thus, the pressure is 131.36 atm when the gas behaves ideally.
Hence, the answer is the option (4).

Example 4: The compressibility factor for 1 mole of a Vander Waal's gas at 0^oC and 100 atm pressure is found to be 0.5 then the V_real is -

1)0.224 L

2) 0.112 L

3)22.4 L

4)11.2 L

Solution

As we learnt in

Compressibility Factor -

$\begin{aligned} & Z=V_{\text {real }} / V_{\text {ideal }} \\ & P V_{\text {ideal }}=n R T \\ & V_{\text {ideal }}=\frac{n R T}{P}=\frac{1 \times 0.0821 \times 273}{100}=0.224 L \\ & Z=\frac{V_{\text {real }}}{V_{\text {ideal }}} \Rightarrow 0.5=\frac{V_{\text {real }}}{0.224} \\ & V_{\text {real }}=0.112 L\end{aligned}$

Hence, the answer is the option (2).

Summary

The two main reasons for which real gases vary from ideal behaviour are IMFs and the volume of the molecules of the gas. Real gases act completely differently from ideal gases; they have forces acting between their constituent molecules of attraction and repulsion, thus affecting their behaviour under varying conditions. Measurable deviations are more evident at high pressure and low temperature when the effect of the attractive forces between the molecules is much greater. These, in turn, may result in the deviation of the observed properties, like pressure, volume, and temperature, from what is expected from the ideal gas laws. Knowing these deviations is most important in chemistry, physics, and engineering not only to make predictions on the behaviour of gases but also to make proper designs of processes and to understand properly many natural phenomena.