• Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Difference Between Ideal Gas and Real Gas with FAQs

Difference Between Ideal Gas and Real Gas with FAQs

Team Careers360Updated on 02 Jul 2025, 04:55 PM IST

In this article, we will discuss the difference between real gas and ideal gas, non ideal gas, ideal and real gas, ideal and real gas examples.

Differentiate between ideal gas and real gas:

Ideal Gas
Real gas
Ideal gas has no definite volumeReal gas has definite volume
There are elastic collisions of particles in ideal gas.There is non - elastic collisions between particles in non-ideal gas.
There is absence of intermolecular attraction force in ideal gas.There is presence of intermolecular attraction force in real gas or non-ideal gas.
It does not exist in reality that is in the environment and is a hypothetical gas.It exists in the environment
The pressure is highThe pressure is less when compared to other ideal /perfect gas.
It is independentIt interacts with other gases.
It obeys gas laws such as pV=nRTIt obeys p + ((n2 a)/V2)(V - nb) = nRT

The above table gives the difference between real gas and ideal gas. So, we have assumed that all gases follow the gas laws under all conditions of temperature and pressure, however, this is not true for real gas. Difference between real gases and ideal gasis that real gas obeys the gas laws under limited conditions of low pressure and high temperature.

Theideal gas and real gas have major difference thatreal gases exhibit deviations from gaseous laws and the deviations increase when temperature and pressure are near to conditions in which the gas can condense into liquid, thus the Boyle’s and Charles’s law derived ideal gas equation is only applicable at relatively low pressure and moderately high temperatures.

NEET Highest Scoring Chapters & Topics
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download EBook

Also read -

Ideal gas and real gas difference are that ideal gas is a hypothetical gas that obeys the gas law exactly under all conditions of temperature and pressure which is perfect gas or ideal gas. The universal gas constant R, is an experimentally derived quantity which has the same value for all ideal gases.

Now, as we know that we can distinguish between ideal gas and real gas is that ideal gas equation pV= nRT, is not applicable to real gas, hence the evaluation of universal gas constant R cannot be done directly by using pressure, volume, and temperature data of real gas.

In ideal gas and real gas, we know through various experiments it is known that gases approach ideal behaviour as the pressure is decreased. Thus, the extrapolation method (p → 0) on the data of real gases can be utilized to determine the corresponding properties of ideal gas and hence the data gained from this method, after extrapolation, should be independent of the characteristic of the real gas used for experiment.

Here, ideal and real gas can be differentiated after calculating the volumes of one mole of a real gas at different pressures and constant temperature, a graph between pV and p can be drawn, then on extrapolating the graph to zero pressure and for departure from ideal behaviour it is now possible to determine the value of pV which is expected to be appropriate to one mole of ideal gas. By following this it is found that the value of (pV)p→0 at 273.15 K is 22.711 dm3 bar. Thus, if p=1 bar, then V=22.711 dm3. The volume occupied by one mole of an ideal gas at standard temperature 273.15 K and 1 bar pressure is 22.711 dm3.

In ideal gas and real gas, the difference between real and ideal gas is that real gas is the gases which do not obey the ideal gas laws exactly under all conditions of temperature and pressure and is also called as non-ideal gas. According to experiments at low pressure and moderately high temperature, the gases obey the laws of Boyle’s Charles and Avogadro approximately. But as the pressure rises or the temperature is decreased a visible departure from ideal behaviour is seen also a difference between ideal and non-ideal gas is seen. We can see the example of the type of deviation that occurs in Boyle’s law for H2 at room temperature.

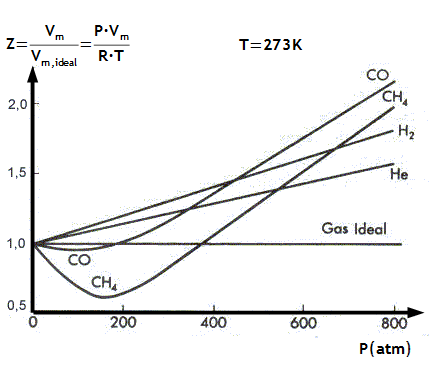
The deviations or the difference between ideal gas and real gas can be displayed more distinctively by plotting the graph with the ratio of the observed molar volume Vm to the ideal molar volume Vm ideal( = RT/p) as the function of pressure at constant temperature and this ratio is called the compression factor Z and this can be expressed as

Z = Vm/ Vm ideal = pVm/RT

The major difference between ideal gas and real gas is that for an ideal gas, Z = 1 and is independent of pressure and temperature. For example a real gas, Z = f(T,p) a function of both temperature and pressure as shown in figure below a graph between Z and p for some gases at 273.15 K, the inference we can conclude is that

File:Factor Z vs.png - Wikimedia Commons

Related Topics,

  1. Difference between ideal gas and real gas is that in real gas Z the compression factor is always greater than 1 for H2 because the attractive interactions are so weak that the repulsive interactions dominate even at low pressures.
  2. For CH4, at low pressure, Z is less than 1. That is, their molar volumes of the methane gas are smaller than that of a perfect gas, showing that the molecules are drawn together slightly and also, we can conclude that for these molecules and these conditions the attractive interactions are more dominant and this is the differentiate between real gas and ideal gas.

In the below figure, it gives the impression that the nature of deviations depends upon the nature of the gas. The more important determining factor is the temperature relative to the critical temperature of a selected/ particular gas which is near the critical temperature in real gas.

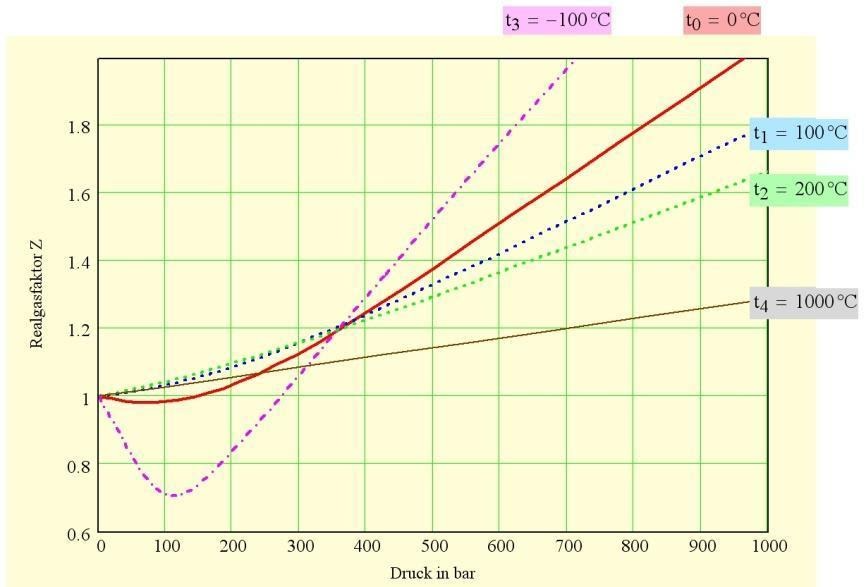
File:Realgasfaktor Stickstoff.jpg - Wikimedia Commons

Given the pressure is of the order of 1 bar or less, and the temperature is not too near the point of liquefaction, the observed deviations from the ideal gas laws are not more than a few % . Thus under these conditions, the equation pV =nRT and related expressions may be used. These are some of the examples of ideal gas and real gas.

The ideal gas differentiate from real gas or the difference between ideal gas and real gasis because ideal gas deviates from its ideal behaviour and this is because the ideal gas can be derived from the kinetic theory of gases which is based on the following two assumptions:

  1. The volume occupied by the molecules is negligible in comparison to the total volume of the gas in consideration.
  2. The molecules exert no forces of attraction on one another molecule.

As we know neither of these assumptions can be regarded as applicable to real gases that the latter show departure from the ideal gas behaviour.

The person who was the first to systematically introduce the correction terms due to the above two invalid assumptions in the ideal gas equation piVi = nRT was Van der Waals.

His corrections are

  1. Correction in Volume Vi = V – nb where b is excluded or co- volume.
  2. Correction for forces of attraction.

The equation which is applicable to all real gas is and is known as van der waals equation.

(p + n2a / V2) ( V- nb) = nRT

Thus, due to this, there is major difference between real and ideal gas.

Also, students can refer,

Also check-

NCERT Chemistry Notes:

Commonly Asked Questions

Q: What is the main difference between an ideal gas and a real gas?
A:
The main difference is that ideal gases are theoretical models that perfectly follow gas laws, while real gases are actual gases that deviate from these laws due to intermolecular forces and finite particle size. Ideal gases assume no intermolecular attractions and negligible particle volume, whereas real gases have these properties, leading to deviations from ideal behavior.
Q: Under what conditions do real gases behave most like ideal gases?
A:
Real gases behave most like ideal gases at high temperatures and low pressures. These conditions minimize intermolecular forces and the effect of particle volume, allowing real gases to more closely follow ideal gas laws. As temperature increases or pressure decreases, gas molecules have more space and energy, reducing interactions and behaving more ideally.
Q: What is the van der Waals equation, and how does it relate to real gases?
A:
The van der Waals equation is a modified version of the ideal gas law that accounts for the behavior of real gases. It introduces two constants: 'a' to account for intermolecular attractions, and 'b' to account for the volume of gas particles. This equation provides a more accurate description of real gas behavior, especially at high pressures and low temperatures where deviations from ideal behavior are more significant.
Q: How do intermolecular forces affect the behavior of real gases?
A:
Intermolecular forces cause real gas molecules to attract each other, leading to deviations from ideal gas behavior. These attractions can cause real gases to have a lower pressure than predicted by the ideal gas law at the same volume and temperature. The effect is more pronounced at lower temperatures and higher pressures, where molecules are closer together and interactions are stronger.
Q: Why do real gases deviate more from ideal behavior at high pressures?
A:
At high pressures, real gas molecules are forced closer together, increasing the significance of both intermolecular forces and the volume occupied by the gas particles. This leads to greater deviations from ideal gas behavior. The assumptions of negligible particle volume and no intermolecular interactions in the ideal gas model become less valid under these conditions.

Frequently Asked Questions (FAQs)

Q: How do real gases behave differently from ideal gases in terms of their Joule-Thomson coefficient?
A:
The Joule-Thomson coefficient describes how the temperature of a gas changes during an isenthalpic expansion. For an ideal gas, this coefficient is zero, meaning no temperature change occurs. Real gases, however, can have positive or negative Joule-Thomson coefficients, leading to cooling or heating during expansion. This behavior is due to intermolecular forces and varies with temperature and pressure, playing a crucial role in processes like gas liquefaction.
Q: How do real gases behave differently from ideal gases in terms of effusion and diffusion rates?
A:
While Graham's law of effusion and diffusion applies to both ideal and real gases, real gases can show slight deviations. In ideal gases, these rates depend solely on molecular mass. For real gases, intermolecular forces and molecular size can affect these rates, especially at high pressures or low temperatures. Larger molecules or those with stronger intermolecular attractions may diffuse or effuse more slowly than predicted by Graham's law.
Q: How do real gases behave differently from ideal gases during isothermal compression?
A:
During isothermal compression, real gases deviate from the behavior predicted by Boyle's law for ideal gases. At high pressures, real gases are generally less compressible than ideal gases due to the finite volume of molecules and repulsive forces. At moderate pressures, some real gases may be more compressible due to attractive forces. These deviations become more pronounced as the gas approaches its critical point or liquefaction.
Q: How does the heat capacity of a real gas differ from that of an ideal gas?
A:
The heat capacity of a real gas can differ from that of an ideal gas due to intermolecular forces. In an ideal gas, heat capacity depends only on the gas's degrees of freedom. In real gases, additional energy can be stored in intermolecular potentials, leading to a heat capacity that varies with temperature and pressure. This difference is more pronounced at low temperatures or high pressures where intermolecular interactions are more significant.
Q: What is the Joule-Thomson effect, and how does it differ between ideal and real gases?
A:
The Joule-Thomson effect is the temperature change that occurs when a gas expands at constant enthalpy. In an ideal gas, this effect is zero – the temperature doesn't change during expansion. However, real gases can experience either cooling or heating during this process, depending on their initial temperature and pressure. This difference arises from the intermolecular forces present in real gases but absent in ideal gases.
Q: What is the significance of the Boyle-Mariotte law for real gases?
A:
The Boyle-Mariotte law states that for an ideal gas at constant temperature, pressure and volume are inversely proportional. For real gases, this law holds approximately at low pressures and high temperatures. Deviations from this law at high pressures or low temperatures indicate the presence of intermolecular forces and finite molecular volume in real gases. Understanding these deviations is crucial for accurate predictions of real gas behavior.
Q: How do real gases behave differently from ideal gases during Joule expansion?
A:
In Joule expansion, a gas expands into a vacuum. For an ideal gas, there's no temperature change during this process. However, real gases can experience temperature changes due to intermolecular forces. Most real gases cool slightly during Joule expansion (except at very high temperatures), while ideal gases maintain constant temperature. This difference highlights the impact of intermolecular attractions in real gases.
Q: What is the Maxwell-Boltzmann distribution, and how does it apply differently to ideal and real gases?
A:
The Maxwell-Boltzmann distribution describes the distribution of molecular speeds in a gas at thermal equilibrium. For ideal gases, this distribution depends only on temperature and molecular mass. In real gases, intermolecular forces can affect the distribution, especially at high pressures or low temperatures. This leads to slight deviations in the actual speed distribution compared to what the ideal Maxwell-Boltzmann distribution predicts.
Q: How does the speed of sound in a real gas differ from that in an ideal gas?
A:
The speed of sound in a real gas can differ from that in an ideal gas due to the effects of intermolecular forces and finite particle size. In an ideal gas, the speed of sound depends only on temperature and the gas's molecular weight. In real gases, it can also be affected by pressure and the gas's compressibility. This difference becomes more pronounced at high pressures or low temperatures where real gas effects are more significant.
Q: What is the significance of the Boyle point in understanding real gas behavior?
A:
The Boyle point is the temperature at which the second virial coefficient of a gas becomes zero. At this point, the gas behaves most like an ideal gas over a range of pressures. The Boyle point is significant because it represents a condition where the attractive and repulsive forces between gas molecules effectively cancel out, allowing the gas to follow the ideal gas law more closely. It's a useful reference point for understanding real gas behavior.
Articles
Previous
Next