Equilibrium constant

The concept of equilibrium constant was developed by the work of various scientists. Cato Maximilian Gulberg and Peter Waage as they worked on the law of mass action they are also working on the concept of the equilibrium constant in their formulation they proposed the rate of reaction is proportional to the concentration of the reactant and at equilibrium the ratio of the concentration of product to reactant is constant. Further another scientist Jacobus Henricus Vant Hoff developed the theory by relating the equilibrium constant to the temperature and predicting the impact of temperature change on the position of equilibrium.

Equilibrium Constant

It is the ratio of the rate of forward and backward reaction at a particular temperature or it is the ratio of active masses of the reactants to that of active masses of products at a particular temperature raised to their stoichiometric coefficients. It is denoted by K_c or K_p. The distinction between K_eq and K_c is that the expression of K_eq involves all the species (whether they are pure solids, pure liquids, gases, solvents or solutions) while the expression K_c involves only those species whose concentration is a variable (gases and solution). It means K_c is a devoid of pure components (like pure solids and pure liquids) and solvents.

Let us look at the definition of Equilibrium constant in terms of concentration and partial pressure

(1) Equilibrium constant in Terms of Concentration

For a reaction:

$\begin{aligned} & \mathrm{mA}+\mathrm{nB} \rightleftharpoons \mathrm{pC}+\mathrm{qD} \\ & \mathrm{r}_{\text {forward }} \propto[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}=\mathrm{K}_{\mathrm{f}}[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}} \\ & \mathrm{r}_{\text {backward }} \propto[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}=\mathrm{K}_{\mathrm{b}}[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}\end{aligned}$

We know that at equilibrium

$\begin{aligned} & \mathrm{r}_{\mathrm{f}}=\mathrm{r}_{\mathrm{b}} \\ & \mathrm{K}_{\mathrm{f}}[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}=\mathrm{K}_{\mathrm{b}}[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}} \\ & \frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}=\frac{[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}}{[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}} \quad \text { (at constant temperature) } \\ & \frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}=\frac{[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}}{[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}}=\mathrm{K}_{\mathrm{c}}\end{aligned}$

The above expression gives us the value of Kc as the activity or the active mass is expressed in terms of the concentrations (c) or the molarity

(2) Equilibrium constant in terms of Partial pressure

In this case, the equilibrium constant is known as K_p. It is applicable only for gaseous systems.
For the reaction:
$\begin{aligned} & \mathrm{mA}+\mathrm{nB} \rightleftharpoons \mathrm{pC}+\mathrm{qD} \\ & \mathrm{r}_{\text {forward }} \propto \mathrm{P}_{\mathrm{A}}^{\mathrm{m}} \mathrm{P}_{\mathrm{B}}^{\mathrm{n}}=\mathrm{K}_{\mathrm{f}_1} \mathrm{P}_{\mathrm{A}}^{\mathrm{m}} \mathrm{P}_{\mathrm{B}}^{\mathrm{n}} \\ & \mathrm{r}_{\text {backward }} \propto \mathrm{P}_{\mathrm{C}}^{\mathrm{p}} \mathrm{P}_{\mathrm{D}}^{\mathrm{q}}=\mathrm{K}_{\mathrm{b}_1} \mathrm{P}_{\mathrm{C}}^{\mathrm{p}} \mathrm{P}_{\mathrm{D}}^{\mathrm{q}}\end{aligned}$

At equilibrium

$\begin{aligned} & \mathrm{r}_{\mathrm{f}}=\mathrm{r}_{\mathrm{b}} \\ & \mathrm{K}_{\mathrm{f}_1} \mathrm{P}_{\mathrm{A}}^{\mathrm{m}} \mathrm{P}_{\mathrm{B}}^{\mathrm{n}}=\mathrm{K}_{\mathrm{b}_1} \mathrm{P}_{\mathrm{C}}^{\mathrm{p}} \mathrm{P}_{\mathrm{D}}^{\mathrm{q}} \\ & \mathrm{K}_{\mathrm{P}}=\frac{\mathrm{K}_{\mathrm{f}_1}}{\mathrm{~K}_{\mathrm{b}_2}}=\frac{\mathrm{P}_{\mathrm{C}}^{\mathrm{p}} \mathrm{P}_{\mathrm{D}}^{\mathrm{q}}}{\mathrm{P}_{\mathrm{A}}^{\mathrm{m}} \mathrm{P}_{\mathrm{B}}^{\mathrm{n}}}\end{aligned}$

The above expression gives us the value of K_P as the activity is expressed in terms of partial pressures.

Note: This is generally used for gaseous systems or systems where gases are in equilibrium with liquids or solids

Recommemded topic video on (Equilibrium constant)

Some Solved Examples

1.The equilibrium constant (K_C) for the reaction $\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NO}(\mathrm{g})$ at temperature T is $4 \times 10^{-4}$. The value of K_C for the given reaction at the same temperature is :

$\mathrm{NO}(\mathrm{g}) \rightarrow \frac{1}{2} \mathrm{~N}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g})$

1)0.02

2)2.5 x 10 ²

3)4 x 10 ^-4

4) (correct)50

Solution

As we discussed in the concept

The equilibrium constant for the reverse reaction -

The equilibrium constant for the reverse reaction is the inverse of the equilibrium constant for the reaction in the forward direction.

$\begin{aligned} & \mathrm{N}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})} \rightarrow 2 \mathrm{NO}_{(\mathrm{g})} \rightarrow(\mathrm{i}) \\ & \mathrm{K}_{\mathrm{c}}=4 \times 10^{-4}\end{aligned}$

By multiplying the equation (i) by $\frac{1}{2}$

$\begin{aligned} & \frac{1}{2} \mathrm{~N}_{2(\mathrm{~g})}+\frac{1}{2} \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{NO}_{(\mathrm{g})} \rightarrow \text { (ii) } \\ & \mathrm{K}_{\mathrm{c}}^{\prime}=\sqrt{\mathrm{K}_{\mathrm{c}}}=\sqrt{4 \times 10^{-4}}=2 \times 10^{-2}\end{aligned}$

By reversing the equation (ii), we get

$\mathrm{NO}_{(\mathrm{g})} \rightarrow \frac{1}{2} \mathrm{~N}_{2(\mathrm{~g})}+\frac{1}{2} \mathrm{O}_{2(\mathrm{~g})} \mathrm{K}_{\mathrm{c}}^{\prime \prime}=\frac{1}{\mathrm{~K}_{\mathrm{c}}^{\prime}}=\frac{1}{2 \times 10^{-2}}=50$

Hence, the answer is the option (4).

2. A vessel at 1000 K contains CO₂ with a pressure of 0.5 atm. Some of the CO₂ is converted into CO on the addition of graphite. If the total pressure at equilibrium is 0.8 atm, the value of K is

1) (correct)1.8 atm

2)3 atm

3)0.3 atm

4)0.18 atm

Solution

Given,

$\mathrm{CO}_{2(\mathrm{~g})}+\mathrm{C}_{(\mathrm{s})} \leftrightharpoons 2 \mathrm{CO}_{(\mathrm{g})}$

Initial pressure 0.5 atm 0 0

Pressure at equilibrium 0.5-x 2x

Total Pressure = 0.5 - x + 2x = 0.8

x = 0.3

$\begin{aligned} & k=\frac{(p C O)^2}{\left(p C O_2\right)} \\ & k=\frac{(0.6)^2}{0.2} \\ & =1.8 \mathrm{~atm}\end{aligned}$

Hence, the answer is the option (1)

3 .Solid ammonium carbamate dissociates to give ammonia and carbon dioxide as follows. $\mathrm{NH}_2 \mathrm{COONH}_{4(\mathrm{~s})} \rightleftharpoons 2 \mathrm{NH}_{3(\mathrm{~g})}+\mathrm{CO}_{2(\mathrm{~g})}$ At equilibrium, ammonia is added such that partial pressures of NH₃ now equals the original total pressure. Calculate the ratio of the total pressure now to the original total pressure.

1) (correct)$\frac{31}{27}$

2)$\frac{60}{40}$

3)$\frac{31}{9}$

4)$\frac{62}{27}$

Solution

The reaction:-

Initial $\mathrm{NH}_2 \mathrm{COONH}_{4(\mathrm{~s})} \rightleftharpoons \underset{2 \mathrm{P}}{2 \mathrm{NH}_{3(\mathrm{~g})}}+\underset{\mathrm{P}}{\mathrm{CO}_{2(\mathrm{~g})}}$

$\begin{aligned} & \mathrm{K}_{\mathrm{p}}=\left(\mathrm{P}_{\mathrm{NH}_3}\right)^2\left(\mathrm{P}_{\mathrm{CO}_2}\right) \\ & \mathrm{P}_{\mathrm{T}}(\text { initial })=3 \mathrm{P} \\ & \quad \mathrm{NH}_2 \mathrm{COONH}_{4(\mathrm{~s})} \rightleftharpoons 2 \mathrm{NH}_{3(\mathrm{~g})}+\mathrm{CO}_{2(\mathrm{~g})} \\ & \text { Initial } \\ & \mathrm{K}_{\mathrm{P}}=(3 \mathrm{P})^2\left(\mathrm{P}^{\prime}\right) \quad \ldots \ldots \ldots \ldots \text { (ii) }\end{aligned}$

From eq (I) and (ii)

$\begin{aligned} & (2 \mathrm{P})^2(\mathrm{P})=(3 \mathrm{P})^2\left(\mathrm{P}^{\prime}\right) \\ & \mathrm{P}^{\prime}=\frac{4 \mathrm{P}}{9}\end{aligned}$

$\frac{\mathrm{P}_{\mathrm{T}}(\text { new })}{\mathrm{P}_{\mathrm{T}}(\text { old })}=\frac{3 \mathrm{P}+\mathrm{P}^{\prime}}{3 \mathrm{P}}=\frac{3 \mathrm{P}+\frac{4 \mathrm{P}}{9}}{3 \mathrm{P}}=\frac{31}{27}$

Hence, the answer is the option (1).

4. For the hypothetical reactions, the equilibrium constant (K) values are given:

$\mathrm{A} \rightleftharpoons \mathrm{B} ; \mathrm{K}_1=2 ; \quad \mathrm{B} \rightleftharpoons \mathrm{C} ; \mathrm{K}_2=4 ; \quad \mathrm{C} \rightleftharpoons \mathrm{D} ; \mathrm{K}_3=3$
The equilibrium constant (K) for the reaction $A \rightleftharpoons D$ is:

1)12

2) (correct)24

3)6

4)9

Solution

The required reaction $A \rightleftharpoons D$ can be obtained by adding all the given reactions

We know that the Equilibrium constants get multiplied when the equations are added

$\begin{aligned} & \therefore \mathrm{K}=\mathrm{K}_1 \times \mathrm{K}_2 \times \mathrm{K}_3 \\ & \Rightarrow \mathrm{K}=2 \times 4 \times 3=24\end{aligned}$

Hence, the answer is the option (2).

5 .Value of equilibrium constant depends upon:

1)Temperature

2)Method of expressing activity or active mass

3) (correct)Both 1 and 2

4)Volume

Solution

Equilibrium constants are changed if you change the temperature of the system. Kc or Kp is constant at a constant temperature, but they vary as the temperature changes.

• The equilibrium constant K is determined by the activities of the components in the equilibrium expression.

• The values of Kc and Kp can be different in magnitude as well as dimensions.

Hence, the answer is the option (3).

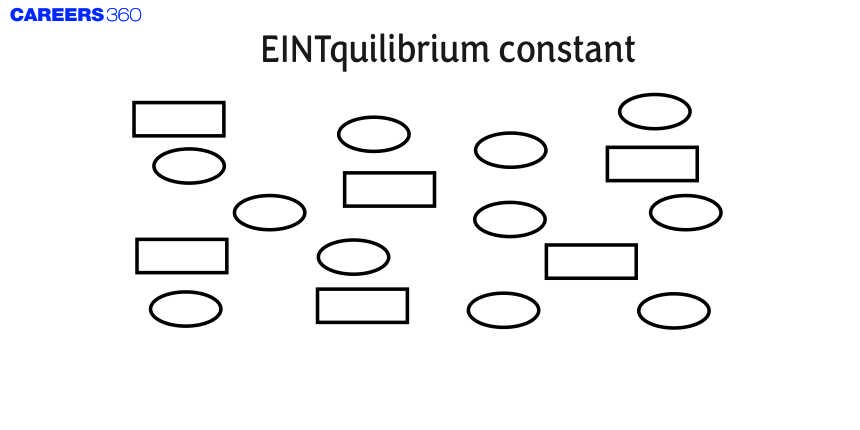
6 .In the figure shown below reactant A (represented by a square) is in equilibrium with product B (represented by a circle). The equilibrium constant is :

1)1

2)4

3)8

4) (correct)2

Solution

Now,

$A \leftrightharpoons B$

$K_c=\frac{[B]}{[A]}$

The concentration of [B] as represented by circle = 11

and the concentration of [A] as represented by square = 6

Therefore, the value of the equilibrium constant is near 2.

Hence, Option number (4) is c

7.For the following three reactions (i), (ii) and (iii), equilibrium constants are given

(i) $\mathrm{CO}_{(\mathrm{g})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{2(\mathrm{~g})}+\mathrm{H}_{2(\mathrm{~g})} ; \mathrm{K}_1$
(ii) $\mathrm{CH}_{4(\mathrm{~g})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{(\mathrm{g})}+3 \mathrm{H}_{2(\mathrm{~g})} ; \mathrm{K}_2$
(iii) $\mathrm{CH}_{4(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{2(\mathrm{~g})}+4 \mathrm{H}_{2(\mathrm{~g})} ; \mathrm{K}_3$

Which of the following relation is correct ?

1)$\mathrm{K}_3 \cdot \mathrm{K}_2^3=\mathrm{K}_1^2$

2)$\mathrm{K}_1 \sqrt{\mathrm{K}_2}=\mathrm{K}_3$

3)$\mathrm{K}_2 \mathrm{~K}_3=\mathrm{K}_1$

4) (correct)$\mathrm{K}_3=\mathrm{K}_1 \mathrm{~K}_2$

Solution

$\begin{aligned} & \mathrm{CO}_{(\mathrm{g})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{2(\mathrm{~g})}+\mathrm{H}_{2(\mathrm{~g})} \\ & \mathrm{K}_1=\frac{\left[\mathrm{CO}_2\right]\left[\mathrm{H}_2\right]}{[\mathrm{CO}]\left[\mathrm{H}_2 \mathrm{O}\right]} \ldots \ldots \ldots . .(\mathrm{i}) \\ & \mathrm{CH}_{4(\mathrm{~g})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{(\mathrm{g})}+3 \mathrm{H}_{2(\mathrm{~g})} \\ & \mathrm{K}_2=\frac{[\mathrm{CO}]\left[\mathrm{H}_2\right]^3}{\left[\mathrm{CH}_4\right]\left[\mathrm{H}_2 \mathrm{O}\right]} \ldots \ldots \ldots . .(\text { ii }) \\ & \mathrm{CH}_{4(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})} \rightleftharpoons \mathrm{CO}_{2(\mathrm{~g})}+4 \mathrm{H}_{2(\mathrm{~g})} \\ & \mathrm{K}_3=\frac{\left[\mathrm{CO}_2\right]\left[\mathrm{H}_2\right]^4}{\left[\mathrm{CH}_4\right]\left[\mathrm{H}_2 \mathrm{O}\right]^2} \ldots \ldots \ldots .(\text { iii })\end{aligned}$

From equations (i), (ii) and (iii); $\mathrm{K}_3=\mathrm{K}_1 \times \mathrm{K}_2$

Hence, the answer is the option (4).

Summary

The equilibrium constant has several applications in our lives it impacts our lives by various means such as in the environment it is used to control pollution as it is used to design the system for our air and water purification by optimizing conditions to remove pollutants effectively. It is also used for drug formulation as an equilibrium constant used to design and optimize drug formulation, ensuring that medications are effective and stable. it also helps in understanding the process of how drugs interact with the body. It is also used as a preservative in the food industry. Equilibrium constants have also used process like fermentation and canning to control and optimize reactants that preserve food and enhance flavour.