Partial Pressure - Dalton’s Law, Application, Formula, Units, FAQs

After reading this article, the reader should be able to answer the following questions:- how to calculate partial pressure, how to find partial pressure experimentally, what is partial pressure.

Keywords - partial pressure, partial pressure units, partial pressure meaning, partial pressure formula, partial pressure of the gas.

• Partial pressure is the pressure exerted by an individual gas present in a mixture of gases provided that the gases should be non-reactive.

• The partial pressure of an individual gas is determined by a formula

p_n=X_np_total

Partial Pressure-

The physical state of the gaseous state can be described by quantities like volume, pressure, and temperature. The origin of the term “Atmospheric Pressure” is from the fact that the pressure we are talking about is exerted by Earth’s atmosphere. The gravity of Earth pulls air toward its surface which develops pressure on the earth’s surface. This is how pressure develops on the Earth’s surface. One of the main characteristics of air is that it exerts pressure in all directions in the same quantity. The First Gas law given by Boyle, established an inverse relationship between pressure and volume and Gay Lussac’s Law gave a direct relationship between pressure and temperature.

• Partial Pressure definition- Partial Pressure is defined as the pressure exerted by an individual gas in a mixture of non-reactive gases.

• Partial pressure meaning is that pressure which is not total but only the pressure of an individual gas is taken out of the total pressure of mixed gases. This pressure is called partial pressure.

• The partial balancing means balancing partially reciprocating masses.

Also read -

• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for All Subjects

Dalton’s Law of Partial Pressure-

• Dalton was the first scientist to state that the pressure of gas doesn’t depend on the nature of the gas. Just how pure gases obey gas laws, a mixture of gases also obey gas laws i.e., gas laws apply to oxygen as well as air.

• Each non-reacting gas present in the air contributes to the total pressure in proportion to a fraction (in moles). This contribution of each gas is known as the partial pressure of the gas.

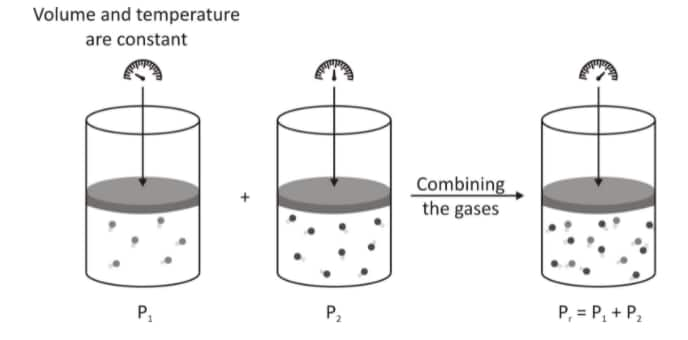
• Dalton stated that the total pressure of a non-reactive gaseous mixture will be equal to the sum of partial pressure of each gas.

• Ptotal is the total pressure of the gases and p₁, p₂, p₃ .. are the partial pressure of each gas. Partial pressure is the same pressure exerted by an individual gas if the gas is contained in a jar of the same volume and temperature.

• Dalton’s law of partial pressure is not applicable to the mixture of gases that reacts with each other.

Application of Dalton’s Law of Partial pressure of gas-

• The pressure of gases over the surface of the liquid can be calculated by using Dalton’s Law of partial pressure. The total pressure of a mixture of gas and water will be equal to atmospheric pressure if the water level inside and outside the vessel are equal.

• The gas present over water exerts combined pressure due to its vapor pressure and due to the pull of gravity. This gas contains water vapors. The pressure of dry gas can be calculated easily using the following equation.

When the level of water gets equal on the inside and outside-

P_atm=P_total

P_total=P_gas+P_water

P_gas=P_atm-P_water

P_water=Aqueous tension

Fig- Pressure measurement of gas over the surface of the water.

The vapor pressure of a gas is different at a different temperature, therefore, P_water is known.

Aqueous tension is the pressure exerted by water vapors. This Aqueous tension is the vapor pressure. Vapor pressure is the pressure exerted by the vapors of the liquid. Above the surface of a liquid, there always exists vapors of that liquid which exist in equilibrium with the water.

Dalton’s law of partial pressure applicability-

Dalton set a restriction for gases obeying Dalton’s law of partial pressure.

• Gases of the mixture should not react with each other. Some gases like ammonia (NH₃ and HCl) react with each other to form products like ammonium chloride (NH₃Cl). Therefore, Dalton's law of partial pressure does not apply to such gases.

• Similarly, gases like Hydrogen(H₂) and chlorine (Cl₂) react to form hydrogen chloride (HCl).

Partial pressure formula-

Let there be a container with gas A and gas B inside it. Gas A and Gas B will have partial pressure p_a and p_b.

According to the ideal gas equation-

p_a=n₁RT/V

And p_b=n₂RT/V

Here, n₁ and n₂ are numbers of moles of gases present in the container.

the total pressure of a mixture of two gases is given by-

p_total=p₁+p₂

=n₁ RT/V+n₂ RT/V

=(n₁+n₂) RT/V

Dividing p₁ by p_total-

p_1/p_total=(n₁/n₁+n₂) RTV/RTV

n₁/n₁+n₂= n₁/n₂= X₁

Where X₁ is the mole fraction of the first Gas.

p₁=X₁ p_total

For both gases A and B,

The general equation can be written as-

p_n=X_n p_total

This is the formula of partial pressure of any gas.

Where p_n is the partial pressure of nth gas and x_n is the partial pressure of n^th gas.

Also Read:

• NCERT solutions for Class 12 Chemistry Chapter 2 Solutions
• NCERT Exemplar Class 12 Chemistry Solutions Chapter 2 Solutions
• NCERT notes Class 12 Chemistry Chapter 2 Solutions

Units of Partial Pressure-

Partial pressure units are the same as the units of normal pressure.

• The barometer is the instrument used in the lab to measure the pressure. The height of mercury determines the atmospheric units.

• The barometer is assembled using a glass tube. This glass tube is closed from one end and open from the other end. Glass tube is filled with pure mercury. Glass tube is inverted into an open vessel containing mercury. The level of mercury drops until the atmospheric pressure acting outside the glass tube becomes equal to the pressure inside the tube.

• If the height of the column decreases then atmospheric pressure increases and if the height of the column increases then the atmospheric pressure decreases.

It is the maximum height of mercury that determines the pressure. The height keeps falling and raising due to the changes from time to time.

Consider mercury-filled in an inverted glass tube of h cm and area of cross-section be equal to a cm²

We know that

pressure=force/area

Force=mass×acceleration

pressure=mass×acceleration/area

P=mg/A

P=d×V×g/A

P=d×A×h×g/A

=hdg

where d is the density, h is the height, g is the gravity and A is the area.

1 atm is that pressure which supports a mercury height of 76 cm at 0°C

Also check-

• NCERT Exemplar Class 11th Chemistry Solutions
• NCERT Exemplar Class 12th Chemistry Solutions
• NCERT Exemplar Solutions for All Subjects

NCERT Chemistry Notes:

• NCERT Notes Class 11th Chemistry
• NCERT Notes Class 12th Chemistry
• NCERT Notes For All Subjects