Conic Sections- Parabola, Ellipse , Hyperbola with Examples
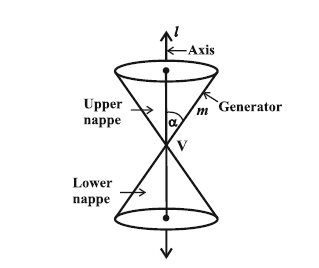
The two-dimensional curves that can be generated as cross-sections when a double cone is cut by a plane at different angles are called conic sections. The four curves - circle, parabola, ellipse, and hyperbola are called conic sections because they can be formed by interesting a double right circular cone with a plane. In real life, we use Parabolas in bridges and satellites, orbital mechanisms, and optics.
This Story also Contains
- What is a Conic Section?
- Conic Section in 2-dimensions: Definition
- Equation of Conic Section:
- Recognition of Conics
- Solved Examples Based on Conic Sections
- Summary
In this article, we will cover the concept of Pair of straight lines. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of twenty questions have been asked on JEE MAINS( 2013 to 2023) from this topic.
What is a Conic Section?
The two-dimensional curves that can be generated as cross-sections when a double cone is cut by a plane at different angles are called conic sections.
We obtain different kinds of conic sections depending on the position of the intersecting plane with respect to the cone and by the angle made by it with the vertical axis of the cone.
Let $\beta$ be the angle made by the intersecting plane with the vertical axis of the cone
For example, parabola, ellipse, and hyperbola are conic sections as they are formed when a plane cuts a double cone as shown in the figure

Note: a circle is a special case of ellipse when the plane is perpendicular to the axis of the double cone, and hence a circle is also a conic section
Conic Section in 2-dimensions: Definition
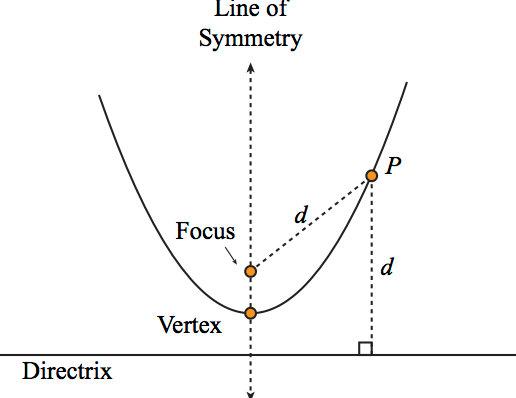
A conic section is the locus of a point that moves in a plane so that its distance from a fixed point is in a constant ratio to its perpendicular distance from a fixed-line.
The fixed point is called the Focus of the conic and this fixed line is called the Directrix of the conic.
Also, the constant ratio is called the Eccentricity and is denoted by e.
From the figure

$\begin{aligned}
& \frac{\mathrm{PS}}{\mathrm{PM}}=\text { constant }=\mathrm{e} \\
\Rightarrow \quad & \mathrm{PS}=\mathrm{e} \cdot \mathrm{PM}
\end{aligned}$
Conic Section Parameters
Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.
Vertex: The point of intersection of the conic section and the axis is called the vertex of the conic section.
Double ordinate: Any chord, that is perpendicular to the axis of the conic section, is called a double ordinate of the conic section.
Focal chord: Any chord passing through the focus is called the focal chord of the conic section.
Focal distance: The distance between the focus and any point on the conic is known as the focal distance of that point.
Latus rectum: Any chord passing through the focus and perpendicular to the axis is known as the latus rectum of the conic section.
Centre: The point which bisects every chord of the conic passing through it, is called the centre of the conic section.
Equation of Conic Section:

$
\begin{aligned}
&\text { The focus at } S(h, k) \text { and the Directrix : } a x+b y+c=0 \text {, then equation of conix }\\
&\begin{aligned}
& \Rightarrow P S=e \cdot P M \\
& \Rightarrow \sqrt{(x-h)^2+(y-k)^2}=e \cdot \frac{|a x+b y+c|}{\sqrt{a^2+b^2}} \\
& \Rightarrow(x-h)^2+(y-k)^2=e^2 \cdot \frac{(a x+b y+c)^2}{a^2+b^2}
\end{aligned}
\end{aligned}
$
Recognition of Conics
Equation of conic represented by the general equation of second-degree
$
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0
$
The discriminant of the above equation is denoted by $\Delta$, where
$
\Delta=a b c+2 f g h-a f^2-b g^2-c h^2
$
It can also be written in determinant form as
$\left|\begin{array}{lll}a & h & g \\ h & b & f \\ g & f & c\end{array}\right|$
Case 1: When the focus lies on the directrix
\begin{equation}
\Delta=0 \text { : In this case, the equation represents a pair of straight lines }
\end{equation}
Case 2: When the focus does not lie on the directrix
| Form: | $y^2=4 a x$ | $y^2=-4 a x$ | $x^2=4 a y$ | $x^2=-4 a y$ |
| Vertex | $(0,0)$ | $(0,0)$ | $(0,0)$ | $(0,0)$ |
| Focus | $(a, 0)$ | $(-a, 0)$ | $(0, a)$ | $(0,-a)$ |
| Equation of the directrix | $x=-a$ | $x=a$ | $y=-a$ | $y=a$ |
| Equation of the axis | $y=0$ | $y=0$ | $x=0$ | $x=0$ |
| Length of the latus rectum | $4a$ | $4a$ | $4a$ | $4a$ |
Recommended Video Based on Conic Sections
Solved Examples Based on Conic Sections
Example 1:What is the shape we get when we slice a double-napped cone parallel to the x-y plane and not on the vertex?
Solution: We know that Double napped circular cone. -Vertex separates the cone into two parts called nappes
So we get a circle in this case

Example 2: What happens when the plane cuts at an angle of $\beta=90^{\circ}$ but at the vertex?
Solution Different conic sections - We get a circle. when $\beta=90^{\circ}$

It is clear that when $\beta=90^{\circ}$, we will get a circle, but at the vertex, we get a point circle i.e a point

Hence, the answer is a circle
Example 3: Which conic do we get when $\beta=35^{\circ}$ and $\alpha=25^{\circ}$ ?
Solution: We know that Different conic sections -We get an ellipse when $\alpha<\beta<90^{\circ}$

When $\alpha<\beta<90^{\circ}$
Then we get an ellipse
hence, the answer is an ellipse
Example 4: What will happen if $\alpha=\beta=30^{\circ}$ and we cut the double napped come with a plane?
Solution we know that Different conic sections - We get a parabola, when $\beta=\alpha$

When $\beta=\alpha$; we get a parabola
Hence, the answer is Parabola
Example 5 : What are the coordinates of the focus of the parabola
$
y^2+6 y-4 x+2=0
$
Solution: We know that Focus - The fixed point of a conic section
$ \begin{aligned}
& y^2+6 y+9=4 x-2+9 \\
& (y+3)^2=4 x+7=4\left(x+\frac{7}{4}\right)
\end{aligned}$
Thus the point vertex is $\left(\frac{-7}{4},-3\right)$
Thus focus will be $\left(\frac{-7}{4}+1,-3\right)$
$
=\left(\frac{-3}{4},-3\right)
$
Hence, the answer is $\left(\frac{-3}{4},-3\right)$
Summary
The conic section represents a versatile family of curves. It represents a deep knowledge of the different varieties of curves, their equations, and their properties. Moreover, the study of conic sections extends beyond their practical applications; it also tells about symmetry and curvature.
Frequently Asked Questions (FAQs)
Equation of conic represented by the general equation of second-degree $\mathrm{ax}^2+2 \mathrm{hxy}+\mathrm{by}^2+2 g \mathrm{x}+2 \mathrm{fy}+\mathrm{c}=0$
When the focus lies on the directrix $\Delta=0$. In this case, the equation represents a pair of straight lines.
The two-dimensional curves that can be generated as cross-sections when a double cone is cut by a plane at different angles are called conic sections.
The point of intersection of the conic section and the axis is called the vertex of the conic section.
Any chord passing through the focus and perpendicular to the axis is known as the latus rectum of the conic section.