Derivative of a Function

A derivative of a function is obtained by differentiating it. Derivative of a function is a crucial concept in Calculus. It is the basics for all the complex problems in calculus. These concepts of differentiation have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Function:
2. Derivative of a Function
3. Higher Order Derivative of a Function
4. Properties of derivative of a function
5. Solved Examples Based on Derivative of a Function
6. Summary

In this article, we will learn the properties of Derivatives of a function. This category falls under the broader category of matrices, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of three questions have been asked on this topic including one in 2014, one in 2017, and one in 2013.

Function:

$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as
$f: A \rightarrow B$ and read as $f$ is a mapping from $A$ to $B$.

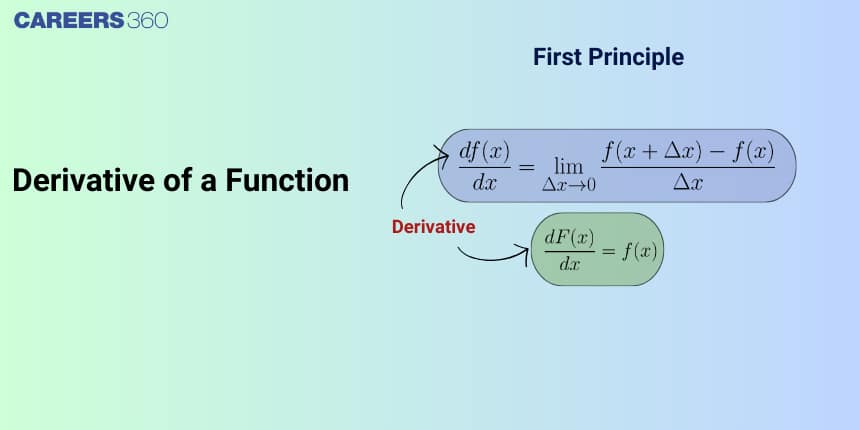
Derivative of a Function

Let $f$ be defined on an open interval $I \subseteq$ containing the point $x_0$, and suppose that $\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}$ exists. Then $f$ is said to be differentiable at $x_0$ and the derivative of $f$ at $x_0$, denoted by $f^{\prime}\left(x_0\right)$, is given by

$$
f^{\prime}\left(x_0\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}
$$

For all $x$ for which this limit exists,
$f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$ is a function of $x$.

In addition to $f^{\prime}(x)$, other notations are used to denote the derivative of $y=f(x)$. The most common notations are $f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d}{d x}[f(x)], D_x[y]$ or $D y$ or $y_1$. Here $\frac{d}{d x}$ or $D$ is the differential operator.

Derivatives of some basic functions

1. $\frac{d}{d x}($ constant $)=0$

2. $\frac{d}{d x}\left(\mathbf{x}^{\mathbf{n}}\right)=\mathbf{n} \mathbf{x}^{\mathbf{n}-1}$

3. $\frac{d}{d x}\left(\mathbf{a}^{\mathrm{x}}\right)=\mathbf{a}^{\mathrm{x}} \log _{\mathrm{e}} \mathbf{a}$

4. $\quad \frac{d}{d x}\left(\mathrm{e}^{\mathrm{x}}\right)=\mathrm{e}^{\mathrm{x}} \log _{\mathrm{e}} \mathrm{e}=\mathrm{e}^{\mathrm{x}}$

5. $\frac{d}{d x}\left(\log _{\mathrm{e}}|\mathbf{x}|\right)=\frac{\mathbf{1}}{\mathbf{x}}, \quad \mathbf{x} \neq 0$

6. $\quad \frac{d}{d x}\left(\log _{\mathbf{a}}|\mathbf{x}|\right)=\frac{1}{\mathbf{x} \log _{\mathrm{e}} \mathbf{a}}, \quad \mathbf{x} \neq 0$

7. $\frac{d}{d x}(\sin (\mathbf{x}))=\cos (\mathbf{x})$

8. $\frac{d}{d x}(\cos (\mathbf{x}))=-\sin (\mathbf{x})$

9. $\frac{d}{d x}(\tan (\mathbf{x}))=\sec ^2(\mathbf{x})$

10. $\frac{d}{d x}(\cot (\mathbf{x}))=-\csc ^2(\mathbf{x})$

11. $\frac{d}{d x}(\sec (\mathbf{x}))=\sec (\mathbf{x}) \tan (\mathbf{x})$

12. $\frac{d}{d x}(\csc (\mathbf{x}))=-\csc (\mathbf{x}) \cot (\mathbf{x})$

Higher Order Derivative of a Function

The derivative of a function is itself a function, so we can find the derivative of a derivative. The new function obtained by differentiating the derivative is called the second derivative. Furthermore, we can continue to take derivatives to obtain the third derivative, a fourth derivative, and so on.

Collectively, these are referred to as higher-order derivatives. The notation for the higher-order derivatives of $y=f(x)$ can be expressed in any of the following forms:

$
\begin{aligned}
& f^{\prime}(x), f^{\prime \prime}(x), f^{\prime \prime \prime}(x), f^{(4)}(x), \ldots, f^{(n)}(x) \\
& y^{\prime}, y^{\prime \prime}(x), y^{\prime \prime \prime}(x), y^{(4)}(x), \ldots, y^{(n)}(x) \\
& \frac{d y}{d x}, \frac{d^2 y}{d x^2}, \frac{d^3 y}{d x^3}, \frac{d^4 y}{d x^4}, \ldots, \frac{d^n y}{d x^n}
\end{aligned}
$

Properties of derivative of a function

1. The derivative of sum of two functions is equal to the sum of their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

2. The derivative of differnce betweeen two functions is equal to the difference between their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

3. The derivative of the product of two functions is given by

$\frac{d}{dx}[f(x)g(x)] = (\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))$

4. The derivative of the quotient of two functions is given by

$\frac{d}{dx}[\frac{f(x)}{g(x)}] = \frac{(\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))}{(g(x))^2}$

Recommended Video Based on Derivative of a Function

Solved Examples Based on Derivative of a Function

Example 1: If $\sin y+e^{-x \cos y}=e$, then $\frac{d y}{d x}$ at $(1, \pi)$ is ?
1) $\sin y$
2) $-x \cos y$
3) $e$
4) $\sin y-x \cos y$

Solution:

$\begin{aligned} & \quad \sin y+e^{-x \cos y}=e \\ & \text { differentiate with respect to } \mathrm{x} \\ & \cos y \frac{d y}{d x}+e^{-x \cos y}\left\{(-x)\left(-\sin y \frac{d y}{d x}\right)+\cos y(-1)\right\}=0 \\ & \cos y \frac{d y}{d x}+x \sin y e^{-x \cos y} \frac{d y}{d x}-\cos y e^{-x \cos y}=0 \\ & \frac{d y}{d x}=\frac{\cos y e^{-x \cos y}}{\cos y+x \sin y e^{-x \cos y}} \\ & \left.\frac{d y}{d x}\right|_{(1, \pi)}=\frac{\cos \pi e^{-\cos \pi}}{\cos \pi+\sin \pi e^{-\cos \pi}}=\frac{-1 \times e}{-1+0}=e\end{aligned}$

Hence, the answer is the option (3).

Example 2: If $f\left(\frac{x+y}{3}\right)=\frac{2+f(x)+f(y)}{3}$ for all real x and y and $f^{\prime}(0)=2$, then determine $\mathrm{f}(\mathrm{x})$
1) $2 x+2$
2) $2 x+3$
3) $2 x-2$
4) $3 x+2$

Solution:

Given equation is $f\left(\frac{x+y}{3}\right)=\frac{2+f(x)+f(y)}{3}$
Putting $x=0, y=0$ in $(i)$, we have,

$
3 f(0)=2+2 f(0) \Rightarrow f(0)=2
$
Putting $y=0$ and $f(0)=2$ in (i), we have,

$
f\left(\frac{x}{3}\right)=\frac{1}{3}[f(x)+4] \quad \Rightarrow f(x)=3 f\left(\frac{x}{2}\right)-4
$
Now,
$
\begin{aligned}
f^{\prime}(x) & =\lim\limits _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \\
& =\lim\limits _{h \rightarrow 0} \frac{f\left(\frac{3 x+3 h}{3}\right)-f(x)}{h} \\
& =\lim\limits _{h \rightarrow 0} \frac{\frac{f(3 x)+f(3 h)+2}{3}-f(x)}{h}
\end{aligned}
$
$
\begin{aligned}
& =\lim\limits _{h \rightarrow 0} \frac{f(3 x)+f(3 h)+2-3 f(x)}{3 h} \\
& =\lim\limits _{h \rightarrow 0} \frac{3 f(x)-4+f(3 h)-3 f(x)}{3 h} \quad\left[\text { using (ii)] } f^{\prime}(x)=2\right. \\
& \text { Integrating } \\
& f(x)=2 x+c \\
& U \text { sing } f(0)=2 \\
& f(x)=2 x+2
\end{aligned}
$

Hence, the answer is the option 1.

Example 3: Find the function $f(x)$ which is differentiable and satisfies the relation $f(x+y)=f(x)+f(y)+\left(e^x-1\right)\left(e^y-1\right) \forall x, y \in R$ and $f^{\prime}(0)=2$
1) $f(x)=e^x+x+1$
2) $f(x)=e^x+x$
3) $f(x)=e^x+x-1$
4) None of these

Solution:
$
f(x+y)=f(x)+f(y)+\left(e^x-1\right)\left(e^y-1\right) \forall x, y \in R
$

differentiate w.r.t $x$ , keeping $y$ as constant, we get

$
\begin{aligned}
& f^{\prime}(x+y)=f^{\prime}(x)+e^x\left(e^y-1\right) \\
& \text { put } \mathrm{x}=0 \\
& f^{\prime}(y)=f^{\prime}(0)+\left(e^y-1\right) \\
& f^{\prime}(y)=2+e^y-1 \\
& f(y)=e^y+y+c
\end{aligned}
$
Now put $x=y=0$ in original equation

$
\begin{aligned}
& f(0)=f(0)+f(0)+0 \\
& f(0)=0 \\
& \text { put } y=0 \text { in } f(y)=e^y+y+c \\
& c=-1 \\
& f(x)=e^x+x-1
\end{aligned}
$

Hence, the answer is the option 3.

Example 4: $f(x)$ and $g(x)$ are two differentiable functions on $[0,2]$ such that $f^{\prime \prime}(x)-g^{\prime \prime}(x)=0$, $f^{\prime}(1)=2 g^{\prime}(1)=4, f(2)=3 g(2)=9$ then $f(x)-g(x)$ at $x=\frac{3}{2}$ is:
1) $0$
2) $2$
3) $10$
4) $5$

Solution:

Given $f^{\prime \prime}(x)-g^{\prime \prime}(x)=0$

$
f^{\prime \prime}(x)=g^{\prime \prime}(x)
$
Integrating both sides, we get:

$
\begin{aligned}
& f^{\prime}(x)+C_1=g^{\prime}(x)+C_2 \\
& f^{\prime}(x)-g^{\prime}(x)=C_2-C_1
\end{aligned}
$
But $f^{\prime}(1)=2 g^{\prime}(1)=4$

$
f^{\prime}(1)=4 \text { and } g^{\prime}(1)=2
$

Therefore at $x = 1$

$\begin{aligned} & C_2-C_1=f^{\prime}(1)-g^{\prime}(1) \\ & C_2-C_1=2 f^{\prime}(x)=g^{\prime}(x)+2\end{aligned}$

Equation (1) becomes:

$
\begin{aligned}
& f^{\prime}(x)-g^{\prime}(x)=2 \\
& f^{\prime}(x)=2+g^{\prime}(x)
\end{aligned}
$
Again integrate both sides

$
\begin{aligned}
& f(x)+K_1=g(x)+K_2+2 x \\
& f(x)-g(x)=K_2-K_1+2 x
\end{aligned}
$
Since $f(2)=3 g(2)=9$
Therefore at $\mathrm{x}=2$

$
\begin{aligned}
& f(2)-g(2)=2 \times 2+\left(k_2-k_1\right) \\
& 9-3=4+\left(k_2-k_1\right) \\
& 2=\left(k_2-k_1\right)
\end{aligned}
$
Using Equation (2)

$
f(x)-g(x)=3+2=5
$

Hence, the correct option is option (4).

Example 5: A function $f: R \rightarrow R$ satisfies

$
\sin x \cos y(f(2 x+2 y))-f(2 x-2 y)=\cos x \sin y(f(2 x+2 y)+f(2 x-2 y))
$
If $f^{\prime}(0)=1 / 2$, then :
1) $f^{\prime \prime}(x)=f(x)=0$
2) $4 f^{\prime \prime}(x)+f(x)=0$
3) $f^{\prime \prime}(x)+f(x)=0$
4) $4 f^{\prime \prime}(x)-f(x)=0$

Solution:

Trigonometric functions -

$\begin{aligned} & \frac{d}{d x}(\sin x)=\cos x \\ & \frac{d}{d x}(\sec x)=\sec x \tan x \\ & \frac{d}{d x}(\operatorname{cosec} f(x))=-\operatorname{cosec}\{f(x)\} \cot \{f(x)\} f^{\prime}(x) \\ & \frac{f(2 x+2 y)}{f(2 x-2 y)}=\frac{\sin (x+y)}{\sin (x-y)} \\ & \frac{f(\alpha)}{\sin (\alpha / 2)}=\frac{f(\beta)}{\sin \beta / 2}=\mathrm{k} \\ & f(x)=k \sin x / 2 \\ & \quad f^{\prime}(x)=k / 2 \cos x / 2 \quad f^{\prime \prime}(x)=-k / 4 \sin x / 2 \\ & 4 f^{\prime \prime}(x)+f(x)=0\end{aligned}$

Hence, the answer is the option (2).

Summary

The differentiated part of the function is called the derivative of the function.Understanding of differentiation of functions is fundamental in calculus as it lays the groundwork for more complex structures and analyses. This helps in a lot of applications that are used in our day-to-day life. It has applications in various fields of study like Physics,Engineering, Medical, Architecture etc.