Shortest Distance between Two Lines in 3D Space

A line is one dimensional figure, which has length but no width. Two lines can have the following relation parallel line, perpendicular line, skewed line, and Intersecting line. Distance between two lines can be obtained by first finding the relation between lines. In real life, everything around is based on lines.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Shortest Distance between Two Lines
2. Relations Between Two Lines
3. Shortest Distance between two skew lines
4. Distance between Intersecting lines
5. Shortest Distance between parallel lines
6. Derivation of Shortest Distance between parallel lines
7. Solved Examples Based on the Shortest Distance between Two Lines

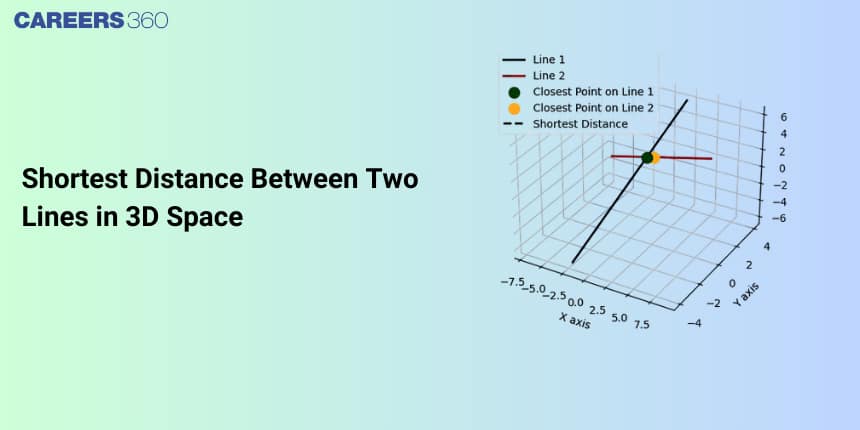
In this article, we will cover the concept of the Shortest Distance Between Two Lines. This topic falls under the broader category of three-dimensional geometry, which is a crucial chapter in Class 12 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of eleven questions have been asked on this topic in JEE Main from 2013 to 2023 including two in 2015, one in 2016, one in 2017, two in 2020, four in 2021, five in 2022, and twelve in 2023.

Shortest Distance between Two Lines

The shortest distance between two lines in three-dimensional space is the length of the perpendicular segment drawn from a point on one line to the other line. Based on the relation between two lines we can find the distance between two lines.

Relations Between Two Lines

There are three possible types of relations that two different lines can have in a three-dimensional space. They can be

1. Parallel lines: when their direction vectors are parallel and the two lines never meet.

2. Intersecting lines: when their direction vectors are not parallel and the two lines intersect.

3. Skew lines: When two lines are neither parallel nor intersecting at a point.

4. Perpendicular line: when their direction ratios are perpendicular to each other.

For example, consider a cuboid

Edges $A B$ and $C D$ are parallel. Edges $A B$ and $B C$ intersect at a single point $B$. Edges $A B$ and $E H$ are skewed since they are not parallel and never meet.

For skew lines, the line of the shortest distance will be perpendicular to both lines.

So, the shortest distance between edges $A B$ and $E H$ is $|A E|$.

Shortest Distance between two skew lines

When two lines are neither parallel nor intersecting at a point they are referred to as Skew Lines.

If $\vec{r}=\vec{a}+\lambda \vec{b}$ and $\vec{r}=\overrightarrow{a_1}+\mu \vec{b}$ are skew lines then the shortest distance between them is given by

$
\left|\frac{\left(\vec{b} \times \overrightarrow{b_1}\right) \cdot\left(\vec{a}-\overrightarrow{a_1}\right)}{\left|\vec{b} \times \overrightarrow{b_1}\right|}\right|
$

Derivation of Distance between two skew lines

If $L_1$ and $L_2$ are two skew lines, then there is one and only one line perpendicular to each of lines L1 and L2 which is known as the line of shortest distance.

Vector form
$\mathrm{L}_1: \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+\lambda \overrightarrow{\mathbf{b}}$
$\mathrm{L}_2: \quad \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}_0^{\prime}}+\mu \overrightarrow{\mathbf{b}^{\prime}}$
Let $S$ be any point on the line $L_1$ with position vector $\overrightarrow{\mathbf{r}}_0$ and $T$ on $L_2$ with position vector $\overrightarrow{\mathbf{r}}_0$. Then the magnitude of the shortest distance vector will be equal to that of the projection of ST along the direction of the line of shortest distance.

If $\overrightarrow{P Q}$ is the shortest distance vector between $\mathrm{L}_1$ and $\mathrm{L}_2$, then it is perpendicular to both $\overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{b}^{\prime}}$, therefore, the unit vector $\hat{\mathbf{n}}$ along $\overrightarrow{P Q}$ would be

$
\hat{\mathbf{n}}=\frac{\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{b}^{\prime}}}{\left|\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{b}^{\prime}}\right|}
$

Then,

$
\overrightarrow{P Q}=d \hat{\mathbf{n}}
$

where "d" is the magnitude of the shortest distance vector. Let $\theta$ be the angle between $\overrightarrow{S T}$ and $\overrightarrow{P Q}$

Then

$
\mathrm{PQ}=\mathrm{ST}|\cos \theta|
$

but,

$
\begin{aligned}
& \cos \theta=\left|\frac{\overrightarrow{\mathrm{PQ}} \cdot \overrightarrow{\mathrm{ST}}}{|\overrightarrow{\mathrm{PQ}} \| \overrightarrow{\mathrm{ST}}|}\right| \\
& =\left|\frac{d \hat{n} \cdot\left({\overrightarrow{r^{\prime}}}_0-\vec{r}_0\right)}{d \mathrm{ST}}\right| \quad\left(\text { since } \overrightarrow{\mathrm{ST}}=\vec{r}_0^{\prime}-\vec{r}_0\right) \\
& =\left|\frac{\left(\vec{b} \times \overrightarrow{b^{\prime}}\right) \cdot\left({\overrightarrow{r^{\prime}}}_0-\vec{r}_0\right)}{\mathrm{ST}\left|\vec{b} \times \overrightarrow{b^{\prime}}\right|}\right|
\end{aligned}
$

Hence, the required shortest distance is

$
d=\mathrm{PQ}=\mathrm{ST}|\cos \theta|
$

or $\quad \mathbf{d}=\left|\frac{\left(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{b}^{\prime}}\right) \cdot\left({\overrightarrow{r^{\prime}}}_0-\overrightarrow{\mathbf{r}}_0\right)}{\left|\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{b}^{\prime}}\right|}\right|$

Distance between Intersecting lines

The shortest distance between intersecting lines is 0

Vector form

$\left(\vec{b} \times \overrightarrow{b_1}\right) \cdot\left(\overrightarrow{\mathbf{r}}_0^{\prime}-\overrightarrow{\mathbf{r}}_0\right)=0$

Shortest Distance between parallel lines

If the direction vectors of two lines are parallel and the two lines never meet they are referred as Parallel Lines.

If $\vec{r}=\overrightarrow{p_1}+\lambda \vec{\nu}$ and $\vec{r}=\overrightarrow{p_2}+\mu \vec{\nu}$ are Parallel Lines then the shortest distance between them is given by

$
\frac{\left|\left(\overrightarrow{p_2}-\overrightarrow{p_1}\right) \times \vec{\nu}\right|}{|\vec{\nu}|}
$

Derivation of Shortest Distance between parallel lines

Let two lines $ L_1$ and $L_2$ be parallel. Let the equation of lines be given by

$\mathrm{L}_1: \quad \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+\lambda \overrightarrow{\mathbf{b}}$
$\mathrm{L}_2: \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+\mu \overrightarrow{\mathbf{b}}$
where, $\overrightarrow{\mathbf{r}}_0$ is the position vector of a point $S$ on $L_1$ and $\overrightarrow{\mathbf{r}_0} 0$ is the position vector of a point $T$ on $\mathrm{L}_2$.

Let $\theta$ be the angle between the vectors $S T$ and $\overrightarrow{\mathbf{b}}$.

$\begin{aligned}
&\text { Then, }\\
&\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathrm{ST}}=(|\overrightarrow{\mathbf{b}}||\overrightarrow{\mathrm{ST}}| \sin \theta)) \hat{\mathbf{n}}
\end{aligned}$

where $\hat{\mathbf{n}}$ is the unit vector perpendicular to the plane of the lines $L_1$ and $L_2$ but

$\begin{array}{ccc}
& \overrightarrow{S T}=\overrightarrow{\mathbf{r}}_0^{\prime}-\overrightarrow{\mathbf{r}}_0 \\
\Rightarrow & \overrightarrow{\mathbf{b}} \times\left(\overrightarrow{\mathbf{r}}_0-\overrightarrow{\mathbf{r}}_0\right)=(|\overrightarrow{\mathbf{b}}||\overrightarrow{\mathrm{PT}}|) \hat{\mathbf{n}} & \text { (since PT }=\mathrm{ST} \sin \theta) \\
\text { i.e. } & \left|\overrightarrow{\mathbf{b}} \times\left(\overrightarrow{\mathbf{r}}_0^{\prime}-\overrightarrow{\mathbf{r}}_0\right)\right|=(|\overrightarrow{\mathbf{b}}||\overrightarrow{\mathrm{PT}}|) \cdot 1 & \text { (as }|\hat{\mathbf{n}}|=1)
\end{array}$
Hence, the distance between the given parallel lines is
$\mathbf{d}=|\overrightarrow{\mathbf{P T}}|=\left|\frac{\overrightarrow{\mathbf{b}} \times\left(\overrightarrow{\mathbf{r}}_0^{\prime}-\overrightarrow{\mathbf{r}}_0\right)}{|\overrightarrow{\mathrm{b}}|}\right|$

Recommended Video Based on the Shortest Distance Between Two Lines

Solved Examples Based on the Shortest Distance between Two Lines

Example 1: The line $l_1$ passes through the point $(2,6,2)$ and is perpendicular to the plane $2 x+y-2 z=10$. Then the shortest distance between the line $l_1$ and the line $\frac{x+1}{2}=\frac{y+4}{-3}=\frac{z}{2}$ is :
[JEE MAINS 2023]

Solution
equation of $l_1$ is $\frac{x-2}{2}=\frac{y-6}{1}=\frac{z-2}{-2}$
Let $l_2$ is $\frac{x+1}{2}=\frac{y+4}{-3}=\frac{z}{2}$
Point on $l_1$ is $\mathrm{a}=(2,6,2)$, direction $\overrightarrow{\mathrm{p}}=\langle 2,1,-2\rangle$
Point on $l_2$ is $\mathrm{b}=(-1,-4,0)$ direction $\overrightarrow{\mathrm{q}}=\langle 2,-3,2\rangle$

The shortest distance between $l_1$ and $l_2$

$
l_2=\left|\frac{(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}) \cdot(\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{q}})}{|\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{q}}|}\right|
$
$
\begin{aligned}
\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{q}} & =\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \mathrm{k} \\
2 & 1 & -2 \\
2 & -3 & 2
\end{array}\right|=\hat{\mathrm{i}}(-4)-\hat{\mathrm{j}}(8)+\mathrm{k}(-8) \\
& =\left|\frac{\langle 3,10,2\rangle \cdot\langle-4,-8,-8\rangle}{\sqrt{16+64+64}}\right| \\
& =\left|\frac{-12-80-16}{\sqrt{144}}\right| \\
& =\frac{108}{12} \\
& =9
\end{aligned}
$

Hence, the answer is 9

Example 2: The shortest distance between the lines $\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-6}{2}$ and $\frac{x-6}{3}=\frac{1-y}{2}=\frac{z+8}{0}$ is equal to [JEE MAINS 2023]

$\begin{aligned}
&\text { Solution }\\
&\begin{gathered}
\mathrm{L}_1: \overline{\mathrm{a}}=<2,-1,6>\quad \mathrm{L}_2: \overline{\mathrm{b}}=<6,1,-8> \\
\overline{\mathrm{p}}=<3,2,2>\quad \overline{\mathrm{q}}=<3,-2,0> \\
\overline{\mathrm{p}} \times \overline{\mathrm{q}}=\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
3 & 2 & 2 \\
3 & -2 & 0
\end{array}\right|=\langle 4,6,-12> \\
=\langle 2,3,-6> \\
\mathrm{b} \Delta=\left|\frac{(\overline{\mathrm{b}}-\overline{\mathrm{a}}) \cdot|\overline{\mathrm{p}} \times \overline{\mathrm{q}}|}{|\overline{\mathrm{p}} \times \overline{\mathrm{q}}|}\right| \\
=\left|\frac{(4 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-14 \hat{\mathrm{k}}) \cdot(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-6 \hat{\mathrm{k}})}{\sqrt{4+9+36}}\right| \\
=\left|\frac{8+6+84}{\sqrt{40}}\right|=\left|\frac{98}{7}\right|=14
\end{gathered}\\
&\text { }
\end{aligned}$
Hence, the answer is 14

Example 3: The shortest distance between the lines $\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-0}{-3}$ and $\frac{x-1}{2}=\frac{y+8}{-7}=\frac{z-4}{5}$
[JEE MAINS 2023]

Solution

$
\begin{aligned}
& L_1=\frac{x-1}{2}=\frac{\mathrm{y}+8}{-7}=\frac{\mathrm{z}-4}{5}=\lambda \\
& \mathrm{L}_2 \frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}-2}{1}=\frac{\mathrm{z}-6}{-3}=\mu
\end{aligned}
$

S.D. $=\left|\frac{(\vec{b}-\vec{a}) .\left(\vec{b}_1 \times \vec{b}_2\right)}{\left|\vec{b}_1 \times \vec{b}_2\right|}\right| \begin{aligned} & \vec{a}=i-8 j+4 k \\ & \vec{b}=i+2 j+6 k\end{aligned}$

$
\begin{aligned}
& \overrightarrow{\mathrm{b}}_1 \times \overrightarrow{\mathrm{b}}_2=\left|\begin{array}{ccc}
\mathrm{i} & \mathrm{j} & \mathrm{k} \\
2 & -7 & 5 \\
2 & 1 & -3
\end{array}\right| \\
& =i(21-5)-j(-6-10)+k(2+14) \\
& =16 i+16 j+16 k \\
& \left|\vec{b}_1 \times \vec{b}_2\right|=|16(\mathrm{i}+\mathrm{j}+\mathrm{k})|
\end{aligned}
$
$
\begin{aligned}
& =16 \times \sqrt{3} \\
& \vec{b}-\vec{a}=(10 j+2 k) \\
& \text { S.D. }=\left|\frac{(10 \mathrm{j}+2 \mathrm{k}) \cdot 16(\mathrm{i}+\mathrm{j}+\mathrm{k})}{16 \sqrt{3}}\right| \\
& =\left|\frac{16(10+2)}{16 \sqrt{3}}\right|=\frac{12}{\sqrt{3}} \Rightarrow \frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\
& =\frac{12 \sqrt{3}}{3}=4 \sqrt{3}
\end{aligned}
$
Hence, the answer is $4 \sqrt{3}$

Eyample 4: The shortest distance between the lines $\frac{x+2}{1}=\frac{y}{-2}=\frac{z-5}{2}$ and $\frac{x-4}{1}=\frac{y-1}{2}=\frac{z+3}{0}$ is:
[JEE MAINS 2023]

$\begin{aligned}
&\frac{x+2}{1}=\frac{y}{-2}=\frac{z-5}{2} \quad \text { and } \quad \frac{x-4}{1}=\frac{y-1}{2}=\frac{z+3}{0}\\
\end{aligned}$

$=\frac{\left\lvert\, \begin{array}{ccc}a_2-a_1 & b_2-b_1 & c_2-c_1 \\ l_1 & m_1 & n_1 \\ l_2 & m_2 & n_2\end{array}\right. \|}{\left\|\begin{array}{ccc}\hat{\mathrm{i}} & \hat{\mathrm{j}} & \mathrm{k} \\ \mathrm{l}_1 & \mathrm{~m}_1 & \mathrm{n}_1 \\ \mathrm{l}_2 & \mathrm{~m}_2 & \mathrm{n}_2\end{array}\right\|}$
$=\left[\begin{array}{ccc}4+2 & 1-0 & -3-5 \\ 1 & -2 & 2 \\ 1 & 2 & 0\end{array}\right]$
$=\left[\begin{array}{ccc}\hat{\imath} & \hat{\jmath} & -k \\ 1 & -2 & 2 \\ 1 & 2 & 0\end{array}\right]$
$=\left[\begin{array}{ccc}6 & 1 & -8 \\ 1 & -2 & 2 \\ 1 & 2 & 0\end{array}\right]$
$=\frac{|-54|}{|-4 \hat{i}+2 \hat{j}+4 k|}$
$=\frac{54}{\sqrt{16+4+16}}$
$=\frac{54}{6}$
$=9$
Hence, the answer is 9

Eyample 5: If the shortest distance between the lines $\frac{x+\sqrt{6}}{2}=\frac{y-\sqrt{6}}{3}=\frac{z-\sqrt{6}}{4}$ and $\frac{x-\lambda}{3}=\frac{y-2 \sqrt{6}}{4}=\frac{z+2 \sqrt{6}}{5}$ is 6 , then the square of the sum of all possible values of $\lambda$ is [JEE MAINS 2023]

Solution

$
\begin{aligned}
& \mathrm{P}(-\sqrt{6}, \sqrt{6}, \sqrt{6}) \quad \mathrm{Q}(\lambda, 2 \sqrt{6},-2 \sqrt{6}) \\
& \overline{\mathrm{n}}_1=(2,3,4) \quad \overline{\mathrm{n}}_2=(3,4,5) \\
& \overline{\mathrm{n}}_1 \times \overline{\mathrm{n}}_2 \Rightarrow\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
2 & 3 & 4 \\
3 & 4 & 5
\end{array}\right|=\hat{\mathrm{i}}(-1)-\hat{\mathrm{j}}(-2)+\hat{k}(-1) \\
& =(-1,2,-1) \\
& \therefore \mathrm{S}_{\mathrm{d}}\left|\frac{\overline{\mathrm{PQ}} \cdot(-1,2,-1)}{\sqrt{6}}\right|=\frac{(\lambda+\sqrt{6}, \sqrt{6},-3 \sqrt{6}) \cdot(-1,2,-1)}{\sqrt{6}} \\
& =\left|\frac{-\lambda-\sqrt{6}+2 \sqrt{6}+3 \sqrt{6}}{\sqrt{6}}\right|=6 \\
& \Rightarrow|-\lambda+4 \sqrt{6}|=6 \sqrt{6} \\
& (+)-\lambda+4 \sqrt{6}=6 \sqrt{6} \\
& (-) \lambda-4 \sqrt{6}=6 \sqrt{6} \\
& \lambda=-2 \sqrt{6} \\
& \lambda=10 \sqrt{6} \\
& \therefore(8 \sqrt{6})^2=384
\end{aligned}
$

Summary

The shortest distance between two lines in three-dimensional space is the length of the perpendicular segment drawn from a point on one line to the other line. Based on the relation between two lines we can find the distance between two lines.