Acceleration Inclined Plane -Explanation and FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 05:31 PM IST

We use a lot of simple machines to move heavy loads from one point to another. One of them is an inclined plane. It is a plane surface which is set at an angle, other than a right angle, against a horizontal surface. An inclined plane is used to lift heavy loads with less force. The length of the inclined plane is always greater than the height of the inclined plane. So, the weight of the object can be moved along the inclined plane with less force. A playing slide in a park, flyovers, roads on hills and sloping ramps are inclined plane examples.

This Story also Contains

Importance Of Inclined Plane
Effect Of Incline On Forces And Acceleration
Forces Required To Calculate The Acceleration Of An Object On An Inclined Plane

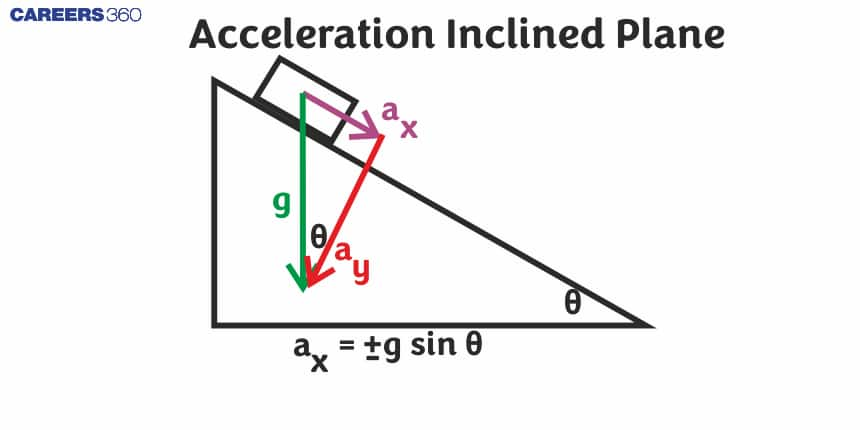
Acceleration Inclined Plane -Explanation and FAQs

Importance Of Inclined Plane

An inclined plane is a term which is used in Physics to describe a tilted surface. When we place an object on a tilted surface, it will slide down the surface. Objects placed on an inclined plane accelerate because of unbalanced forces. Whenever we place an object on the inclined plane, there are always two forces acting on it.

The normal force acts in a direction perpendicular to the surface it is acting on and the force of gravity acts in a downward direction.

Effect Of Incline On Forces And Acceleration

Acceleration plays an important role in the field of science. The rate of change of the velocity of an object with time is called acceleration and it is a vector quantity. So, it has magnitude and direction.

The force of gravity is not perpendicular to the surface in the case of an incline. As an incline angle increases, the normal force and the force of friction decrease while the force of gravity remains the same.
So, net force and acceleration increase as the incline angle increases.

Forces Required To Calculate The Acceleration Of An Object On An Inclined Plane

The free-body diagram of an object on an inclined plane is shown in the figure given below:

First of all, we need to identify the mass of the object, the coefficient of friction and the angle of the inclined plane. Then we have to calculate the following forces which act on an object which is placed on an inclined plane.

The Force Of Gravity: This force is the mass times the acceleration of gravity. As we can see from the above diagram, this force is acting in a downward direction and its value is mg

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

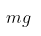
As we can see from the above figure, there are two components of this force which are mgcos\theta and mgsin\theta

Where g is the gravitational acceleration and m is the mass of the object.

Normal Force: As we can see from the above diagram, the normal force is acting perpendicular to the direction of the inclined plane. This normal force is denoted with the symbol F_{N}

Force Of Friction: The force of friction fs is acting opposite to the motion of the block which is shown with the symbol f_{s}

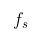
It is important to note from the above figure that the perpendicular component of the force of gravity mgcos\theta balances the normal force and the parallel component mgsin\theta and the friction force should be added together. Now, to find the net force, all the forces should be added. The net force can be defined as the vector sum of all the forces acting on the object which is placed on an inclined plane.

After calculating the net force, apply Newton’s second law which states that the net force on the object is equal to its mass times its acceleration. F_{net}=ma 1707719624337

Where a is the acceleration of the object and m is the mass of the object.

From this, we can calculate the value of the acceleration of an object on the inclined plane.

Frequently Asked Questions (FAQs)

1. Explain different types of forces.

There are two types of forces. Contact force and non-contact force. Forces which act on objects directly or through a medium are known as contact forces. Tension, normal, spring and frictional force are some examples of contact force.

Forces which act on an object without any contact are said to be non-contact forces. Non-contact forces act when there is no contact between two objects or the objects is very far away. Strong nuclear force, gravitational force and weak nuclear force are some examples of non-contact force.

2. Define positive acceleration.

If the velocity of an object is increasing with time, then we can say that the acceleration of that object is positive.

3. Define acceleration due to gravity.

The uniform acceleration produced in a freely falling object due to the gravitational force of the earth is called acceleration due to gravity.

4. What is the SI unit of force?

The SI unit of force is Newton.

5. Is force a scalar quantity?

No, force is not a scalar quantity. Force has both magnitude and direction and that is why we can say that force is a vector quantity.

6. How does acceleration on an inclined plane differ from acceleration on a flat surface?

On an inclined plane, the acceleration is less than on a flat surface because only a component of gravity acts parallel to the plane. The steeper the incline, the greater the acceleration, but it will always be less than the acceleration due to gravity (g) on a flat surface.

7. How does the normal force on an object change as the angle of the inclined plane increases?

As the angle of the inclined plane increases, the normal force decreases. This is because less of the object's weight is acting perpendicular to the plane. The normal force is given by N = mg * cos(θ), where m is the mass, g is gravity, and θ is the angle of inclination.

8. Why does an object slide down an inclined plane?

An object slides down an inclined plane because the component of its weight parallel to the plane is greater than the friction force opposing the motion. This unbalanced force causes acceleration down the plane.

9. How does the concept of resolution of forces apply to inclined plane problems?

In inclined plane problems, we resolve the weight of the object into two components: one parallel to the plane (causing acceleration) and one perpendicular to the plane (causing normal force). This allows us to analyze the forces more easily and calculate the resulting motion.

10. What is the relationship between the angle of inclination and the minimum coefficient of friction needed to prevent sliding?

The minimum coefficient of static friction (μ) needed to prevent sliding is equal to the tangent of the angle of inclination (θ). This relationship is expressed as μ = tan(θ). If the actual coefficient of friction is less than this, the object will slide.

11. What factors affect the acceleration of an object on an inclined plane?

The main factors are:

12. How is the angle of inclination related to the acceleration of an object on the plane?

As the angle of inclination increases, the acceleration of the object increases. This is because a larger component of the object's weight acts parallel to the plane, increasing the net force causing acceleration.

13. Does the mass of an object affect its acceleration down an inclined plane (ignoring friction)?

No, in the absence of friction, the mass of the object does not affect its acceleration down an inclined plane. This is because the increase in gravitational force is proportional to the increase in the object's inertia, resulting in the same acceleration for all masses.

14. How do you calculate the acceleration of an object on a frictionless inclined plane?

The acceleration (a) on a frictionless inclined plane is given by the formula: a = g * sin(θ), where g is the acceleration due to gravity (9.8 m/s²) and θ is the angle of inclination.

15. What is the role of friction in inclined plane problems?

Friction opposes the motion of an object on an inclined plane. It reduces the acceleration of objects sliding down and can prevent objects from sliding altogether if it's strong enough. The amount of friction depends on the coefficient of friction between the object and the plane.

16. What is an inclined plane in physics?

An inclined plane is a flat surface tilted at an angle to the horizontal. It's a simple machine that makes it easier to move objects up or down by spreading the work over a longer distance, reducing the force needed but increasing the distance traveled.

17. How does the work done in moving an object up an inclined plane compare to lifting it vertically?

The work done in moving an object up an inclined plane is equal to the work done in lifting it vertically to the same height. However, the inclined plane requires less force over a longer distance, while vertical lifting requires more force over a shorter distance.

18. What is the principle of mechanical advantage in relation to inclined planes?

The mechanical advantage of an inclined plane is the ratio of the weight of the object to the force parallel to the plane needed to move it. It's equal to the length of the plane divided by its height. A longer, less steep plane provides a greater mechanical advantage, requiring less force but more distance.

19. What is the significance of the critical angle in inclined plane problems?

The critical angle is the maximum angle at which an object will remain stationary on an inclined plane without sliding. It depends on the coefficient of static friction between the object and the plane. At angles greater than the critical angle, the object will begin to slide.

20. How does the concept of torque apply to objects on inclined planes?

Torque becomes relevant for extended objects on inclined planes, especially those that might tip or rotate. The torque due to gravity can cause an object to rotate if its center of mass is not directly above its point of contact with the plane. This is important in understanding the stability of objects on inclines.

21. How does the concept of energy conservation apply to an object sliding down a frictionless inclined plane?

In a frictionless inclined plane, the total energy (sum of potential and kinetic energy) remains constant. As the object slides down, its gravitational potential energy decreases while its kinetic energy increases by the same amount, conserving the total energy.

22. How does the distribution of mass in an object affect its motion on an inclined plane?

The distribution of mass affects the object's moment of inertia, which influences its rotational motion. For sliding motion, mass distribution doesn't matter. For rolling motion, objects with mass concentrated at the center (like a solid sphere) will roll faster than those with mass concentrated at the edges (like a hollow sphere).

23. What is the significance of the coefficient of restitution in collisions on inclined planes?

The coefficient of restitution determines how elastic a collision is on an inclined plane. It affects how much kinetic energy is conserved when an object bounces after hitting the plane or another object. A higher coefficient results in more elastic collisions and greater rebound.

24. How does the concept of work-energy theorem apply to inclined plane problems?

The work-energy theorem states that the work done on an object equals its change in kinetic energy. In inclined plane problems, this helps relate the work done by gravity (and other forces) to the change in the object's speed as it moves up or down the plane.

25. What is the relationship between the work done against friction and the heat generated on an inclined plane?

The work done against friction on an inclined plane is converted into heat energy. The amount of heat generated is directly proportional to the work done against friction, which depends on the coefficient of friction, the normal force, and the distance traveled along the plane.

26. How does the concept of impulse apply to collisions on inclined planes?

Impulse, the product of force and time of impact, is crucial in analyzing collisions on inclined planes. It determines the change in momentum of colliding objects. The angle of the plane affects how the impulse is resolved into components parallel and perpendicular to the plane surface.

27. How does the principle of virtual work apply to inclined plane problems?

The principle of virtual work states that the work done by applied forces equals the work done by constraint forces for any virtual displacement. In inclined plane problems, this principle can be used to analyze equilibrium conditions and solve for unknown forces, especially in complex systems involving pulleys or connected objects.

28. How does the principle of superposition apply to forces acting on objects on inclined planes?

The principle of superposition states that the net effect of multiple forces acting on an object is the vector sum of the individual forces. In inclined plane problems, this principle allows us to analyze complex situations by breaking down forces into their components and summing their effects.

29. How does the concept of virtual displacement help in solving inclined plane problems?

Virtual displacement is an imaginary, infinitesimal movement used to analyze forces in equilibrium. In inclined plane problems, it helps determine the relationship between forces without actually moving the object. This is particularly useful in applying the principle of virtual work to solve complex static equilibrium problems.

30. How does the principle of least action apply to the path of an object on a curved inclined surface?

The principle of least action states that the path taken by an object between two points is the one that minimizes the action (a quantity related to energy and time). On a curved inclined surface, this principle helps explain why objects follow specific paths, which may not always be the most obvious or direct routes.

31. What is the significance of the instantaneous axis of rotation in rolling motion on inclined planes?

The instantaneous axis of rotation is the axis about which an object rotates at any given moment. For a rolling object on an inclined plane, this axis is typically at the point of contact with the plane. Understanding this concept is crucial for analyzing the complex motion of rolling objects, including their angular velocity and acceleration.

32. How does the principle of conservation of angular momentum apply to objects rolling down inclined planes?

The conservation of angular momentum explains why a rolling object's rotational speed changes as it moves down an inclined plane. As the object descends, its moment of inertia about the axis through its center of mass remains constant, but its angular velocity increases to conserve angular momentum.

33. What is the role of the parallel axis theorem in analyzing rolling motion on inclined planes?

The parallel axis theorem relates the moment of inertia about any axis to the moment of inertia about a parallel axis through the center of mass. In inclined plane problems involving rolling motion, this theorem is useful for calculating the total kinetic energy of the object, which includes both translational and rotational components.

34. How does the concept of phase space apply to the motion of objects on inclined planes?

Phase

35. What is the difference between static and kinetic friction on an inclined plane?

Static friction prevents an object from starting to move on the inclined plane. It can vary up to a maximum value. Kinetic friction acts on an object already in motion and is typically less than the maximum static friction. It remains constant as the object moves.

36. What is the difference between uniform and non-uniform acceleration on an inclined plane?

Uniform acceleration occurs when the net force on the object remains constant, such as on a frictionless plane or when kinetic friction is constant. Non-uniform acceleration can occur when forces change, like when static friction transitions to kinetic friction or when the angle of the plane varies.

37. How does air resistance affect the motion of an object on an inclined plane?

Air resistance opposes the motion of the object, reducing its acceleration when moving down the plane and increasing the force required to move it up the plane. The effect becomes more significant at higher speeds and for objects with larger surface areas relative to their mass.

38. What is the relationship between the time taken to slide down an inclined plane and the angle of inclination?

As the angle of inclination increases, the time taken to slide down the plane decreases. This is because the component of gravity parallel to the plane increases, resulting in greater acceleration and thus less time to cover the length of the plane.

39. How does the concept of terminal velocity apply to objects on very long inclined planes?

On very long inclined planes with friction or air resistance, an object may reach terminal velocity. This occurs when the component of gravity parallel to the plane equals the sum of all resistive forces. At this point, the object continues to move at a constant velocity without further acceleration.

40. What is the difference between sliding and rolling motion on an inclined plane?

Sliding motion involves the object moving along the plane with its surface in constant contact, subject to kinetic friction. Rolling motion involves the object rotating as it moves, with only one point in contact with the plane at any instant. Rolling typically involves less energy loss due to friction.

41. What is the difference between ideal and real-world inclined plane scenarios?

Ideal inclined plane scenarios often assume frictionless surfaces and point masses, simplifying calculations. Real-world scenarios include friction, air resistance, non-uniform surfaces, and extended objects with complex shapes. These factors make real-world problems more complex but also more accurate representations of actual physical situations.

42. What is the significance of the angle of repose in inclined plane problems?

The angle of repose is the maximum angle at which a pile of granular material remains stable without sliding. In inclined plane problems, it represents the critical angle at which the static friction exactly balances the component of weight parallel to the plane, preventing motion.

43. How does the presence of fluids (like oil or water) on an inclined plane affect the motion of objects?

Fluids on an inclined plane can significantly reduce friction, often leading to hydroplaning. This can dramatically increase the acceleration of objects down the plane and make it much harder to move objects up the plane. The fluid's viscosity and the object's speed both play roles in this effect.

44. What is the significance of the center of mass in analyzing the motion of extended objects on inclined planes?

The center of mass is crucial for extended objects on inclined planes as it determines the object's overall motion. For uniform acceleration, the center of mass moves as if all the object's mass were concentrated at that point. It's also important in determining whether an object will tip over on the incline.

45. What is the role of static equilibrium in inclined plane problems?

Static equilibrium occurs when an object remains at rest on an inclined plane. It's achieved when the sum of all forces and torques acting on the object is zero. Understanding static equilibrium is crucial for determining the conditions under which an object will start to move or tip on an inclined plane.

46. How does the concept of potential energy barriers apply to objects on inclined planes?

Potential energy barriers on inclined planes represent the minimum energy an object needs to overcome to move from one position to another. This concept is important in understanding why objects might remain in certain positions on a non-uniform inclined surface, even if the overall incline would suggest movement.

47. What is the significance of the normal reaction force in inclined plane problems?

The normal reaction force is perpendicular to the inclined plane surface and balances the component of the object's weight acting perpendicular to the plane. It's crucial for calculating friction forces and determining whether an object will slide or remain stationary on the incline.

48. What is the relationship between the angle of inclination and the ratio of an object's potential energy to its kinetic energy as it slides down?

As an object slides down a frictionless inclined plane, the ratio of its potential energy to kinetic energy decreases. This ratio depends on the angle of inclination and the object's position on the plane. At the top, the ratio is infinite (all potential energy), and it approaches zero at the bottom (mostly kinetic energy).

49. How does the concept of mechanical equilibrium apply to objects on inclined planes?

Mechanical equilibrium on an inclined plane occurs when an object is either at rest or moving at constant velocity. This requires that the net force and net torque on the object are zero. Understanding mechanical equilibrium is crucial for analyzing stable configurations and threshold conditions for motion.

50. What is the significance of the parallel component of weight in inclined plane problems?

The parallel component of weight (mg * sin(θ)) is the force causing acceleration down the inclined plane. It's crucial for determining whether an object will move and, if so, how quickly. This component increases with the angle of inclination, explaining why steeper planes result in faster acceleration.

51. What is the role of the moment of inertia in the rolling motion of objects on inclined planes?

The moment of inertia affects how an object's rotational kinetic energy changes as it rolls down an inclined plane. Objects with a larger moment of inertia (like hollow cylinders) will roll down more slowly than objects with a smaller moment of inertia (like solid spheres) of the same mass and radius.

52. How does the concept of power apply to moving objects up or down an inclined plane?

Power is the rate of doing work or transferring energy. In inclined plane problems, it relates to how quickly an object is moved up the plane or how rapidly it accelerates down. The power required increases with the steepness of the incline and the speed of the object.

53. What is the significance of the angle of friction in inclined plane problems?

The angle of friction is the angle of inclination at which an object will just start to slide down the plane. It's related to the coefficient of static friction by tan(θ) = μ, where θ is the angle of friction and μ is the coefficient of static friction. This angle is crucial for determining the threshold of motion on inclined planes.

54. What is the relationship between the work done by gravity and the change in kinetic energy for an object on an inclined plane?

According to the work-energy theorem, the work done by gravity on an object moving down an inclined plane is equal to the change in its kinetic energy. This relationship holds true regardless of the presence of friction, though friction would reduce the final kinetic energy by converting some energy to heat.

55. How does the concept of constraint forces apply to objects on inclined planes?

Constraint forces, like the normal force from the inclined plane, restrict the motion of objects to specific paths. In inclined plane problems, these forces ensure that objects move along the surface of the plane rather than through it. Understanding constraint forces is crucial for correctly analyzing the dynamics of objects on inclines.