Binding Energy Per Nucleon - Overview, Structure, Properties & Uses

Q: How does the concept of binding energy per nucleon relate to Einstein's mass-energy equivalence?

Binding energy per nucleon directly applies Einstein's famous equation E=mc². The mass defect (difference between the mass of a nucleus and its constituent nucleons) is converted to binding energy using this equation, demonstrating the interchangeability of mass and energy.

Q: How does the concept of binding energy per nucleon apply to neutron stars?

In neutron stars, extreme gravitational pressure overcomes the electron degeneracy pressure, forcing electrons and protons to combine into neutrons. The binding energy per nucleon concept helps explain the stability and structure of these incredibly dense objects.

Q: What role does binding energy per nucleon play in nucleosynthesis of heavy elements?

For elements heavier than iron, which have decreasing binding energy per nucleon, energy-consuming processes like the r-process (rapid neutron capture) in supernovae are required for synthesis. Understanding binding energy helps explain why these processes are necessary for heavy element formation.

Q: How does binding energy per nucleon relate to the concept of nuclear isomers?

Nuclear isomers are excited states of nuclei with unusually long half-lives. The difference in binding energy between the ground state and the isomeric state determines the energy of the gamma ray emitted when the isomer decays, influencing its half-life and potential applications.

Q: What's the significance of binding energy per nucleon in nuclear reactor design?

In nuclear reactor design, understanding binding energy per nucleon is crucial for selecting appropriate fuel materials and predicting energy output. It helps in calculating the energy released in fission reactions and in designing efficient and safe reactor cores.

Q: Why is binding energy per nucleon important in nuclear physics?

Binding energy per nucleon is crucial because it helps us understand nuclear stability, fusion, and fission processes. It indicates how tightly bound the nucleons are within a nucleus and provides insights into which nuclear reactions are energetically favorable.

Q: How does binding energy per nucleon vary across the periodic table?

Binding energy per nucleon generally increases with atomic number up to iron-56, then gradually decreases for heavier elements. This trend explains why fusion is favorable for light elements and fission for heavy elements.

Q: Why does iron-56 have the highest binding energy per nucleon?

Iron-56 has the highest binding energy per nucleon due to the optimal balance between attractive nuclear forces and repulsive Coulomb forces. This makes it the most stable nucleus, serving as a turning point in nuclear reactions.

Q: Can binding energy per nucleon be negative?

No, binding energy per nucleon cannot be negative. A negative value would imply that energy is released when separating nucleons, which is not physically possible for stable nuclei. Binding energy is always positive, representing the energy required to break apart the nucleus.

Q: How does binding energy per nucleon relate to nuclear stability?

Higher binding energy per nucleon generally indicates greater nuclear stability. Nuclei with higher binding energies per nucleon are more tightly bound and require more energy to break apart, making them more stable.

Binding Energy Per Nucleon

Edited By Vishal kumar | Updated on Jul 02, 2025 06:59 PM IST

Binding energy per nucleon refers to the average energy that holds a nucleus together, calculated by dividing the total binding energy of the nucleus by the number of nucleons (protons and neutrons) it contains. This concept is crucial in nuclear physics as it explains the stability of different nuclei; higher binding energy per nucleon typically indicates greater stability. In real life, understanding binding energy per nucleon is essential for applications such as nuclear power generation, where energy is released by fission or fusion reactions, and in medical treatments like cancer radiotherapy. This article explores the significance of binding energy per nucleon and its practical implications in both scientific and everyday contexts, related terms to it and solved examples for better understanding.

Energy Mass Equivalence

Energy-mass equivalence, articulated by Albert Einstein in his famous equation E=mc², states that energy and mass are interchangeable; a small amount of mass can be converted into a large amount of energy and vice versa. This principle underlies many fundamental processes in physics, such as nuclear reactions, where the conversion of a tiny fraction of mass results in immense energy release.

Einstein showed from his theory of special relativity that it is necessary to treat mass as another form of energy. Einstein showed that mass is another form of energy and one can convert mass into other forms of energy, say kinetic energy and vice-versa. For this Einstein gave the famous mass-energy equivalence relation

E=mc2 where c is the velocity of light in vacuum and c=3×108 m/s

or we can say ΔE=Δmc2

where Δm= mass defect and ΔE= energy released

Note:

For a mass defect equal to 1 amu, the energy released is ΔE=(Δm)c2=(1amu)×(3×108)2=931.5MeV
A small amount of mass corresponds to a large amount of energy. Energy associated with the rest mass of an object is said to be its rest mass energy.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Rest mass of an electron (m_e)	9.1 x 10^-31 kg
Rest mass of an electron (m_e)	5.485 x 10^-4amu
Rest mass of a proton (m_p)	1.6726 x 10^-27 kg
	1.00727 amu
	1836.15 m_e
Rest mass of a neutron (m_n)	1.6749 x 10^-27 kg
Rest mass of a neutron (m_n)	1.0086 amu
Energy equivalence of rest mass of an electron	0.51 MeV
Energy equivalence of rest mass of a proton	938.27 MeV
Energy equivalence of rest mass of a neutron	939.56 MeV

It is very useful to calculate energy emitted in the nuclear process.

What is a Mass Defect?

Mass defect refers to the difference between the mass of an atomic nucleus and the sum of the masses of its protons and neutrons. This phenomenon occurs because a portion of the mass is converted into binding energy, which holds the nucleus together.

It is found that the mass of a nucleus is always less than the sum of the masses of its constituent nucleons in a free state.

This difference in masses is called the mass defect.

Hence mass defect is given as

Δm= Sum of masses of nucleons- Mass of the nucleus Δm=[Zmp+(A−Z)mn]−M
where
mp= Mass of proton, mn= Mass of each neutron,
M= Mass of nucleus, Z= Atomic number, A= Mass number,

Note- The mass of a typical nucleus is about 1% less than the sum of masses of nucleons.

What is a Packing Fraction?

Packing fraction is a concept in nuclear physics that quantifies the average binding energy per nucleon in a nucleus. It is defined as the mass defect per nucleon, expressed as a fraction of the atomic mass unit (AMU).

Mass defect per atomic mass number is called packing fraction. The packing fraction measures the stability of a nucleus. The smaller the value of the packing fraction, the larger the stability of the nucleus.

Packing fraction (f)=ΔmA=M−(Zmp+(A−Z)mn)A
mp= Mass of proton, mn= Mass of each neutron,
M= Mass of nucleus, Z= Atomic number, A= Mass number

Packing Fraction can have positive, negative, or zero values.
The zero value of the packing fraction is found in monoisotopic elements where the isotopic mass is equal to the mass number. For For 8O16f→ zero
A negative value of packing fraction indicates that there is a mass defect, hence binding energy. Such nuclei are stable.
Positive values of the Packing fraction are unstable when undergoing fission and fusion processes.

Nuclear binding energy (B.E)

Nuclear binding energy (B.E) is the energy required to disassemble a nucleus into its constituent protons and neutrons. It represents the energy released when a nucleus is formed from these nucleons and is a measure of the stability of the nucleus. The greater the binding energy, the more stable the nucleus. The neutrons and protons in a stable nucleus are held together by nuclear forces and energy is needed to pull them infinitely apart. This energy is called the binding energy of the nucleus.

The amount of energy released when nucleons come together to form a nucleus is called the binding energy of the nucleus.

The binding energy of a nucleus may be defined as the energy equivalent to the mass defect of the nucleus.

If Δm is a mass defect then according to Einstein's mass-energy relation

then

Binding energy =Δm×c2=[{mpZ+mn(A−Z)}−M]×c2J Binding energy =Δm×931.5MeV

To see how nucleon binding energy varies from nucleus to nucleus, it is important to compare the binding energy on a nucleon basis. A more useful measure of the binding between protons and neutrons is the binding energy per nucleon or E_bn. It is the ratio of the binding energy of a nucleus to the number of nucleons in the nucleus:

Ebn=EbA or Ebn=ΔMc2 A

where, A = Number of Nucleons.

We can define binding energy per nucleon theoretically as the average energy per nucleon needed to separate a nucleus into its individual nucleons.

Let’s look at a plot of the binding energy per nucleon versus the mass number for a large number of nuclei:

The following main features of the plot are

The maximum binding energy per nucleon is around 8.75 MeV for mass number (A) = 56.
The minimum binding energy per nucleon is around 7.6 MeV for mass number (A) = 238.
The binding energy per nucleon, E_bn, is practically constant, i.e. practically independent of the atomic number for nuclei of middle mass number ( 30 < A < 170).
E_bn is lower for both light nuclei (A<30) and heavy nuclei (A>170).

We can draw some conclusions from these four observations:

Conclusion 1

The force is attractive and sufficiently strong to produce a binding energy of a few MeV per nucleon.

Conclusion 2

E_bn is nearly constant in the range 30 < A < 170 because the nuclear force is short-ranged. Consider a particular nucleon inside a sufficiently large nucleus. It will be under the influence of only some of its neighbours, which come within the range of the nuclear force.
This means that all nucleons beyond the range of the nuclear force form N_A will have no influence on the binding energy of N_A. So, we can conclude that if a nucleon has ‘p’ neighbours within the range of the nuclear force, then its binding energy is proportional to ‘p’.
If we increase A by adding nucleons they will not change the binding energy of a nucleon inside. Since most of the nucleons in a large nucleus reside inside it and not on the surface, the change in binding energy per nucleon would be small.
The binding energy per nucleon is a constant and is equal to pk, where k is a constant having the dimensions of energy. Also, the property that a given nucleon influences only nucleons close to it is also referred to as the saturation property of the nuclear force.

Conclusion 3

A very heavy nucleus, say A = 240, has lower binding energy per nucleon compared to that of a nucleus with A = 120. Thus if a nucleus A = 240 breaks into two A = 120 nuclei, nucleons get more tightly bound. Also, in the process energy is released. This concept is used in Nuclear Fission.

Conclusion 4

Now consider two very light nuclei with A < 10. If these two nuclei were to join to form a heavier nucleus, then the binding energy per nucleon of the fused and heavier nucleus would be more than the E_bn of the lighter nuclei. So, the nucleons are more tightly bound post-fusion. Again energy would be released in such a process of fusion. This is the energy source of the sun.

What is Nuclear Force?

Coulomb force is a force that determines the motion of atomic electrons. As in the previous concept, we have seen that for average mass nuclei, the binding energy per nucleon is approximately 8 MeV, This is much larger than the binding energy in atoms. Hence, the nuclear force required to bind a nucleus together must be very strong and of a different type. It must be strong enough to overcome the repulsion between the (positively charged) protons and to bind both protons and neutrons into the tiny nuclear volume.

Le's look at the features of this force also called the nuclear binding force which is obtained from many experiments which were performed in between 1930 and 1950.

The nuclear force is much stronger than the Coulomb force acting between charges or the gravitational forces between masses. This is because the nuclear force needs to overpower the Coulomb repulsive force between the like-charged protons inside the nucleus. Hence, the nuclear force > the Coulomb force. Also, the gravitational force is much weaker than the Coulomb force.
The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few femtometres. This leads to a saturation of forces in a medium or a large-sized nucleus, which is the reason for the constancy of the binding energy per nucleon. Also, if the distance falls below 0.7fm, then this force becomes repulsive. A rough plot of the potential energy between two nucleons as a function of distance is shown below.

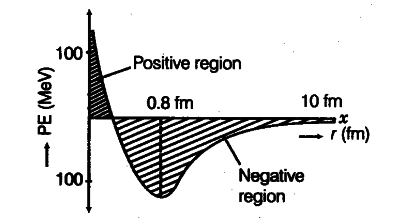
The potential energy of two nucleons is a function of the distance between them.

If distance >rα, then nuclear force = attractive
If distance <rα the nuclear force = repulsive

The nuclear force between neutron-neutron, proton-neutron and proton-proton is approximately the same. The nuclear force does not depend on the electric charge.

Nuclear Stability

Nuclear Stability is a concept that helps to identify the stability of an isotope. The two main factors that determine nuclear stability are the neutron/proton ratio (neutron to proton ratio.) and the total number of nucleons in the nucleus.

Neutron/Proton Ratio

The graph below is a plot of the number of neutrons versus the number of protons in various stable isotopes. Stable nuclei with atomic numbers up to about 20 have an n/p ratio of about 1/1.

Above Z = 20, the number of neutrons always exceeds the number of protons in stable isotopes. The stable nuclei are located in the pink band known as the belt of stability. The belt of stability ends at lead-208.

Number of Nucleons

No nucleus higher than lead-208 is stable. That's because, although the nuclear strong force is about 100 times as strong as the electrostatic repulsions, it operates over only very short distances. When a nucleus reaches a certain size, the strong force is no longer able to hold the nucleus together.

Solved Examples Based on Binding Energy Per Nucleon

Example 1: The binding energy per nucleon of deuteron (12H) and helium nucleus (24He) is 1.1 MeV and 7 MeV respectively. If two deuteron nuclei react to form a single helium nucleus, then the energy released is :

1) 13.9 MeV
2) 26.9 MeV
3) 23.6 MeV
4) 19.2 MeV

Solution:

Q value
X+Y→Z+QQ=(Mx+My−Mz)C2

where

Mx and My are mass of reactant
Mz is the mass of the product
Energy released =E(24He)−2E(12H)=(7×4−4×1.1)MeV=23.6MeV

Hence, the answer option is (3).

Example 2: When 3Li† nuclei are bombarded by protons, and the resultant nuclei are 4Be8 the emitted particles will be :

1) neutrons

2) alpha particles

3) Beta particles

4) gamma photons

Solution:

37Li+11p→48Be+zAX

From conservation of atomic number z + 4 = 4 or z = 0

From conservation of mass number 7 + 1 = 8 + A or A = 0

So the particle is a massless particle and hence it is a gamma photon.

Hence, the answer is option (4).

Example 3: Two deuterons undergo nuclear fusion to form a Helium nucleus. The energy released (in MeV ) in this process is : (given binding energy per nucleon for deuteron=1.1 MeV and for helium=7.0 MeV)

1) 23.6

2) 32.4

3) 30.2

4) 25.8

Solution:

12D+12D→24He Energy produced =−2 m(12D)+m(24He)=(4×7)−(4×1.1)=23.6MeV
Hence, the answer is option (1).

Example 4: If the binding energy per nucleon in 37Li and 24He nuclei are 5.60 MeV and 7.06 MeV respectively, then in the reaction: p+37Li→224He the energy of the proton (in MeV ) must be :

1) 17.28

2) 28.24

3) 39.2

4) 1.46

Solution:

Q value X+Y→Z+QQ=(Mx+My−Mz)C2 wherein Mx and My are mass of reactant Mz is mass of product Binding energy of 37Li=7×5.60=39.2MeV Binding energy of 24He=4×7.06=28.24MeV∴ The energy of proton = Energy of [2(24He)−37Li]=2×28.24−39.2=17.28MeV

Example 5: Find the binding energy (in MeV ) per nucleon for 50120Sn. Mass of proton mp=1.00783U, mass of neutron mn=1.00867U and mass of tin nucleus mSn=119.902199U

(take 1U = 931 MeV)

1) 8.5

2) 9.0

3) 8.0

4) 7.5

Solution:

The number of protons in 50Sn120=50 andthenumberofneutrons =120− 50=70.

=[50×1.00783u+70×1.00867u−119.902199u]c2=(1.096201u)c2=(1.096201u)(931MeV/u)=1020.563131MeV
Binding energy per nucleon =1020.563131120=8.504MeV≈8.5MeV

Hence, the answer is (8.5).

Summary

Binding energy per nucleon is a key measure of nuclear stability, indicating the average energy holding a nucleus together. Higher binding energy per nucleon generally implies greater stability, influencing nuclear reactions such as fission and fusion. Concepts like mass defect, packing fraction, and nuclear force are crucial for understanding nuclear processes and their applications in energy production and medical treatments. Solved examples illustrate practical calculations of energy release and nuclear stability in various reactions.

Frequently Asked Questions (FAQs)

1. How does the concept of binding energy per nucleon relate to Einstein's mass-energy equivalence?

Binding energy per nucleon directly applies Einstein's famous equation E=mc². The mass defect (difference between the mass of a nucleus and its constituent nucleons) is converted to binding energy using this equation, demonstrating the interchangeability of mass and energy.

2. How does the concept of binding energy per nucleon apply to neutron stars?

In neutron stars, extreme gravitational pressure overcomes the electron degeneracy pressure, forcing electrons and protons to combine into neutrons. The binding energy per nucleon concept helps explain the stability and structure of these incredibly dense objects.

3. What role does binding energy per nucleon play in nucleosynthesis of heavy elements?

For elements heavier than iron, which have decreasing binding energy per nucleon, energy-consuming processes like the r-process (rapid neutron capture) in supernovae are required for synthesis. Understanding binding energy helps explain why these processes are necessary for heavy element formation.

4. How does binding energy per nucleon relate to the concept of nuclear isomers?

Nuclear isomers are excited states of nuclei with unusually long half-lives. The difference in binding energy between the ground state and the isomeric state determines the energy of the gamma ray emitted when the isomer decays, influencing its half-life and potential applications.

5. What's the significance of binding energy per nucleon in nuclear reactor design?

In nuclear reactor design, understanding binding energy per nucleon is crucial for selecting appropriate fuel materials and predicting energy output. It helps in calculating the energy released in fission reactions and in designing efficient and safe reactor cores.

6. Why is binding energy per nucleon important in nuclear physics?

Binding energy per nucleon is crucial because it helps us understand nuclear stability, fusion, and fission processes. It indicates how tightly bound the nucleons are within a nucleus and provides insights into which nuclear reactions are energetically favorable.

7. How does binding energy per nucleon vary across the periodic table?

Binding energy per nucleon generally increases with atomic number up to iron-56, then gradually decreases for heavier elements. This trend explains why fusion is favorable for light elements and fission for heavy elements.

8. Why does iron-56 have the highest binding energy per nucleon?

Iron-56 has the highest binding energy per nucleon due to the optimal balance between attractive nuclear forces and repulsive Coulomb forces. This makes it the most stable nucleus, serving as a turning point in nuclear reactions.

9. Can binding energy per nucleon be negative?

No, binding energy per nucleon cannot be negative. A negative value would imply that energy is released when separating nucleons, which is not physically possible for stable nuclei. Binding energy is always positive, representing the energy required to break apart the nucleus.

10. How does binding energy per nucleon relate to nuclear stability?

Higher binding energy per nucleon generally indicates greater nuclear stability. Nuclei with higher binding energies per nucleon are more tightly bound and require more energy to break apart, making them more stable.

11. What is binding energy per nucleon?

Binding energy per nucleon is the average energy required to separate a single nucleon (proton or neutron) from an atomic nucleus. It represents the strength of the nuclear force holding the nucleus together and is typically measured in MeV (million electron volts).

12. Why does the binding energy per nucleon curve peak at iron-56?

The binding energy per nucleon curve peaks at iron-56 due to the optimal balance between the strong nuclear force (which is attractive and short-range) and the electromagnetic force (which is repulsive for protons). For heavier nuclei, the repulsive force begins to dominate, reducing stability.

13. How does binding energy per nucleon affect nuclear fusion reactions?

In fusion reactions, light nuclei combine to form heavier nuclei. If the product nucleus has a higher binding energy per nucleon than the reactants, energy is released. This is why fusion is energetically favorable for elements lighter than iron.

14. What role does binding energy per nucleon play in nuclear fission?

In fission reactions, heavy nuclei split into lighter nuclei. If the product nuclei have a higher average binding energy per nucleon than the original nucleus, energy is released. This is why fission is energetically favorable for elements heavier than iron.

15. How does the concept of binding energy per nucleon explain why fusion powers stars?

Stars primarily fuse hydrogen into helium, and later, helium into heavier elements. Since these light elements have lower binding energies per nucleon than the fusion products, energy is released in the process, powering the star.

16. What's the relationship between binding energy and mass defect?

Binding energy and mass defect are directly related. The mass defect is the difference between the mass of a nucleus and the sum of its constituent nucleon masses. This mass difference, when converted to energy using E=mc², gives the binding energy.

17. Can we directly measure binding energy per nucleon?

We cannot directly measure binding energy per nucleon. Instead, it's calculated from precise mass measurements of nuclei and their constituent nucleons, using the mass-energy equivalence principle (E=mc²).

18. What role does binding energy per nucleon play in the formation of elements in the universe?

Binding energy per nucleon determines which fusion reactions are energetically favorable in stars, guiding the process of nucleosynthesis. It explains why elements up to iron can be formed in stellar cores, while heavier elements require more extreme conditions like supernovae.

19. How does binding energy per nucleon affect nuclear reaction rates?

Reactions that result in nuclei with higher binding energy per nucleon are generally more likely to occur. The difference in binding energy between reactants and products influences the reaction rate and determines whether a reaction is exothermic or endothermic.

20. What's the significance of the binding energy per nucleon in nuclear medicine?

In nuclear medicine, understanding binding energy helps in selecting appropriate radioisotopes for imaging and therapy. It influences the half-life and decay properties of isotopes, which are crucial factors in medical applications.

21. How is binding energy per nucleon calculated?

Binding energy per nucleon is calculated by dividing the total binding energy of a nucleus by the number of nucleons. The total binding energy is the difference between the mass of the nucleus and the sum of its constituent nucleon masses, converted to energy using E=mc².

22. How does the liquid drop model of the nucleus relate to binding energy per nucleon?

The liquid drop model treats the nucleus as a drop of incompressible nuclear fluid. It provides a semi-empirical mass formula that helps calculate binding energies, explaining the general trend of binding energy per nucleon across the periodic table.

23. What's the significance of the binding energy per nucleon in nuclear power generation?

Understanding binding energy per nucleon is crucial for nuclear power generation. It helps in selecting appropriate fissile materials and designing efficient reactors by identifying which nuclear reactions will release the most energy.

24. How does the concept of binding energy per nucleon relate to nuclear astrophysics?

In nuclear astrophysics, binding energy per nucleon helps explain stellar nucleosynthesis, the formation of elements in stars. It determines which fusion reactions are energetically favorable and guides our understanding of stellar evolution and element formation in the universe.

25. Why can't we fuse elements heavier than iron to produce energy?

Fusing elements heavier than iron requires energy input rather than releasing energy. This is because the binding energy per nucleon decreases for elements heavier than iron, making fusion energetically unfavorable.

26. How does binding energy per nucleon affect the cosmic abundance of elements?

The cosmic abundance of elements is largely determined by their binding energies per nucleon. Elements with higher binding energies (like iron) are more stable and thus more abundant, while those with lower binding energies are rarer in the universe.

27. How does the pairing effect influence binding energy per nucleon?

The pairing effect in nuclei leads to slightly higher binding energies for nuclei with even numbers of protons or neutrons. This is due to the tendency of nucleons to form pairs, resulting in increased stability and higher binding energy per nucleon.

28. How does the concept of binding energy per nucleon help in understanding nuclear deformation?

Nuclear deformation can affect binding energy per nucleon. Deformed nuclei may have slightly different binding energies compared to spherical nuclei of the same mass number, which can be understood by considering how deformation affects the balance of nuclear and Coulomb forces.

29. How does binding energy per nucleon relate to the concept of nuclear symmetry energy?

Nuclear symmetry energy represents the energy cost of creating an imbalance between protons and neutrons in a nucleus. It's closely related to binding energy per nucleon and helps explain why heavy stable nuclei have more neutrons than protons.

30. What's the relationship between binding energy per nucleon and nuclear transmutation?

Nuclear transmutation involves changing one element into another through nuclear reactions. The difference in binding energy per nucleon between the initial and final nuclei determines whether the transmutation releases or requires energy, guiding which transmutations are practically achievable.

31. What's the significance of binding energy per nucleon in understanding the island of stability for superheavy elements?

The island of stability refers to a predicted region of superheavy elements with relatively long half-lives. Understanding binding energy per nucleon helps predict where this island might occur, as it would correspond to a local increase in nuclear binding energy and stability for very heavy nuclei.

32. How does binding energy per nucleon relate to the concept of nuclear shell model?

The nuclear shell model explains certain "magic numbers" of protons or neutrons that result in especially stable nuclei. These magic numbers correspond to peaks in the binding energy per nucleon curve, indicating increased stability.

33. How does binding energy per nucleon affect radioactive decay?

Nuclei with lower binding energies per nucleon are generally less stable and more prone to radioactive decay. The type and rate of decay depend on how the nucleus can increase its overall binding energy per nucleon.

34. Why does the binding energy per nucleon initially increase rapidly for light nuclei?

For light nuclei, each additional nucleon can interact with all others, significantly increasing the total binding energy. This leads to a rapid increase in binding energy per nucleon for the lightest elements.

35. What's the relationship between binding energy per nucleon and nuclear force?

The nuclear force is responsible for the binding energy. The strength and range of the nuclear force determine how tightly nucleons are bound together, directly affecting the binding energy per nucleon.

36. How does the proton-to-neutron ratio affect binding energy per nucleon?

The optimal proton-to-neutron ratio for maximum binding energy per nucleon varies with atomic number. For light nuclei, equal numbers of protons and neutrons are most stable, while heavier stable nuclei tend to have more neutrons than protons.

37. Why doesn't binding energy per nucleon increase indefinitely with atomic number?

Binding energy per nucleon doesn't increase indefinitely because of the growing electrostatic repulsion between protons as atomic number increases. This repulsion counteracts the attractive nuclear force, leading to a decrease in binding energy per nucleon for heavy nuclei.

38. How does binding energy per nucleon relate to the concept of nuclear drip lines?

Nuclear drip lines represent the limits of nuclear stability. Beyond these lines, the binding energy becomes negative, meaning nucleons are no longer bound to the nucleus. Understanding binding energy helps predict where these drip lines occur.

39. What's the connection between binding energy per nucleon and nuclear magic numbers?

Nuclear magic numbers correspond to particularly stable configurations of protons or neutrons. Nuclei with magic numbers of protons or neutrons show peaks in the binding energy per nucleon curve, indicating enhanced stability.

40. Why is the binding energy per nucleon curve important for understanding nuclear stability?

The binding energy per nucleon curve provides a visual representation of nuclear stability across the periodic table. Peaks in the curve indicate more stable nuclei, while troughs suggest less stable configurations, helping predict nuclear behavior and decay patterns.

41. What's the relationship between binding energy per nucleon and nuclear fission yield?

In nuclear fission, the yield (distribution of fission products) is influenced by binding energy per nucleon. Fission tends to produce fragments with higher binding energies per nucleon, as these are more energetically favorable.

42. Why is the binding energy per nucleon curve nearly flat for medium-mass nuclei?

The binding energy per nucleon curve is nearly flat for medium-mass nuclei because the attractive nuclear force and repulsive Coulomb force are in near balance. This results in a relatively constant binding energy per nucleon for a range of medium-mass elements.

43. How does binding energy per nucleon relate to the concept of nuclear saturation?

Nuclear saturation refers to the observation that the density of nucleons in a nucleus is roughly constant, regardless of the nucleus size. This is reflected in the binding energy per nucleon curve, which plateaus for medium-mass nuclei, indicating a saturation of nuclear forces.

44. What's the significance of binding energy per nucleon in understanding the limits of the periodic table?

Binding energy per nucleon helps predict the limits of the periodic table. As we move to very heavy elements, the decreasing binding energy per nucleon indicates increasing instability, setting theoretical limits on how heavy an element can be while remaining bound.

45. What's the connection between binding energy per nucleon and nuclear shell effects?

Nuclear shell effects, which lead to magic numbers, cause local fluctuations in the binding energy per nucleon curve. These effects result in certain nuclei having higher binding energies than would be expected from smooth trends, indicating enhanced stability.

46. What role does binding energy per nucleon play in understanding cosmic ray spallation?

In cosmic ray spallation, high-energy particles break apart nuclei in the upper atmosphere. Understanding binding energy per nucleon helps predict the products of these reactions and explains why certain isotopes are produced more abundantly than others.

47. How does the concept of binding energy per nucleon apply to nuclear forensics?

In nuclear forensics, binding energy per nucleon helps in identifying the origin and history of nuclear materials. It aids in determining the enrichment level of uranium samples and in analyzing debris from nuclear events to infer their nature and source.

48. How does binding energy per nucleon influence the design of nuclear weapons?

In nuclear weapons design, understanding binding energy per nucleon is crucial for selecting fissile materials and predicting yield. It determines the energy release in both fission and fusion processes, influencing the efficiency and power of the weapon.

49. What role does binding energy per nucleon play in stellar nucleosynthesis of elements beyond iron?

For elements beyond iron, which have decreasing binding energy per nucleon, stellar nucleosynthesis requires energy input. This occurs in processes like the s-process in red giants and the r-process in neutron star mergers, where the extreme conditions overcome the unfavorable energetics.

50. How does the concept of binding energy per nucleon relate to nuclear pasta in neutron star crusts?

Nuclear pasta refers to exotic nuclear structures theorized to exist in neutron star crusts. The competition between nuclear and electromagnetic forces, which determines binding energy per nucleon, leads to these unusual configurations under extreme densities and pressures.